0-2-e-tg-2-x-dx-

Question Number 184027 by SEKRET last updated on 02/Jan/23

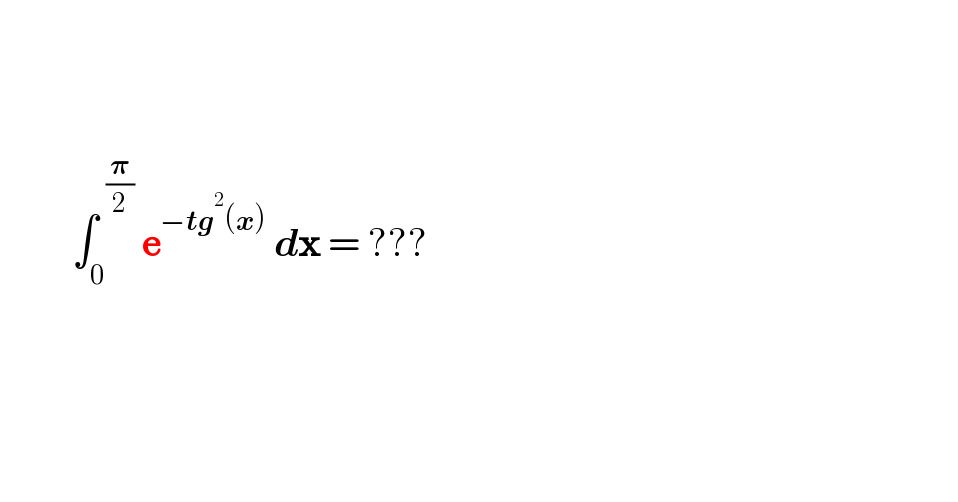
$$\:\:\: \\ $$$$ \\ $$$$ \\ $$$$\:\:\:\:\:\:\:\:\:\int_{\mathrm{0}} ^{\:\:\frac{\boldsymbol{\pi}}{\mathrm{2}}} \:\boldsymbol{\mathrm{e}}^{−\boldsymbol{{tg}}^{\mathrm{2}} \left(\boldsymbol{{x}}\right)} \:\boldsymbol{{d}\mathrm{x}}\:=\:??? \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$

Answered by witcher3 last updated on 03/Jan/23

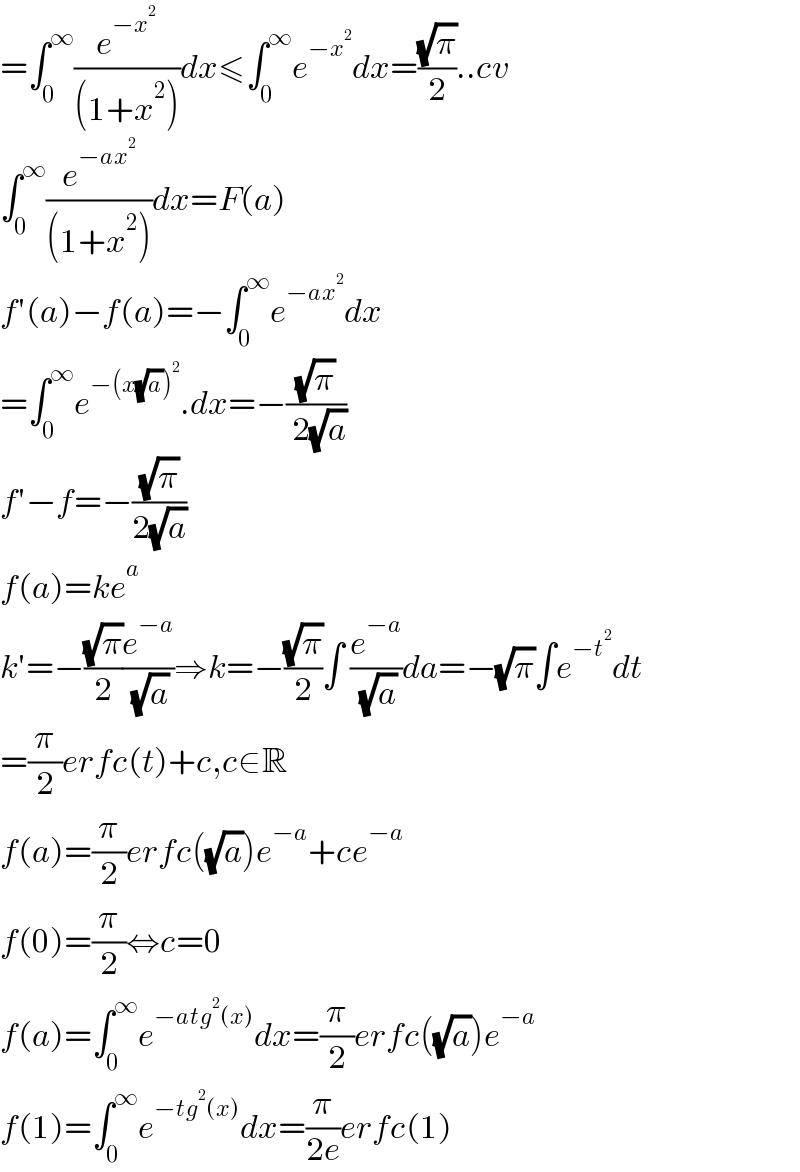
=∫_0 ^∞ (e^(−x^2 ) /((1+x^2 )))dx≤∫_0 ^∞ e^(−x^2 ) dx=((√π)/2)..cv ∫_0 ^∞ (e^(−ax^2 ) /((1+x^2 )))dx=F(a) f′(a)−f(a)=−∫_0 ^∞ e^(−ax^2 ) dx =∫_0 ^∞ e^(−(x(√a))^2 ) .dx=−((√π)/( 2(√a))) f′−f=−((√π)/(2(√a))) f(a)=ke^a k′=−((√π)/2)(e^(−a) /( (√a)))⇒k=−((√π)/2)∫ (e^(−a) /( (√a)))da=−(√π)∫e^(−t^2 ) dt =(π/2)erfc(t)+c,c∈R f(a)=(π/2)erfc((√a))e^(−a) +ce^(−a) f(0)=(π/2)⇔c=0 f(a)=∫_0 ^∞ e^(−atg^2 (x)) dx=(π/2)erfc((√a))e^(−a) f(1)=∫_0 ^∞ e^(−tg^2 (x)) dx=(π/(2e))erfc(1)

$$=\int_{\mathrm{0}} ^{\infty} \frac{{e}^{−{x}^{\mathrm{2}} } }{\left(\mathrm{1}+{x}^{\mathrm{2}} \right)}{dx}\leqslant\int_{\mathrm{0}} ^{\infty} {e}^{−{x}^{\mathrm{2}} } {dx}=\frac{\sqrt{\pi}}{\mathrm{2}}..{cv} \\ $$$$\int_{\mathrm{0}} ^{\infty} \frac{{e}^{−{ax}^{\mathrm{2}} } }{\left(\mathrm{1}+{x}^{\mathrm{2}} \right)}{dx}={F}\left({a}\right) \\ $$$${f}'\left({a}\right)−{f}\left({a}\right)=−\int_{\mathrm{0}} ^{\infty} {e}^{−{ax}^{\mathrm{2}} } {dx} \\ $$$$=\int_{\mathrm{0}} ^{\infty} {e}^{−\left({x}\sqrt{{a}}\right)^{\mathrm{2}} } .{dx}=−\frac{\sqrt{\pi}}{\:\mathrm{2}\sqrt{{a}}} \\ $$$${f}'−{f}=−\frac{\sqrt{\pi}}{\mathrm{2}\sqrt{{a}}} \\ $$$${f}\left({a}\right)={ke}^{{a}} \\ $$$${k}'=−\frac{\sqrt{\pi}}{\mathrm{2}}\frac{{e}^{−{a}} }{\:\sqrt{{a}}}\Rightarrow{k}=−\frac{\sqrt{\pi}}{\mathrm{2}}\int\:\frac{{e}^{−{a}} }{\:\sqrt{{a}}}{da}=−\sqrt{\pi}\int{e}^{−{t}^{\mathrm{2}} } {dt} \\ $$$$=\frac{\pi}{\mathrm{2}}{erfc}\left({t}\right)+{c},{c}\in\mathbb{R} \\ $$$${f}\left({a}\right)=\frac{\pi}{\mathrm{2}}{erfc}\left(\sqrt{{a}}\right){e}^{−{a}} +{ce}^{−{a}} \\ $$$${f}\left(\mathrm{0}\right)=\frac{\pi}{\mathrm{2}}\Leftrightarrow{c}=\mathrm{0} \\ $$$${f}\left({a}\right)=\int_{\mathrm{0}} ^{\infty} {e}^{−{atg}^{\mathrm{2}} \left({x}\right)} {dx}=\frac{\pi}{\mathrm{2}}{erfc}\left(\sqrt{{a}}\right){e}^{−{a}} \\ $$$${f}\left(\mathrm{1}\right)=\int_{\mathrm{0}} ^{\infty} {e}^{−{tg}^{\mathrm{2}} \left({x}\right)} {dx}=\frac{\pi}{\mathrm{2}{e}}{erfc}\left(\mathrm{1}\right) \\ $$

Commented by SEKRET last updated on 05/Jan/23

$$\boldsymbol{\mathrm{thanks}}\:\:\boldsymbol{\mathrm{sir}}.\:\boldsymbol{\mathrm{beatiful}}\:\boldsymbol{\mathrm{solution}} \\ $$

Commented by witcher3 last updated on 05/Jan/23

$${withe}\:{pleasur} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply