Question Number 62179 by Tawa1 last updated on 16/Jun/19
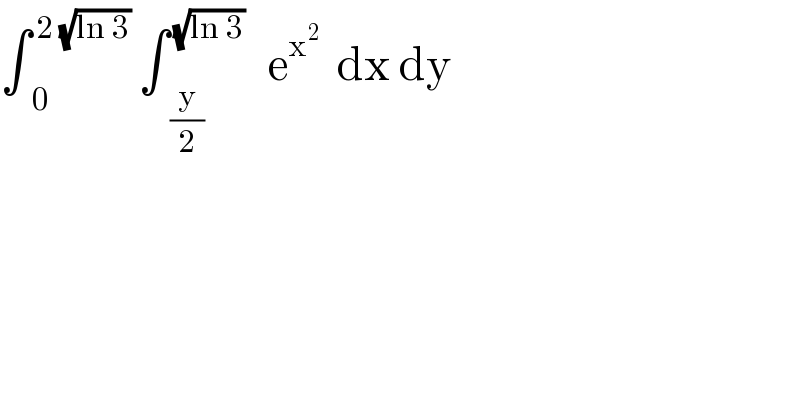
$$\int_{\:\:\mathrm{0}} ^{\:\mathrm{2}\:\sqrt{\mathrm{ln}\:\mathrm{3}}} \:\int_{\:\:\frac{\mathrm{y}}{\mathrm{2}}} ^{\:\sqrt{\mathrm{ln}\:\mathrm{3}}} \:\:\:\mathrm{e}^{\mathrm{x}^{\mathrm{2}} } \:\:\mathrm{dx}\:\mathrm{dy} \\ $$
Commented by maxmathsup by imad last updated on 17/Jun/19
![(y/2)≤x ≤(√(ln3 )) ⇒y ≤2x and x ≤(√(ln3 )) ⇒ ∫_0 ^(√(ln3)) ( ∫_0 ^(2x) dy)e^x^2 dx = ∫_0 ^(√(ln3)) 2x e^x^2 dx =[e^x^2 ]_0 ^(√(ln3)) =e^(ln(3)) −1 =3−1 =2 but its only a try....](https://www.tinkutara.com/question/Q62181.png)
$$\frac{{y}}{\mathrm{2}}\leqslant{x}\:\leqslant\sqrt{{ln}\mathrm{3}\:}\:\Rightarrow{y}\:\leqslant\mathrm{2}{x}\:\:{and}\:{x}\:\leqslant\sqrt{{ln}\mathrm{3}\:}\:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\sqrt{{ln}\mathrm{3}}} \:\:\:\left(\:\int_{\mathrm{0}} ^{\mathrm{2}{x}} \:{dy}\right){e}^{{x}^{\mathrm{2}} } {dx}\:\:=\:\int_{\mathrm{0}} ^{\sqrt{{ln}\mathrm{3}}} \:\mathrm{2}{x}\:{e}^{{x}^{\mathrm{2}} } {dx}\:=\left[{e}^{{x}^{\mathrm{2}} } \right]_{\mathrm{0}} ^{\sqrt{{ln}\mathrm{3}}} \:={e}^{{ln}\left(\mathrm{3}\right)} −\mathrm{1}\:=\mathrm{3}−\mathrm{1}\:=\mathrm{2} \\ $$$${but}\:{its}\:{only}\:{a}\:{try}…. \\ $$
