Question Number 189874 by mathocean1 last updated on 23/Mar/23
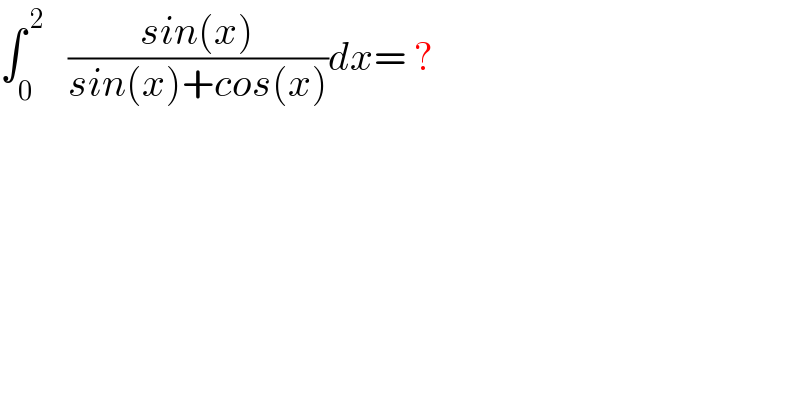
$$\int_{\mathrm{0}} ^{\:\mathrm{2}} \:\:\:\frac{{sin}\left({x}\right)}{{sin}\left({x}\right)+{cos}\left({x}\right)}{dx}=\:? \\ $$
Answered by ARUNG_Brandon_MBU last updated on 23/Mar/23
![I=∫_0 ^2 ((sinx)/(sinx+cosx))dx=(1/( (√2)))∫_0 ^2 ((sin((x−(π/4))+(π/4)))/(cos(x−(π/4))))dx =(1/( (√2)))∫_0 ^2 ((sin(x−(π/4))cos(π/4)+cos(x−(π/4))sin(π/4))/(cos(x−(π/4))))dx =(1/( 2))[lncos(x−(π/4))]_2 ^0 +[(x/( 2))]_0 ^2 =(1/( 2))ln((1/( (√2))))−(1/( 2))ln(((cos2+sin2)/( (√2))))+1 =1−(1/( 2))ln(cos(2)+sin(2))](https://www.tinkutara.com/question/Q189877.png)
$${I}=\int_{\mathrm{0}} ^{\mathrm{2}} \frac{\mathrm{sin}{x}}{\mathrm{sin}{x}+\mathrm{cos}{x}}{dx}=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\int_{\mathrm{0}} ^{\mathrm{2}} \frac{\mathrm{sin}\left(\left({x}−\frac{\pi}{\mathrm{4}}\right)+\frac{\pi}{\mathrm{4}}\right)}{\mathrm{cos}\left({x}−\frac{\pi}{\mathrm{4}}\right)}{dx} \\ $$$$\:\:\:=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\int_{\mathrm{0}} ^{\mathrm{2}} \frac{\mathrm{sin}\left({x}−\frac{\pi}{\mathrm{4}}\right)\mathrm{cos}\frac{\pi}{\mathrm{4}}+\mathrm{cos}\left({x}−\frac{\pi}{\mathrm{4}}\right)\mathrm{sin}\frac{\pi}{\mathrm{4}}}{\mathrm{cos}\left({x}−\frac{\pi}{\mathrm{4}}\right)}{dx} \\ $$$$\:\:\:=\frac{\mathrm{1}}{\:\mathrm{2}}\left[\mathrm{lncos}\left({x}−\frac{\pi}{\mathrm{4}}\right)\right]_{\mathrm{2}} ^{\mathrm{0}} +\left[\frac{{x}}{\:\mathrm{2}}\right]_{\mathrm{0}} ^{\mathrm{2}} \\ $$$$\:\:\:=\frac{\mathrm{1}}{\:\mathrm{2}}\mathrm{ln}\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\right)−\frac{\mathrm{1}}{\:\mathrm{2}}\mathrm{ln}\left(\frac{\mathrm{cos2}+\mathrm{sin2}}{\:\sqrt{\mathrm{2}}}\right)+\mathrm{1} \\ $$$$\:\:\:=\mathrm{1}−\frac{\mathrm{1}}{\:\mathrm{2}}\mathrm{ln}\left(\mathrm{cos}\left(\mathrm{2}\right)+\mathrm{sin}\left(\mathrm{2}\right)\right) \\ $$
Commented by mathocean1 last updated on 26/Mar/23

$${Thanks}… \\ $$
Answered by mehdee42 last updated on 23/Mar/23
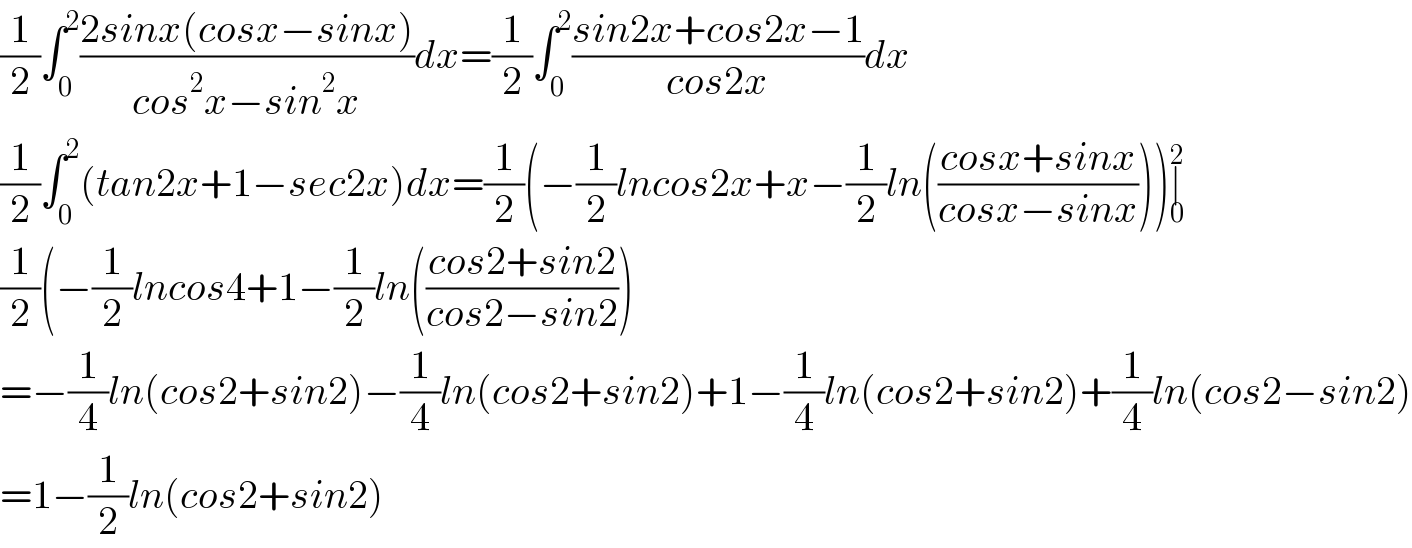
$$\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{2}} \frac{\mathrm{2}{sinx}\left({cosx}−{sinx}\right)}{{cos}^{\mathrm{2}} {x}−{sin}^{\mathrm{2}} {x}}{dx}=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{2}} \frac{{sin}\mathrm{2}{x}+{cos}\mathrm{2}{x}−\mathrm{1}}{{cos}\mathrm{2}{x}}{dx} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{2}} \left({tan}\mathrm{2}{x}+\mathrm{1}−{sec}\mathrm{2}{x}\right){dx}=\frac{\mathrm{1}}{\mathrm{2}}\left(−\frac{\mathrm{1}}{\mathrm{2}}{lncos}\mathrm{2}{x}+{x}−\frac{\mathrm{1}}{\mathrm{2}}{ln}\left(\frac{{cosx}+{sinx}}{{cosx}−{sinx}}\right)\right)\underset{\mathrm{0}} {\overset{\mathrm{2}} {\mid}} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\left(−\frac{\mathrm{1}}{\mathrm{2}}{lncos}\mathrm{4}+\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}{ln}\left(\frac{{cos}\mathrm{2}+{sin}\mathrm{2}}{{cos}\mathrm{2}−{sin}\mathrm{2}}\right)\right. \\ $$$$=−\frac{\mathrm{1}}{\mathrm{4}}{ln}\left({cos}\mathrm{2}+{sin}\mathrm{2}\right)−\frac{\mathrm{1}}{\mathrm{4}}{ln}\left({cos}\mathrm{2}+{sin}\mathrm{2}\right)+\mathrm{1}−\frac{\mathrm{1}}{\mathrm{4}}{ln}\left({cos}\mathrm{2}+{sin}\mathrm{2}\right)+\frac{\mathrm{1}}{\mathrm{4}}{ln}\left({cos}\mathrm{2}−{sin}\mathrm{2}\right) \\ $$$$=\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}{ln}\left({cos}\mathrm{2}+{sin}\mathrm{2}\right) \\ $$
Commented by mathocean1 last updated on 26/Mar/23

$${Thanks}… \\ $$
