Question Number 84055 by naka3546 last updated on 09/Mar/20
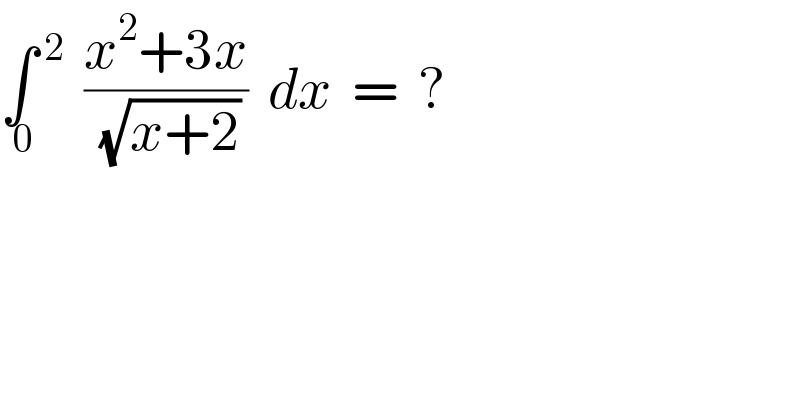
$$\underset{\:\mathrm{0}} {\int}\overset{\:\mathrm{2}} {\:}\:\:\frac{{x}^{\mathrm{2}} +\mathrm{3}{x}}{\:\sqrt{{x}+\mathrm{2}}}\:\:{dx}\:\:=\:\:? \\ $$
Commented by mathmax by abdo last updated on 09/Mar/20
![A =∫_0 ^2 ((x^2 +3x)/( (√(x+2))))dx we do the changement (√(x+2))=t ⇒x+2=t^2 A =∫_(√2) ^2 (((t^2 −2)^2 +3(t^2 −2))/t)(2t)dt =2 ∫_(√2) ^2 { t^4 −4t^2 +4 +3t^2 −6)dt =2[(t^5 /5)−(4/3)t^3 +t^3 −2t]_(√2) ^2 =2{ ((32)/5)−((32)/3) +4 −((((√2))^5 )/5)+(4/3)((√2))^3 −2(√2)+2(√2)}=...](https://www.tinkutara.com/question/Q84148.png)
$${A}\:=\int_{\mathrm{0}} ^{\mathrm{2}} \:\frac{{x}^{\mathrm{2}} \:+\mathrm{3}{x}}{\:\sqrt{{x}+\mathrm{2}}}{dx}\:{we}\:{do}\:{the}\:{changement}\:\sqrt{{x}+\mathrm{2}}={t}\:\Rightarrow{x}+\mathrm{2}={t}^{\mathrm{2}} \\ $$$${A}\:=\int_{\sqrt{\mathrm{2}}} ^{\mathrm{2}} \:\:\:\frac{\left({t}^{\mathrm{2}} −\mathrm{2}\right)^{\mathrm{2}} +\mathrm{3}\left({t}^{\mathrm{2}} −\mathrm{2}\right)}{{t}}\left(\mathrm{2}{t}\right){dt} \\ $$$$=\mathrm{2}\:\int_{\sqrt{\mathrm{2}}} ^{\mathrm{2}} \:\left\{\:{t}^{\mathrm{4}} −\mathrm{4}{t}^{\mathrm{2}} \:+\mathrm{4}\:+\mathrm{3}{t}^{\mathrm{2}} −\mathrm{6}\right){dt} \\ $$$$=\mathrm{2}\left[\frac{{t}^{\mathrm{5}} }{\mathrm{5}}−\frac{\mathrm{4}}{\mathrm{3}}{t}^{\mathrm{3}} \:+{t}^{\mathrm{3}} \:−\mathrm{2}{t}\right]_{\sqrt{\mathrm{2}}} ^{\mathrm{2}} \\ $$$$=\mathrm{2}\left\{\:\frac{\mathrm{32}}{\mathrm{5}}−\frac{\mathrm{32}}{\mathrm{3}}\:+\mathrm{4}\:\:−\frac{\left(\sqrt{\mathrm{2}}\right)^{\mathrm{5}} }{\mathrm{5}}+\frac{\mathrm{4}}{\mathrm{3}}\left(\sqrt{\mathrm{2}}\right)^{\mathrm{3}} −\mathrm{2}\sqrt{\mathrm{2}}+\mathrm{2}\sqrt{\mathrm{2}}\right\}=… \\ $$
Answered by john santu last updated on 09/Mar/20
![let (√(x+2)) =t ⇒ x = t^2 −2 ∫ _( (√2)) ^( 2) (((t^2 −2)(t^2 +1)2t dt)/t) = 2∫ _( (√2) ) ^( 2) (t^4 −t^2 −2)dt = 2 [ (1/5)t^5 −(1/3)t^3 −2t ]_(√2) ^2 = 2 [(1/5)(32−4(√2))−(1/3)(8−2(√2))−2(2−(√2)) ]](https://www.tinkutara.com/question/Q84056.png)
$$\mathrm{let}\:\sqrt{\mathrm{x}+\mathrm{2}}\:=\mathrm{t}\:\Rightarrow\:\mathrm{x}\:=\:\mathrm{t}^{\mathrm{2}} −\mathrm{2} \\ $$$$\int\underset{\:\sqrt{\mathrm{2}}} {\overset{\:\mathrm{2}} {\:}}\:\frac{\left(\mathrm{t}^{\mathrm{2}} −\mathrm{2}\right)\left(\mathrm{t}^{\mathrm{2}} +\mathrm{1}\right)\mathrm{2t}\:\mathrm{dt}}{\mathrm{t}} \\ $$$$=\:\mathrm{2}\int\underset{\:\sqrt{\mathrm{2}}\:} {\overset{\:\mathrm{2}} {\:}}\left(\mathrm{t}^{\mathrm{4}} −\mathrm{t}^{\mathrm{2}} −\mathrm{2}\right)\mathrm{dt} \\ $$$$=\:\mathrm{2}\:\left[\:\frac{\mathrm{1}}{\mathrm{5}}\mathrm{t}^{\mathrm{5}} −\frac{\mathrm{1}}{\mathrm{3}}\mathrm{t}^{\mathrm{3}} −\mathrm{2t}\:\right]_{\sqrt{\mathrm{2}}} ^{\mathrm{2}} \\ $$$$=\:\mathrm{2}\:\left[\frac{\mathrm{1}}{\mathrm{5}}\left(\mathrm{32}−\mathrm{4}\sqrt{\mathrm{2}}\right)−\frac{\mathrm{1}}{\mathrm{3}}\left(\mathrm{8}−\mathrm{2}\sqrt{\mathrm{2}}\right)−\mathrm{2}\left(\mathrm{2}−\sqrt{\mathrm{2}}\right)\:\right] \\ $$
