Question Number 151614 by mathdanisur last updated on 22/Aug/21
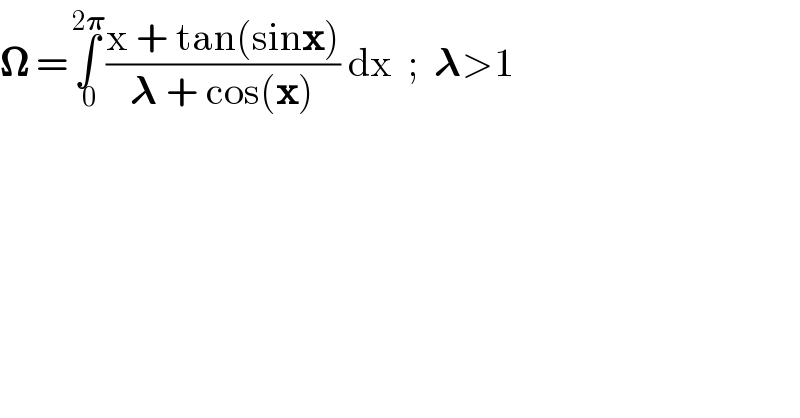
$$\boldsymbol{\Omega}\:=\underset{\:\mathrm{0}} {\overset{\:\mathrm{2}\boldsymbol{\pi}} {\int}}\frac{\mathrm{x}\:+\:\mathrm{tan}\left(\mathrm{sin}\boldsymbol{\mathrm{x}}\right)}{\boldsymbol{\lambda}\:+\:\mathrm{cos}\left(\boldsymbol{\mathrm{x}}\right)}\:\mathrm{dx}\:\:;\:\:\boldsymbol{\lambda}>\mathrm{1} \\ $$
Answered by ArielVyny last updated on 22/Aug/21
![Ω=∫_0 ^(2π) ((x+tan(sinx))/(λ+cos(x)))dx x=2π−t ∫_0 ^(2π) (((2π−t)−tan(sint))/(λ+cos(t)))dt=∫_0 ^(2π) ((x+tan(sin(x)))/(λ+cos(x)))dx 2π∫_0 ^(2π) (1/(λ+cos(t)))dt=2Ω→Ω=π∫_0 ^(2π) (1/(λ+cos(x)))dx Ω=2π∫_0 ^π (1/(λ+cos(x)))dx u=tan((x/2))→du=(1/2)(1+u^2 )dx Ω=2π∫_0 ^∞ (1/(λ+((1−u^2 )/(1+u^2 ))))×(2/(1+u^2 ))du=4π∫_0 ^∞ (1/(λ(1+u^2 )+(1−u^2 )))du Ω=4π∫_0 ^∞ (1/(u^2 (λ−1)+λ+1))du Ω=4π∫_0 ^∞ (1/((λ−1)[u^2 +((λ+1)/(λ−1))]))du=((4π)/(λ−1))∫_0 ^∞ (1/(u^2 +(((λ+1)/(λ−1)))))du Ω=((4π)/(λ−1))∫_0 ^∞ (1/((((λ+1)/(λ−1)))[1+(u^2 /((λ+1)/(λ−1)))]))du Ω=((4π)/(λ+1))∫_0 ^∞ (1/(1+[u(√((λ−1)/(λ+1)))]^2 ))du γ=u(√((λ−1)/(λ+1)))→dγ=(√((λ−1)/(λ+1)))du Ω=((4π)/(λ+1))∫_0 ^∞ (1/(1+γ^2 ))(√((λ+1)/(λ−1)))dγ=((4π)/( (√(λ^2 −1))))[(π/2)] Ω=((2π^2 )/( (√(λ^2 −1))))](https://www.tinkutara.com/question/Q151755.png)
$$\Omega=\int_{\mathrm{0}} ^{\mathrm{2}\pi} \frac{{x}+{tan}\left({sinx}\right)}{\lambda+{cos}\left({x}\right)}{dx} \\ $$$${x}=\mathrm{2}\pi−{t} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{2}\pi} \frac{\left(\mathrm{2}\pi−{t}\right)−{tan}\left({sint}\right)}{\lambda+{cos}\left({t}\right)}{dt}=\int_{\mathrm{0}} ^{\mathrm{2}\pi} \frac{{x}+{tan}\left({sin}\left({x}\right)\right)}{\lambda+{cos}\left({x}\right)}{dx} \\ $$$$\mathrm{2}\pi\int_{\mathrm{0}} ^{\mathrm{2}\pi} \frac{\mathrm{1}}{\lambda+{cos}\left({t}\right)}{dt}=\mathrm{2}\Omega\rightarrow\Omega=\pi\int_{\mathrm{0}} ^{\mathrm{2}\pi} \frac{\mathrm{1}}{\lambda+{cos}\left({x}\right)}{dx} \\ $$$$\Omega=\mathrm{2}\pi\int_{\mathrm{0}} ^{\pi} \frac{\mathrm{1}}{\lambda+{cos}\left({x}\right)}{dx} \\ $$$${u}={tan}\left(\frac{{x}}{\mathrm{2}}\right)\rightarrow{du}=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}+{u}^{\mathrm{2}} \right){dx} \\ $$$$\Omega=\mathrm{2}\pi\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{1}}{\lambda+\frac{\mathrm{1}−{u}^{\mathrm{2}} }{\mathrm{1}+{u}^{\mathrm{2}} }}×\frac{\mathrm{2}}{\mathrm{1}+{u}^{\mathrm{2}} }{du}=\mathrm{4}\pi\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{1}}{\lambda\left(\mathrm{1}+{u}^{\mathrm{2}} \right)+\left(\mathrm{1}−{u}^{\mathrm{2}} \right)}{du} \\ $$$$\Omega=\mathrm{4}\pi\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{1}}{{u}^{\mathrm{2}} \left(\lambda−\mathrm{1}\right)+\lambda+\mathrm{1}}{du} \\ $$$$\Omega=\mathrm{4}\pi\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{1}}{\left(\lambda−\mathrm{1}\right)\left[{u}^{\mathrm{2}} +\frac{\lambda+\mathrm{1}}{\lambda−\mathrm{1}}\right]}{du}=\frac{\mathrm{4}\pi}{\lambda−\mathrm{1}}\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{1}}{{u}^{\mathrm{2}} +\left(\frac{\lambda+\mathrm{1}}{\lambda−\mathrm{1}}\right)}{du} \\ $$$$\Omega=\frac{\mathrm{4}\pi}{\lambda−\mathrm{1}}\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{1}}{\left(\frac{\lambda+\mathrm{1}}{\lambda−\mathrm{1}}\right)\left[\mathrm{1}+\frac{{u}^{\mathrm{2}} }{\frac{\lambda+\mathrm{1}}{\lambda−\mathrm{1}}}\right]}{du} \\ $$$$\Omega=\frac{\mathrm{4}\pi}{\lambda+\mathrm{1}}\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{1}}{\mathrm{1}+\left[{u}\sqrt{\frac{\lambda−\mathrm{1}}{\lambda+\mathrm{1}}}\right]^{\mathrm{2}} }{du} \\ $$$$\gamma={u}\sqrt{\frac{\lambda−\mathrm{1}}{\lambda+\mathrm{1}}}\rightarrow{d}\gamma=\sqrt{\frac{\lambda−\mathrm{1}}{\lambda+\mathrm{1}}}{du} \\ $$$$\Omega=\frac{\mathrm{4}\pi}{\lambda+\mathrm{1}}\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{1}}{\mathrm{1}+\gamma^{\mathrm{2}} }\sqrt{\frac{\lambda+\mathrm{1}}{\lambda−\mathrm{1}}}{d}\gamma=\frac{\mathrm{4}\pi}{\:\sqrt{\lambda^{\mathrm{2}} −\mathrm{1}}}\left[\frac{\pi}{\mathrm{2}}\right] \\ $$$$\Omega=\frac{\mathrm{2}\pi^{\mathrm{2}} }{\:\sqrt{\lambda^{\mathrm{2}} −\mathrm{1}}} \\ $$$$ \\ $$$$ \\ $$
Commented by ArielVyny last updated on 22/Aug/21

$$\lambda>\mathrm{1} \\ $$
