Question Number 17219 by Arnab Maiti last updated on 02/Jul/17
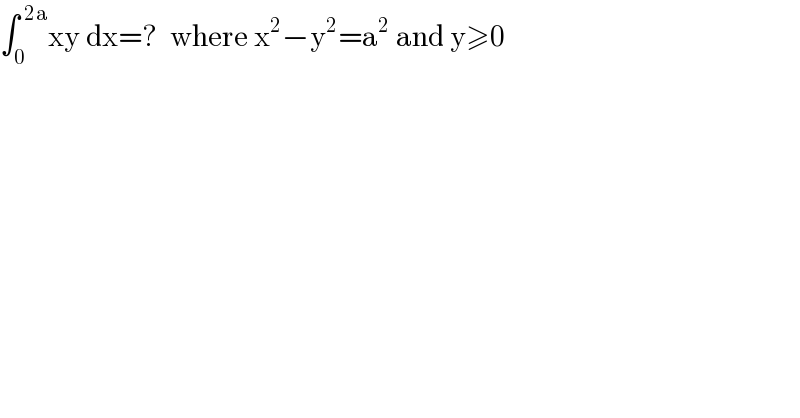
$$\int_{\mathrm{0}} ^{\:\mathrm{2a}} \mathrm{xy}\:\mathrm{dx}=?\:\:\mathrm{where}\:\mathrm{x}^{\mathrm{2}} −\mathrm{y}^{\mathrm{2}} =\mathrm{a}^{\mathrm{2}} \:\mathrm{and}\:\mathrm{y}\geqslant\mathrm{0} \\ $$
Commented by Arnab Maiti last updated on 02/Jul/17
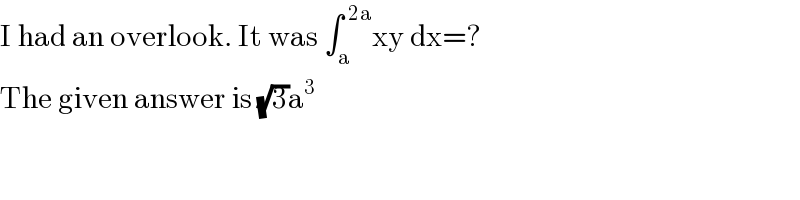
$$\mathrm{I}\:\mathrm{had}\:\mathrm{an}\:\mathrm{overlook}.\:\mathrm{It}\:\mathrm{was}\:\int_{\mathrm{a}} ^{\:\mathrm{2a}} \mathrm{xy}\:\mathrm{dx}=? \\ $$$$\mathrm{The}\:\mathrm{given}\:\mathrm{answer}\:\mathrm{is}\:\sqrt{\mathrm{3}}\mathrm{a}^{\mathrm{3}} \\ $$
Answered by ajfour last updated on 02/Jul/17
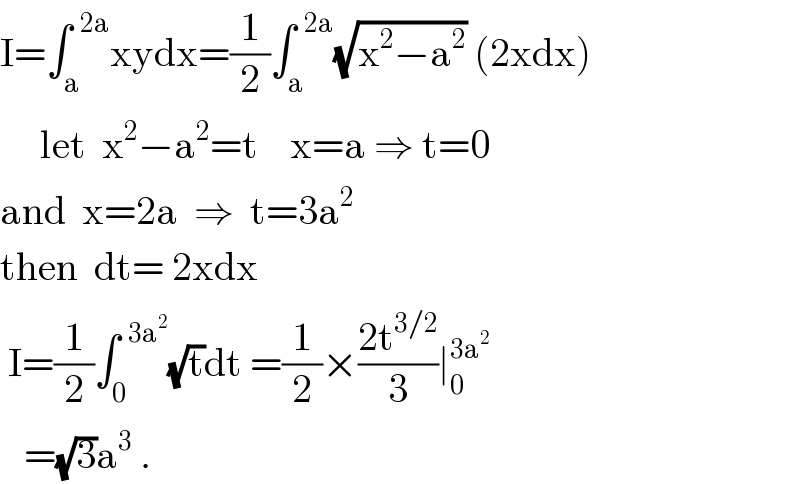
$$\mathrm{I}=\int_{\mathrm{a}} ^{\:\:\mathrm{2a}} \mathrm{xydx}=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{a}} ^{\:\:\mathrm{2a}} \sqrt{\mathrm{x}^{\mathrm{2}} −\mathrm{a}^{\mathrm{2}} }\:\left(\mathrm{2xdx}\right) \\ $$$$\:\:\:\:\:\mathrm{let}\:\:\mathrm{x}^{\mathrm{2}} −\mathrm{a}^{\mathrm{2}} =\mathrm{t}\:\:\:\:\mathrm{x}=\mathrm{a}\:\Rightarrow\:\mathrm{t}=\mathrm{0} \\ $$$$\mathrm{and}\:\:\mathrm{x}=\mathrm{2a}\:\:\Rightarrow\:\:\mathrm{t}=\mathrm{3a}^{\mathrm{2}} \\ $$$$\mathrm{then}\:\:\mathrm{dt}=\:\mathrm{2xdx} \\ $$$$\:\mathrm{I}=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\:\:\mathrm{3a}^{\mathrm{2}} } \sqrt{\mathrm{t}}\mathrm{dt}\:=\frac{\mathrm{1}}{\mathrm{2}}×\frac{\mathrm{2t}^{\mathrm{3}/\mathrm{2}} }{\mathrm{3}}\mid_{\mathrm{0}} ^{\mathrm{3a}^{\mathrm{2}} } \\ $$$$\:\:\:=\sqrt{\mathrm{3}}\mathrm{a}^{\mathrm{3}} \:. \\ $$
Commented by Arnab Maiti last updated on 02/Jul/17

$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{sir}. \\ $$
