Question Number 43145 by rahul 19 last updated on 07/Sep/18
![∫_0 ^∞ [ 2e^(−x) ]dx = ? where [.]= gif.](https://www.tinkutara.com/question/Q43145.png)
$$\int_{\mathrm{0}} ^{\infty} \:\left[\:\mathrm{2e}^{−{x}} \right]{dx}\:=\:?\: \\ $$$${where}\:\left[.\right]=\:{gif}. \\ $$
Commented by maxmathsup by imad last updated on 07/Sep/18
![changement 2 e^(−x) =t give e^(−x) =(t/2) ⇒−x=ln((t/2)) ⇒x=−ln((t/2)) and I = ∫_0 ^∞ [ 2 e^(−x) ]dx =−∫_0 ^2 [t](−(1/t))dt = ∫_0 ^2 (([t])/t)dt = ∫_0 ^1 (0/t)dt +∫_1 ^2 (1/t)dt = [ln∣t∣]_1 ^2 =ln(2) .](https://www.tinkutara.com/question/Q43154.png)
$${changement}\:\mathrm{2}\:{e}^{−{x}} \:={t}\:{give}\:{e}^{−{x}} =\frac{{t}}{\mathrm{2}}\:\Rightarrow−{x}={ln}\left(\frac{{t}}{\mathrm{2}}\right)\:\Rightarrow{x}=−{ln}\left(\frac{{t}}{\mathrm{2}}\right)\:{and} \\ $$$${I}\:=\:\int_{\mathrm{0}} ^{\infty} \:\:\left[\:\mathrm{2}\:{e}^{−{x}} \right]{dx}\:=−\int_{\mathrm{0}} ^{\mathrm{2}} \:\left[{t}\right]\left(−\frac{\mathrm{1}}{{t}}\right){dt}\:=\:\int_{\mathrm{0}} ^{\mathrm{2}} \:\:\frac{\left[{t}\right]}{{t}}{dt} \\ $$$$=\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{0}}{{t}}{dt}\:+\int_{\mathrm{1}} ^{\mathrm{2}} \:\frac{\mathrm{1}}{{t}}{dt}\:=\:\left[{ln}\mid{t}\mid\right]_{\mathrm{1}} ^{\mathrm{2}} \:\:={ln}\left(\mathrm{2}\right)\:. \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 07/Sep/18

Commented by rahul 19 last updated on 08/Sep/18

$$\mathrm{thanks}\:\mathrm{prof}\:\mathrm{abdo}. \\ $$
Commented by math khazana by abdo last updated on 08/Sep/18
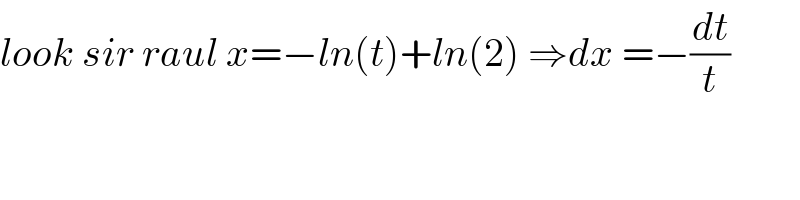
$${look}\:{sir}\:{raul}\:{x}=−{ln}\left({t}\right)+{ln}\left(\mathrm{2}\right)\:\Rightarrow{dx}\:=−\frac{{dt}}{{t}} \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 07/Sep/18
![∫_0 ^(0.7) [2e^(−x) ]dx+∫_(0.7) ^∞ [2e^(−x) ]dx =∫_0 ^(0.7) 1×dx+∫_(0.7) ^∞ 0×dx =0.7 ln2≈0.7](https://www.tinkutara.com/question/Q43167.png)
$$\int_{\mathrm{0}} ^{\mathrm{0}.\mathrm{7}} \left[\mathrm{2}{e}^{−{x}} \right]{dx}+\int_{\mathrm{0}.\mathrm{7}} ^{\infty} \left[\mathrm{2}{e}^{−{x}} \right]{dx} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{0}.\mathrm{7}} \mathrm{1}×{dx}+\int_{\mathrm{0}.\mathrm{7}} ^{\infty} \mathrm{0}×{dx} \\ $$$$=\mathrm{0}.\mathrm{7} \\ $$$${ln}\mathrm{2}\approx\mathrm{0}.\mathrm{7} \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 07/Sep/18

Commented by rahul 19 last updated on 08/Sep/18

$$\mathrm{thanks}\:\mathrm{sir}. \\ $$
Commented by abdo.msup.com last updated on 08/Sep/18

$${nevermind}\:{sir}… \\ $$
