Menu Close

0-2pi-1-a-2-cos-2-t-b-2-sin-2-t-dt-2pi-ab-

Tinku Tara 0 Comments
Pin




Question Number 61465 by arcana last updated on 02/Jun/19
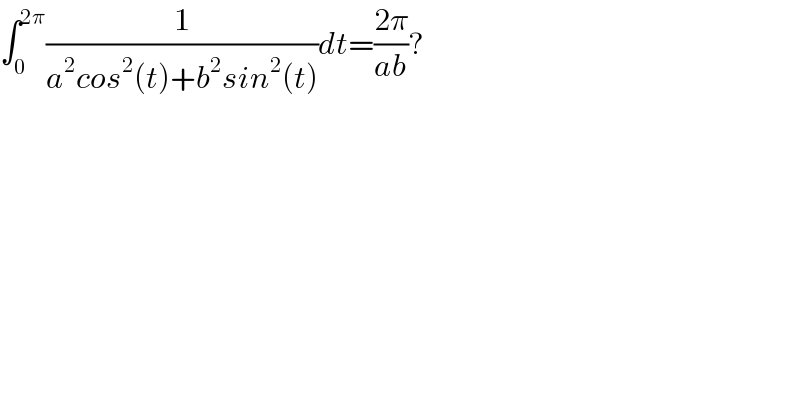
∫_0 ^(2π) (1/(a^2 cos^2 (t)+b^2 sin^2 (t)))dt=((2π)/(ab))?
$$\int_{\mathrm{0}} ^{\mathrm{2}\pi} \frac{\mathrm{1}}{{a}^{\mathrm{2}} {cos}^{\mathrm{2}} \left({t}\right)+{b}^{\mathrm{2}} {sin}^{\mathrm{2}} \left({t}\right)}{dt}=\frac{\mathrm{2}\pi}{{ab}}? \\ $$
Commented by maxmathsup by imad last updated on 03/Jun/19
let A =∫_0 ^(2π) (dt/(a^2 cos^2 t +b^2 sin^2 t)) ⇒A =∫_0 ^(2π) ((2dt)/(a^2 (1+cos(2t))+b^2 (1−cos(2t))) =∫_0 ^(2π) ((2dt)/(a^2 +b^2 +(a^2 −b^2 )cos(2t))) =_(2t =x) ∫_0 ^(4π) (dx/(a^2 +b^2 +(a^2 −b^2 )cos(x))) =∫_0 ^(2π) (dx/(a^2 +b^2 +(a^2 −b^2 )cos(x))) +∫_(2π) ^(4π) (dx/(a^2 +b^2 +(a^2 −b^2 )cos(x))) =H+K H =_(e^(ix) =z) ∫_(∣z∣=1) (dz/(iz{ a^2 +b^2 +(a^2 −b^2 )((z+z^(−1) )/2)})) =∫_(∣z∣=1) ((2dz)/(iz{2(a^2 +b^2 )+(a^2 −b^2 )(z+z^(−1) )})) = ∫_(∣z∣=1) ((2dz)/(2i(a^2 +b^2 )z +i(a^2 −b^2 )z^2 +i(a^2 −b^2 ))) =∫ ((−2i dz)/((a^2 −b^2 )z^2 +2(a^2 +b^2 )z +a^2 −b^2 )) let ϕ(z) =((−2i)/((a^2 −b^2 )z^2 +2(a^2 +b^2 )z +a^2 −b^2 )) Δ_d ^′ = =(a^2 +b^2 )^2 −(a^2 −b^2 )^2 =a^4 +2a^2 b^2 +b^4 −a^4 +2a^2 b^2 −b^4 =4a^2 b^2 ⇒ z_1 =((−a^2 −b^2 +2∣ab∣)/(a^2 −b^2 )) =−(((∣a∣−∣b∣)^2 )/(∣a∣^2 −∣b∣^2 )) =−((∣a∣−∣b∣)/(∣a∣+∣b∣)) (a≠b) z_2 =((−a^2 −b^2 −2∣ab∣)/(a^2 −b^2 )) =−(((∣a∣+∣b∣)^2 )/(a^2 −b^2 )) =−((∣a∣+∣b∣)/(∣a∣−∣b∣)) (=(1/z_1 ))∣z ∣z_1 ∣−1 =((∣∣a∣−∣b∣∣)/(∣a∣+∣b∣)) −1 = ((∣∣a∣−∣b∣∣−(∣a∣+∣b∣))/((....)))<0 ∣z_2 ∣−1 >0 (to eliminate from residus ⇒ ∫_(∣z∣=1) ϕ(z)dz =2iπ Res(ϕ ,z_1 ) we have ϕ(z) = ((−2i)/((a^2 −b^2 )(z−z_1 )(z−z_2 ))) ⇎ Res(ϕ,z_1 ) =((−2i)/((a^2 −b^2 )(z_1 −z_2 ))) =((−2i)/((a^2 −b^2 )(((∣a∣+∣b∣)/(∣a∣−∣b∣))−((∣a∣−∣b∣)/(∣a∣+∣b∣))))) =((−2i)/((∣a∣+∣b∣)^2 −(∣a∣−∣b∣)^2 )) =((−2i)/(4∣ab∣)) =−(i/(2∣ab∣)) ⇒∫_(∣z∣=1) ϕ(z)dz =2iπ ((−i)/(2∣ab∣)) = (π/(∣ab∣)) =H K =_(x=2π +t) ∫_0 ^(2π) (dt/(a^2 +b^2 +(a^2 −b^2 )cost)) =H ⇒ ∫_0 ^(2π) (dt/(a^2 cos^2 t +b^2 sin^2 t)) =2H = ((2π)/(∣ab∣)) if a=b we get ∫_0 ^(2π) (dt/(a^2 cos^2 t +b^2 sin^2 t)) = (1/a^2 ) (2π) =((2π)/a^2 ) .
$${let}\:{A}\:=\int_{\mathrm{0}} ^{\mathrm{2}\pi} \:\:\frac{{dt}}{{a}^{\mathrm{2}} {cos}^{\mathrm{2}} {t}\:+{b}^{\mathrm{2}} {sin}^{\mathrm{2}} {t}}\:\Rightarrow{A}\:=\int_{\mathrm{0}} ^{\mathrm{2}\pi} \:\:\:\frac{\mathrm{2}{dt}}{{a}^{\mathrm{2}} \left(\mathrm{1}+{cos}\left(\mathrm{2}{t}\right)\right)+{b}^{\mathrm{2}} \left(\mathrm{1}−{cos}\left(\mathrm{2}{t}\right)\right.} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{2}\pi} \:\:\frac{\mathrm{2}{dt}}{{a}^{\mathrm{2}} \:+{b}^{\mathrm{2}} \:+\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right){cos}\left(\mathrm{2}{t}\right)}\:=_{\mathrm{2}{t}\:={x}} \:\:\:\:\:\int_{\mathrm{0}} ^{\mathrm{4}\pi} \:\:\:\frac{{dx}}{{a}^{\mathrm{2}} \:+{b}^{\mathrm{2}} \:+\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right){cos}\left({x}\right)} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{2}\pi} \:\frac{{dx}}{{a}^{\mathrm{2}} \:+{b}^{\mathrm{2}} \:\:+\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right){cos}\left({x}\right)}\:+\int_{\mathrm{2}\pi} ^{\mathrm{4}\pi} \:\:\:\frac{{dx}}{{a}^{\mathrm{2}} \:+{b}^{\mathrm{2}} \:+\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right){cos}\left({x}\right)}\:={H}+{K} \\ $$$${H}\:=_{{e}^{{ix}} ={z}} \:\:\:\:\int_{\mid{z}\mid=\mathrm{1}} \:\:\:\:\frac{{dz}}{{iz}\left\{\:{a}^{\mathrm{2}} \:+{b}^{\mathrm{2}} \:+\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)\frac{{z}+{z}^{−\mathrm{1}} }{\mathrm{2}}\right\}}\:=\int_{\mid{z}\mid=\mathrm{1}} \:\:\frac{\mathrm{2}{dz}}{{iz}\left\{\mathrm{2}\left({a}^{\mathrm{2}} \:+{b}^{\mathrm{2}} \right)+\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)\left({z}+{z}^{−\mathrm{1}} \right)\right\}} \\ $$$$=\:\int_{\mid{z}\mid=\mathrm{1}} \:\:\:\:\:\frac{\mathrm{2}{dz}}{\mathrm{2}{i}\left({a}^{\mathrm{2}} \:+{b}^{\mathrm{2}} \right){z}\:+{i}\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right){z}^{\mathrm{2}} \:+{i}\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)} \\ $$$$=\int\:\:\frac{−\mathrm{2}{i}\:{dz}}{\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right){z}^{\mathrm{2}} +\mathrm{2}\left({a}^{\mathrm{2}} \:+{b}^{\mathrm{2}} \right){z}\:+{a}^{\mathrm{2}} −{b}^{\mathrm{2}} }\:{let}\:\varphi\left({z}\right)\:=\frac{−\mathrm{2}{i}}{\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right){z}^{\mathrm{2}} \:+\mathrm{2}\left({a}^{\mathrm{2}} \:+{b}^{\mathrm{2}} \right){z}\:+{a}^{\mathrm{2}} −{b}^{\mathrm{2}} } \\ $$$$\Delta_{{d}} ^{'} =\:\:=\left({a}^{\mathrm{2}} \:+{b}^{\mathrm{2}} \right)^{\mathrm{2}} −\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)^{\mathrm{2}} \:={a}^{\mathrm{4}} \:+\mathrm{2}{a}^{\mathrm{2}} {b}^{\mathrm{2}} \:+{b}^{\mathrm{4}} −{a}^{\mathrm{4}} +\mathrm{2}{a}^{\mathrm{2}} {b}^{\mathrm{2}} −{b}^{\mathrm{4}} \:=\mathrm{4}{a}^{\mathrm{2}} {b}^{\mathrm{2}} \:\:\Rightarrow \\ $$$${z}_{\mathrm{1}} =\frac{−{a}^{\mathrm{2}} −{b}^{\mathrm{2}} +\mathrm{2}\mid{ab}\mid}{{a}^{\mathrm{2}} −{b}^{\mathrm{2}} }\:\:=−\frac{\left(\mid{a}\mid−\mid{b}\mid\right)^{\mathrm{2}} }{\mid{a}\mid^{\mathrm{2}} −\mid{b}\mid^{\mathrm{2}} }\:=−\frac{\mid{a}\mid−\mid{b}\mid}{\mid{a}\mid+\mid{b}\mid}\:\:\:\:\:\left({a}\neq{b}\right) \\ $$$${z}_{\mathrm{2}} =\frac{−{a}^{\mathrm{2}} −{b}^{\mathrm{2}} −\mathrm{2}\mid{ab}\mid}{{a}^{\mathrm{2}} −{b}^{\mathrm{2}} }\:=−\frac{\left(\mid{a}\mid+\mid{b}\mid\right)^{\mathrm{2}} }{{a}^{\mathrm{2}} −{b}^{\mathrm{2}} }\:=−\frac{\mid{a}\mid+\mid{b}\mid}{\mid{a}\mid−\mid{b}\mid}\:\left(=\frac{\mathrm{1}}{{z}_{\mathrm{1}} }\right)\mid{z} \\ $$$$\mid{z}_{\mathrm{1}} \mid−\mathrm{1}\:=\frac{\mid\mid{a}\mid−\mid{b}\mid\mid}{\mid{a}\mid+\mid{b}\mid}\:−\mathrm{1}\:=\:\frac{\mid\mid{a}\mid−\mid{b}\mid\mid−\left(\mid{a}\mid+\mid{b}\mid\right)}{\left(….\right)}<\mathrm{0} \\ $$$$\mid{z}_{\mathrm{2}} \mid−\mathrm{1}\:>\mathrm{0}\:\:\left({to}\:{eliminate}\:{from}\:{residus}\:\Rightarrow\right. \\ $$$$\int_{\mid{z}\mid=\mathrm{1}} \:\varphi\left({z}\right){dz}\:=\mathrm{2}{i}\pi\:{Res}\left(\varphi\:,{z}_{\mathrm{1}} \right)\:{we}\:{have}\:\varphi\left({z}\right)\:=\:\frac{−\mathrm{2}{i}}{\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)\left({z}−{z}_{\mathrm{1}} \right)\left({z}−{z}_{\mathrm{2}} \right)}\:\nLeftrightarrow \\ $$$${Res}\left(\varphi,{z}_{\mathrm{1}} \right)\:=\frac{−\mathrm{2}{i}}{\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)\left({z}_{\mathrm{1}} −{z}_{\mathrm{2}} \right)}\:=\frac{−\mathrm{2}{i}}{\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)\left(\frac{\mid{a}\mid+\mid{b}\mid}{\mid{a}\mid−\mid{b}\mid}−\frac{\mid{a}\mid−\mid{b}\mid}{\mid{a}\mid+\mid{b}\mid}\right)}\:=\frac{−\mathrm{2}{i}}{\left(\mid{a}\mid+\mid{b}\mid\right)^{\mathrm{2}} −\left(\mid{a}\mid−\mid{b}\mid\right)^{\mathrm{2}} } \\ $$$$=\frac{−\mathrm{2}{i}}{\mathrm{4}\mid{ab}\mid}\:=−\frac{{i}}{\mathrm{2}\mid{ab}\mid}\:\Rightarrow\int_{\mid{z}\mid=\mathrm{1}} \:\varphi\left({z}\right){dz}\:=\mathrm{2}{i}\pi\:\frac{−{i}}{\mathrm{2}\mid{ab}\mid}\:=\:\frac{\pi}{\mid{ab}\mid}\:={H} \\ $$$${K}\:=_{{x}=\mathrm{2}\pi\:+{t}} \:\:\:\int_{\mathrm{0}} ^{\mathrm{2}\pi} \:\:\:\:\:\frac{{dt}}{{a}^{\mathrm{2}} \:+{b}^{\mathrm{2}} \:+\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right){cost}}\:={H}\:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\mathrm{2}\pi} \:\:\:\frac{{dt}}{{a}^{\mathrm{2}} {cos}^{\mathrm{2}} {t}\:+{b}^{\mathrm{2}} {sin}^{\mathrm{2}} {t}}\:=\mathrm{2}{H}\:\:=\:\frac{\mathrm{2}\pi}{\mid{ab}\mid} \\ $$$${if}\:{a}={b}\:{we}\:{get}\:\:\int_{\mathrm{0}} ^{\mathrm{2}\pi} \:\:\frac{{dt}}{{a}^{\mathrm{2}} {cos}^{\mathrm{2}} {t}\:+{b}^{\mathrm{2}} {sin}^{\mathrm{2}} {t}}\:=\:\frac{\mathrm{1}}{{a}^{\mathrm{2}} }\:\left(\mathrm{2}\pi\right)\:=\frac{\mathrm{2}\pi}{{a}^{\mathrm{2}} }\:. \\ $$
Answered by tanmay last updated on 03/Jun/19
∫_0 ^(2π) ((sec^2 t)/(a^2 +b^2 tan^2 t))dt (1/b^2 )∫_0 ^(2π) ((d(tant))/(((a/b^ ))^2 +(tant)^2 ))dt ∫_0 ^(2a) f(t)dt=2∫_0 ^a f(t)dt when f(2a−t)=f(t) (2/b^2 )∫_0 ^π ((d(tant))/(((a/b))^2 +(tant)^2 )) =(2/b^2 )×2∫_0 ^(π/2) ((d(tant))/(((a/b))^2 +(tant)^2 )) =(4/b^2 )×(1/(((a/b))))×∣tan^(−1) (((tant)/(a/b)))∣_0 ^(π/2) =(4/(ab))×[tan^(−1) (∞)−tan^(−1) (0)] =(4/(ab))×(π/2)=((2π)/(ab))
$$\int_{\mathrm{0}} ^{\mathrm{2}\pi} \frac{{sec}^{\mathrm{2}} {t}}{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} {tan}^{\mathrm{2}} {t}}{dt} \\ $$$$\frac{\mathrm{1}}{{b}^{\mathrm{2}} }\int_{\mathrm{0}} ^{\mathrm{2}\pi} \frac{{d}\left({tant}\right)}{\left(\frac{{a}}{{b}^{} }\right)^{\mathrm{2}} +\left({tant}\right)^{\mathrm{2}} }{dt} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{2}{a}} {f}\left({t}\right){dt}=\mathrm{2}\int_{\mathrm{0}} ^{{a}} {f}\left({t}\right){dt}\:\:{when}\:{f}\left(\mathrm{2}{a}−{t}\right)={f}\left({t}\right) \\ $$$$\frac{\mathrm{2}}{{b}^{\mathrm{2}} }\int_{\mathrm{0}} ^{\pi} \frac{{d}\left({tant}\right)}{\left(\frac{{a}}{{b}}\right)^{\mathrm{2}} +\left({tant}\right)^{\mathrm{2}} } \\ $$$$=\frac{\mathrm{2}}{{b}^{\mathrm{2}} }×\mathrm{2}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{d}\left({tant}\right)}{\left(\frac{{a}}{{b}}\right)^{\mathrm{2}} +\left({tant}\right)^{\mathrm{2}} } \\ $$$$=\frac{\mathrm{4}}{{b}^{\mathrm{2}} }×\frac{\mathrm{1}}{\left(\frac{{a}}{{b}}\right)}×\mid{tan}^{−\mathrm{1}} \left(\frac{{tant}}{\frac{{a}}{{b}}}\right)\mid_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \\ $$$$=\frac{\mathrm{4}}{{ab}}×\left[{tan}^{−\mathrm{1}} \left(\infty\right)−{tan}^{−\mathrm{1}} \left(\mathrm{0}\right)\right] \\ $$$$=\frac{\mathrm{4}}{{ab}}×\frac{\pi}{\mathrm{2}}=\frac{\mathrm{2}\pi}{{ab}} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *