Question Number 37404 by ajfour last updated on 12/Jun/18
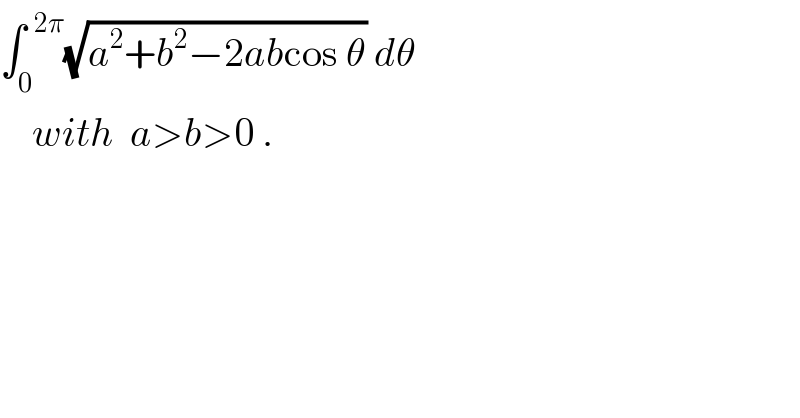
$$\int_{\mathrm{0}} ^{\:\:\mathrm{2}\pi} \sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} −\mathrm{2}{ab}\mathrm{cos}\:\theta}\:{d}\theta\: \\ $$$$\:\:\:\:{with}\:\:{a}>{b}>\mathrm{0}\:. \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 13/Jun/18

$$\int_{\mathrm{0}} ^{\mathrm{2}\Pi} \sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} −\mathrm{2}{ab}+\mathrm{2}{ab}−\mathrm{2}{abcos}\theta}\:{d}\theta \\ $$$$\int_{\mathrm{0}} ^{\mathrm{2}\Pi} \sqrt{\left({a}−{b}\right)^{\mathrm{2}} +\mathrm{2}{ab}×\mathrm{2}{sin}^{\mathrm{2}} \frac{\theta}{\mathrm{2}}}\:{d}\theta \\ $$$$\int_{\mathrm{0}} ^{\mathrm{2}\Pi} \sqrt{\left({a}−{b}\right)^{\mathrm{2}} +\left(\mathrm{2}\sqrt{{ab}}\:\right)^{\mathrm{2}} {sin}^{\mathrm{2}} \theta}{d}\theta \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}\sqrt{{ab}}\:}\int_{\mathrm{0}} ^{\mathrm{2}\Pi} \sqrt{{k}^{\mathrm{2}} +{sin}^{\mathrm{2}} \theta}\:{d}\theta\:\:\left\{{k}=\frac{\left({a}−{b}\right)}{\mathrm{2}\sqrt{{ab}}\:}\right\} \\ $$$${another}\:{way}… \\ $$$${the}\:{vslue}\:{of}\:{cos}\theta\:{lies}\:{between}\:\pm\mathrm{1} \\ $$$$\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} −\mathrm{2}{ab}}<\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} −\mathrm{2}{abcos}\theta}\:\:<\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} +\mathrm{2}{ab}} \\ $$$$\left({a}−{b}\right)\int_{\mathrm{0}} ^{\mathrm{2}\Pi} {d}\theta<{I}<\left({a}+{b}\right)\int_{\mathrm{0}} ^{\mathrm{2}\Pi} {d}\theta \\ $$$$\left({a}−{b}\right)×\mathrm{2}\Pi<{I}<\left({a}+{b}\right)×\mathrm{2}\Pi \\ $$
