Menu Close

0-2pi-a-2-sin-2-d-a-2-sin-2-b-2-cos-2-

Tinku Tara 0 Comments
Pin




Question Number 37451 by ajfour last updated on 13/Jun/18
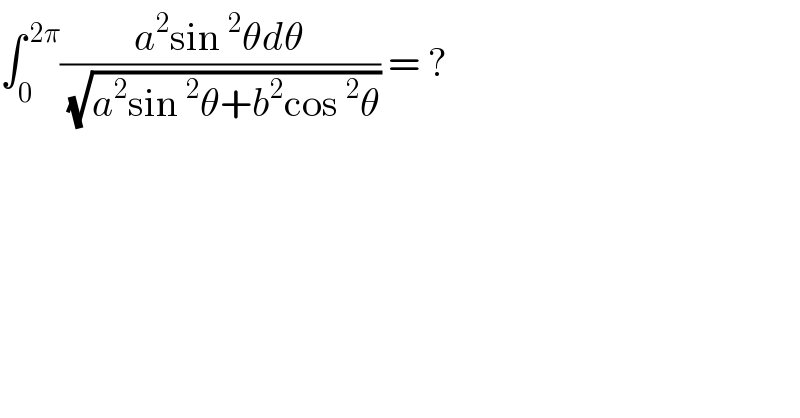
∫_0 ^( 2π) ((a^2 sin^2 θdθ)/( (√(a^2 sin^2 θ+b^2 cos^2 θ)))) = ?
$$\int_{\mathrm{0}} ^{\:\mathrm{2}\pi} \frac{{a}^{\mathrm{2}} \mathrm{sin}\:^{\mathrm{2}} \theta{d}\theta}{\:\sqrt{{a}^{\mathrm{2}} \mathrm{sin}\:^{\mathrm{2}} \theta+{b}^{\mathrm{2}} \mathrm{cos}\:^{\mathrm{2}} \theta}}\:=\:? \\ $$
Commented by MJS last updated on 13/Jun/18
this (like some others you posted) leads to an elliptic integral. see wikipedia for more info. elliptic integrals cannot be solved to elementar functions. it′s also not possible to exactly calculate the perimeter of an ellipse
$$\mathrm{this}\:\left(\mathrm{like}\:\mathrm{some}\:\mathrm{others}\:\mathrm{you}\:\mathrm{posted}\right)\:\mathrm{leads}\:\mathrm{to} \\ $$$$\mathrm{an}\:\mathrm{elliptic}\:\mathrm{integral}.\:\mathrm{see}\:\mathrm{wikipedia}\:\mathrm{for}\:\mathrm{more} \\ $$$$\mathrm{info}.\:\mathrm{elliptic}\:\mathrm{integrals}\:\mathrm{cannot}\:\mathrm{be}\:\mathrm{solved}\:\mathrm{to} \\ $$$$\mathrm{elementar}\:\mathrm{functions}.\:\mathrm{it}'\mathrm{s}\:\mathrm{also}\:\mathrm{not}\:\mathrm{possible} \\ $$$$\mathrm{to}\:\mathrm{exactly}\:\mathrm{calculate}\:\mathrm{the}\:\mathrm{perimeter}\:\mathrm{of}\:\mathrm{an} \\ $$$$\mathrm{ellipse} \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 13/Jun/18
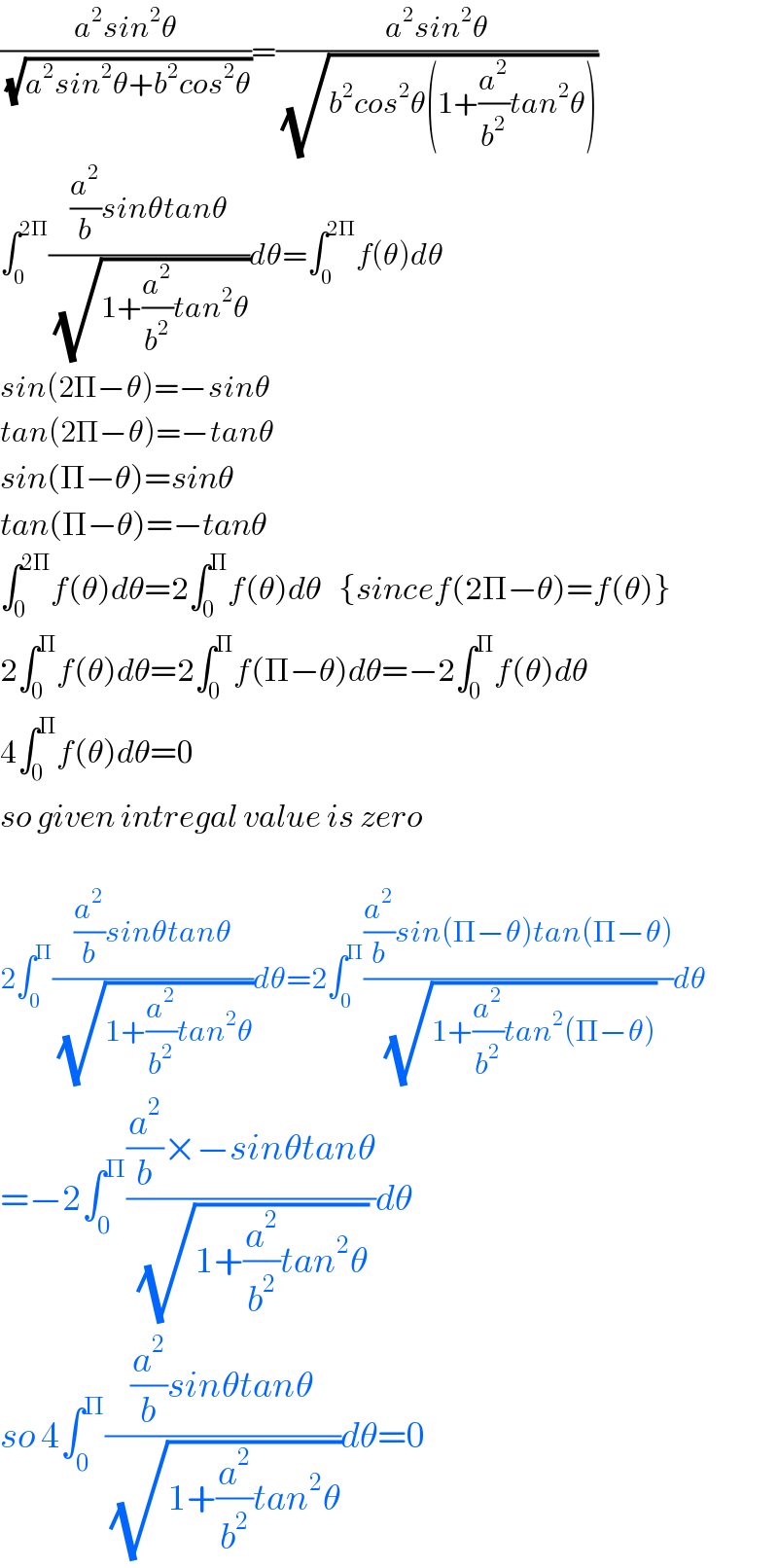
((a^2 sin^2 θ)/( (√(a^2 sin^2 θ+b^2 cos^2 θ))))=((a^2 sin^2 θ)/( (√(b^2 cos^2 θ(1+(a^2 /b^2 )tan^2 θ))))) ∫_0 ^(2Π) (((a^2 /b)sinθtanθ)/( (√(1+(a^2 /b^2 )tan^2 θ))))dθ=∫_0 ^(2Π) f(θ)dθ sin(2Π−θ)=−sinθ tan(2Π−θ)=−tanθ sin(Π−θ)=sinθ tan(Π−θ)=−tanθ ∫_0 ^(2Π) f(θ)dθ=2∫_0 ^Π f(θ)dθ {sincef(2Π−θ)=f(θ)} 2∫_0 ^Π f(θ)dθ=2∫_0 ^Π f(Π−θ)dθ=−2∫_0 ^Π f(θ)dθ 4∫_0 ^Π f(θ)dθ=0 so given intregal value is zero 2∫_0 ^Π (((a^2 /b)sinθtanθ)/( (√(1+(a^2 /b^2 )tan^2 θ))))dθ=2∫_0 ^Π (((a^2 /b)sin(Π−θ)tan(Π−θ))/( (√(1+(a^2 /b^2 )tan^2 (Π−θ)))))dθ =−2∫_0 ^Π (((a^2 /b)×−sinθtanθ)/( (√(1+(a^2 /b^2 )tan^2 θ))))dθ so 4∫_0 ^Π (((a^2 /b)sinθtanθ)/( (√(1+(a^2 /b^2 )tan^2 θ))))dθ=0
$$\frac{{a}^{\mathrm{2}} {sin}^{\mathrm{2}} \theta}{\:\sqrt{{a}^{\mathrm{2}} {sin}^{\mathrm{2}} \theta+{b}^{\mathrm{2}} {cos}^{\mathrm{2}} \theta}}=\frac{{a}^{\mathrm{2}} {sin}^{\mathrm{2}} \theta}{\:\sqrt{{b}^{\mathrm{2}} {cos}^{\mathrm{2}} \theta\left(\mathrm{1}+\frac{{a}^{\mathrm{2}} }{{b}^{\mathrm{2}} }{tan}^{\mathrm{2}} \theta\right)}} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{2}\Pi} \frac{\frac{{a}^{\mathrm{2}} }{{b}}{sin}\theta{tan}\theta}{\:\sqrt{\mathrm{1}+\frac{{a}^{\mathrm{2}} }{{b}^{\mathrm{2}} }{tan}^{\mathrm{2}} \theta}}{d}\theta=\int_{\mathrm{0}} ^{\mathrm{2}\Pi} {f}\left(\theta\right){d}\theta \\ $$$${sin}\left(\mathrm{2}\Pi−\theta\right)=−{sin}\theta \\ $$$${tan}\left(\mathrm{2}\Pi−\theta\right)=−{tan}\theta \\ $$$${sin}\left(\Pi−\theta\right)={sin}\theta \\ $$$${tan}\left(\Pi−\theta\right)=−{tan}\theta \\ $$$$\int_{\mathrm{0}} ^{\mathrm{2}\Pi} {f}\left(\theta\right){d}\theta=\mathrm{2}\int_{\mathrm{0}} ^{\Pi} {f}\left(\theta\right){d}\theta\:\:\:\left\{{sincef}\left(\mathrm{2}\Pi−\theta\right)={f}\left(\theta\right)\right\} \\ $$$$\mathrm{2}\int_{\mathrm{0}} ^{\Pi} {f}\left(\theta\right){d}\theta=\mathrm{2}\int_{\mathrm{0}} ^{\Pi} {f}\left(\Pi−\theta\right){d}\theta=−\mathrm{2}\int_{\mathrm{0}} ^{\Pi} {f}\left(\theta\right){d}\theta \\ $$$$\mathrm{4}\int_{\mathrm{0}} ^{\Pi} {f}\left(\theta\right){d}\theta=\mathrm{0} \\ $$$${so}\:{given}\:{intregal}\:{value}\:{is}\:{zero} \\ $$$$ \\ $$$$\mathrm{2}\int_{\mathrm{0}} ^{\Pi} \frac{\frac{{a}^{\mathrm{2}} }{{b}}{sin}\theta{tan}\theta}{\:\sqrt{\mathrm{1}+\frac{{a}^{\mathrm{2}} }{{b}^{\mathrm{2}} }{tan}^{\mathrm{2}} \theta}}{d}\theta=\mathrm{2}\int_{\mathrm{0}} ^{\Pi} \frac{\frac{{a}^{\mathrm{2}} }{{b}}{sin}\left(\Pi−\theta\right){tan}\left(\Pi−\theta\right)}{\:\sqrt{\mathrm{1}+\frac{{a}^{\mathrm{2}} }{{b}^{\mathrm{2}} }{tan}^{\mathrm{2}} \left(\Pi−\theta\right)}}{d}\theta \\ $$$$=−\mathrm{2}\int_{\mathrm{0}} ^{\Pi} \frac{\frac{{a}^{\mathrm{2}} }{{b}}×−{sin}\theta{tan}\theta}{\:\sqrt{\mathrm{1}+\frac{{a}^{\mathrm{2}} }{{b}^{\mathrm{2}} }{tan}^{\mathrm{2}} \theta}}{d}\theta \\ $$$${so}\:\mathrm{4}\int_{\mathrm{0}} ^{\Pi} \frac{\frac{{a}^{\mathrm{2}} }{{b}}{sin}\theta{tan}\theta}{\:\sqrt{\mathrm{1}+\frac{{a}^{\mathrm{2}} }{{b}^{\mathrm{2}} }{tan}^{\mathrm{2}} \theta}}{d}\theta=\mathrm{0} \\ $$
Commented by ajfour last updated on 13/Jun/18
should not be !
$${should}\:{not}\:{be}\:! \\ $$
Commented by ajfour last updated on 13/Jun/18
((a^2 sin^2 θ)/( (√(b^2 cos^2 θ(1+(a^2 /b^2 )tan^2 θ))))) =((a^2 sin^2 θ)/(∣bcos θ∣(√(1+(a^2 /b^2 )tan^2 θ)))) =((a^2 ∣sin θ tan θ∣)/(b(√(1+(a^2 /b^2 )tan^2 θ)))) .....
$$\frac{{a}^{\mathrm{2}} {sin}^{\mathrm{2}} \theta}{\:\sqrt{{b}^{\mathrm{2}} {cos}^{\mathrm{2}} \theta\left(\mathrm{1}+\frac{{a}^{\mathrm{2}} }{{b}^{\mathrm{2}} }{tan}^{\mathrm{2}} \theta\right)}} \\ $$$$=\frac{{a}^{\mathrm{2}} \mathrm{sin}\:^{\mathrm{2}} \theta}{\mid{b}\mathrm{cos}\:\theta\mid\sqrt{\mathrm{1}+\frac{{a}^{\mathrm{2}} }{{b}^{\mathrm{2}} }\mathrm{tan}\:^{\mathrm{2}} \theta}} \\ $$$$=\frac{{a}^{\mathrm{2}} \mid\mathrm{sin}\:\theta\:\mathrm{tan}\:\theta\mid}{{b}\sqrt{\mathrm{1}+\frac{{a}^{\mathrm{2}} }{{b}^{\mathrm{2}} }\mathrm{tan}\:^{\mathrm{2}} \theta}} \\ $$$$….. \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 13/Jun/18
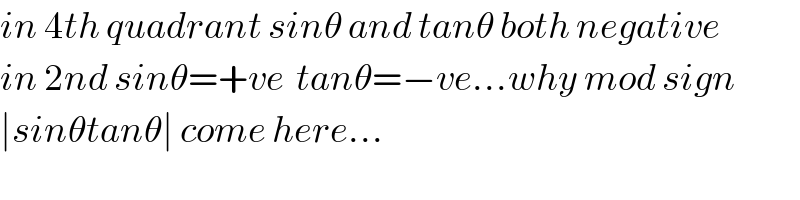
in 4th quadrant sinθ and tanθ both negative in 2nd sinθ=+ve tanθ=−ve...why mod sign ∣sinθtanθ∣ come here...
$${in}\:\mathrm{4}{th}\:{quadrant}\:{sin}\theta\:{and}\:{tan}\theta\:{both}\:{negative} \\ $$$${in}\:\mathrm{2}{nd}\:{sin}\theta=+{ve}\:\:{tan}\theta=−{ve}…{why}\:{mod}\:{sign} \\ $$$$\mid{sin}\theta{tan}\theta\mid\:{come}\:{here}… \\ $$
Commented by ajfour last updated on 13/Jun/18
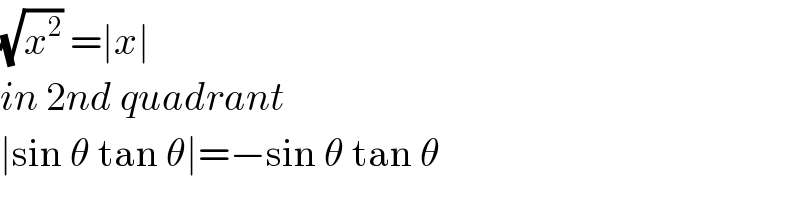
(√x^2 ) =∣x∣ in 2nd quadrant ∣sin θ tan θ∣=−sin θ tan θ
$$\sqrt{{x}^{\mathrm{2}} }\:=\mid{x}\mid \\ $$$${in}\:\mathrm{2}{nd}\:{quadrant} \\ $$$$\mid\mathrm{sin}\:\theta\:\mathrm{tan}\:\theta\mid=−\mathrm{sin}\:\theta\:\mathrm{tan}\:\theta \\ $$
Answered by ajfour last updated on 14/Jun/18
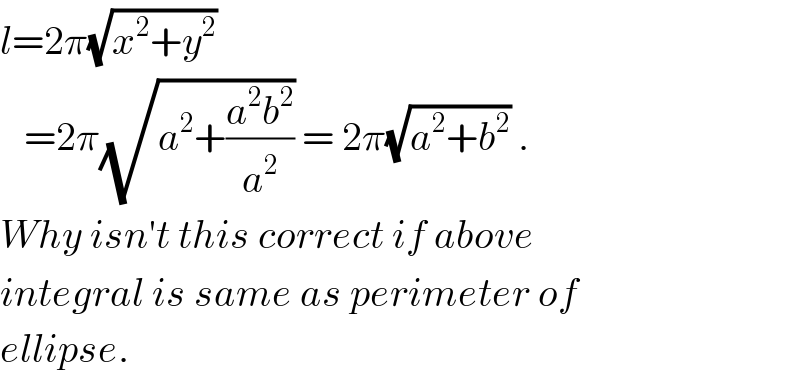
l=2π(√(x^2 +y^2 )) =2π(√(a^2 +((a^2 b^2 )/a^2 ))) = 2π(√(a^2 +b^2 )) . Why isn′t this correct if above integral is same as perimeter of ellipse.
$${l}=\mathrm{2}\pi\sqrt{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} } \\ $$$$\:\:\:=\mathrm{2}\pi\sqrt{{a}^{\mathrm{2}} +\frac{{a}^{\mathrm{2}} {b}^{\mathrm{2}} }{{a}^{\mathrm{2}} }}\:=\:\mathrm{2}\pi\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }\:. \\ $$$${Why}\:{isn}'{t}\:{this}\:{correct}\:{if}\:{above} \\ $$$${integral}\:{is}\:{same}\:{as}\:{perimeter}\:{of} \\ $$$${ellipse}.\: \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *