Menu Close

0-2pi-cos-1-cos-x-dx-

Tinku Tara 0 Comments
Pin




Question Number 151276 by peter frank last updated on 19/Aug/21
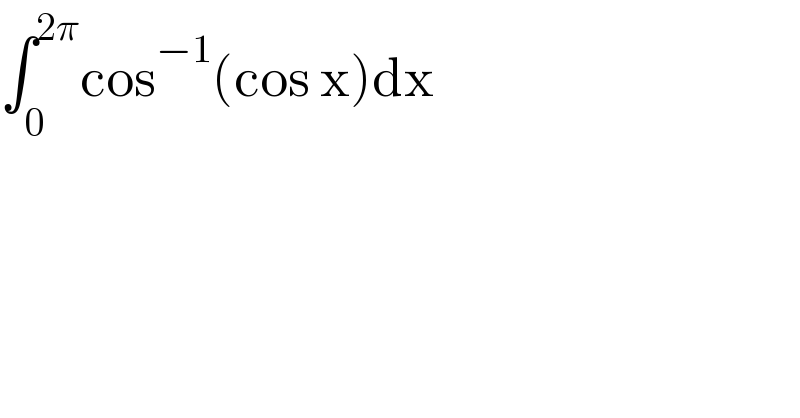
∫_0 ^(2π) cos^(−1) (cos x)dx
$$\int_{\mathrm{0}} ^{\mathrm{2}\pi} \mathrm{cos}^{−\mathrm{1}} \left(\mathrm{cos}\:\mathrm{x}\right)\mathrm{dx} \\ $$
Commented by tabata last updated on 19/Aug/21
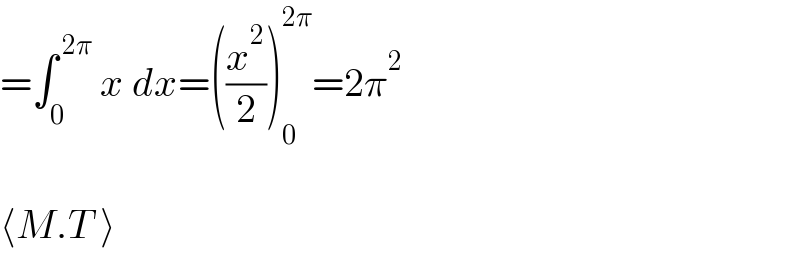
=∫_0 ^( 2π) x dx=((x^2 /2))_0 ^(2π) =2π^2 ⟨M.T ⟩
$$=\int_{\mathrm{0}} ^{\:\mathrm{2}\pi} \:{x}\:{dx}=\left(\frac{{x}^{\mathrm{2}} }{\mathrm{2}}\right)_{\mathrm{0}} ^{\mathrm{2}\pi} =\mathrm{2}\pi^{\mathrm{2}} \\ $$$$ \\ $$$$\langle{M}.{T}\:\rangle \\ $$
Commented by peter frank last updated on 19/Aug/21
thank you
$$\mathrm{thank}\:\mathrm{you} \\ $$
Answered by MJS_new last updated on 19/Aug/21
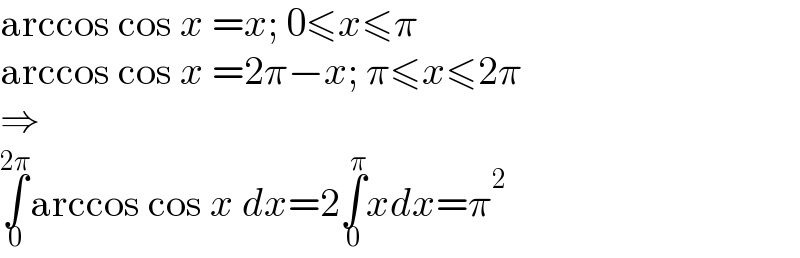
arccos cos x =x; 0≤x≤π arccos cos x =2π−x; π≤x≤2π ⇒ ∫_0 ^(2π) arccos cos x dx=2∫_0 ^π xdx=π^2
$$\mathrm{arccos}\:\mathrm{cos}\:{x}\:={x};\:\mathrm{0}\leqslant{x}\leqslant\pi \\ $$$$\mathrm{arccos}\:\mathrm{cos}\:{x}\:=\mathrm{2}\pi−{x};\:\pi\leqslant{x}\leqslant\mathrm{2}\pi \\ $$$$\Rightarrow \\ $$$$\underset{\mathrm{0}} {\overset{\mathrm{2}\pi} {\int}}\mathrm{arccos}\:\mathrm{cos}\:{x}\:{dx}=\mathrm{2}\underset{\mathrm{0}} {\overset{\pi} {\int}}{xdx}=\pi^{\mathrm{2}} \\ $$
Commented by peter frank last updated on 19/Aug/21
thank you
$$\mathrm{thank}\:\mathrm{you} \\ $$
Commented by peter frank last updated on 19/Aug/21
arcsin sin x?,arctantanx?
$$\mathrm{arcsin}\:\mathrm{sin}\:\mathrm{x}?,\mathrm{arctantanx}? \\ $$
Answered by mathmax by abdo last updated on 19/Aug/21
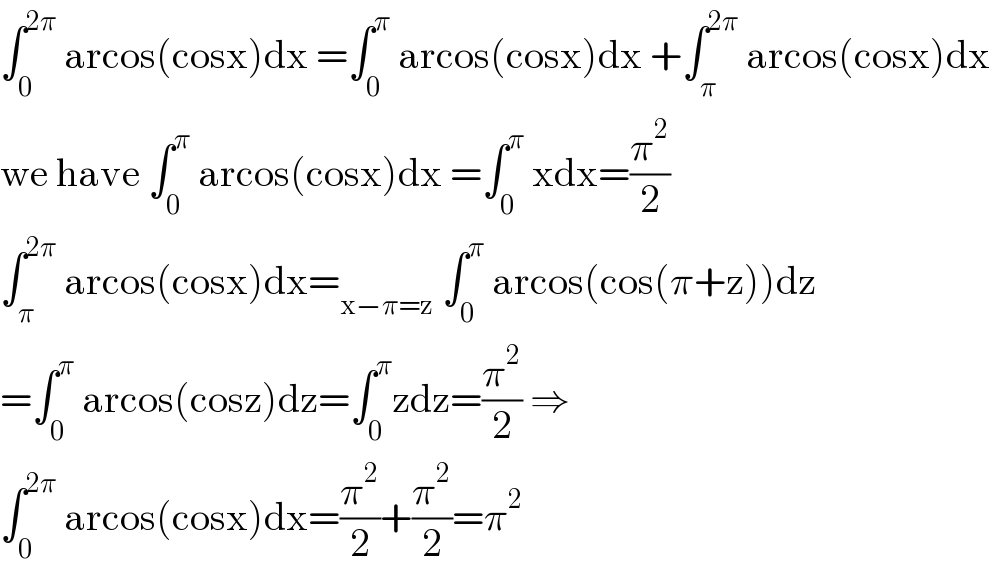
∫_0 ^(2π) arcos(cosx)dx =∫_0 ^π arcos(cosx)dx +∫_π ^(2π) arcos(cosx)dx we have ∫_0 ^π arcos(cosx)dx =∫_0 ^π xdx=(π^2 /2) ∫_π ^(2π) arcos(cosx)dx=_(x−π=z) ∫_0 ^π arcos(cos(π+z))dz =∫_0 ^π arcos(cosz)dz=∫_0 ^π zdz=(π^2 /2) ⇒ ∫_0 ^(2π) arcos(cosx)dx=(π^2 /2)+(π^2 /2)=π^2
$$\int_{\mathrm{0}} ^{\mathrm{2}\pi} \:\mathrm{arcos}\left(\mathrm{cosx}\right)\mathrm{dx}\:=\int_{\mathrm{0}} ^{\pi} \:\mathrm{arcos}\left(\mathrm{cosx}\right)\mathrm{dx}\:+\int_{\pi} ^{\mathrm{2}\pi} \:\mathrm{arcos}\left(\mathrm{cosx}\right)\mathrm{dx} \\ $$$$\mathrm{we}\:\mathrm{have}\:\int_{\mathrm{0}} ^{\pi} \:\mathrm{arcos}\left(\mathrm{cosx}\right)\mathrm{dx}\:=\int_{\mathrm{0}} ^{\pi} \:\mathrm{xdx}=\frac{\pi^{\mathrm{2}} }{\mathrm{2}} \\ $$$$\int_{\pi} ^{\mathrm{2}\pi} \:\mathrm{arcos}\left(\mathrm{cosx}\right)\mathrm{dx}=_{\mathrm{x}−\pi=\mathrm{z}} \:\int_{\mathrm{0}} ^{\pi} \:\mathrm{arcos}\left(\mathrm{cos}\left(\pi+\mathrm{z}\right)\right)\mathrm{dz} \\ $$$$=\int_{\mathrm{0}} ^{\pi} \:\mathrm{arcos}\left(\mathrm{cosz}\right)\mathrm{dz}=\int_{\mathrm{0}} ^{\pi} \mathrm{zdz}=\frac{\pi^{\mathrm{2}} }{\mathrm{2}}\:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\mathrm{2}\pi} \:\mathrm{arcos}\left(\mathrm{cosx}\right)\mathrm{dx}=\frac{\pi^{\mathrm{2}} }{\mathrm{2}}+\frac{\pi^{\mathrm{2}} }{\mathrm{2}}=\pi^{\mathrm{2}} \\ $$
Commented by peter frank last updated on 19/Aug/21
thank you
$$\mathrm{thank}\:\mathrm{you} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *