Question Number 93109 by Mikael_786 last updated on 10/May/20
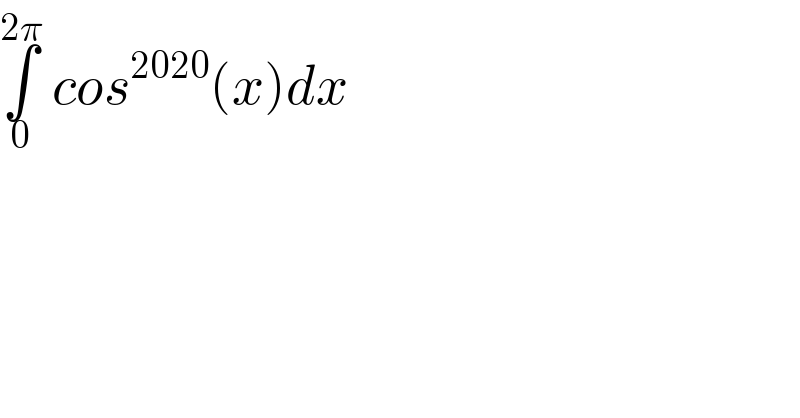
$$\underset{\mathrm{0}} {\overset{\mathrm{2}\pi} {\int}}\:{cos}^{\mathrm{2020}} \left({x}\right){dx} \\ $$
Commented by prakash jain last updated on 11/May/20
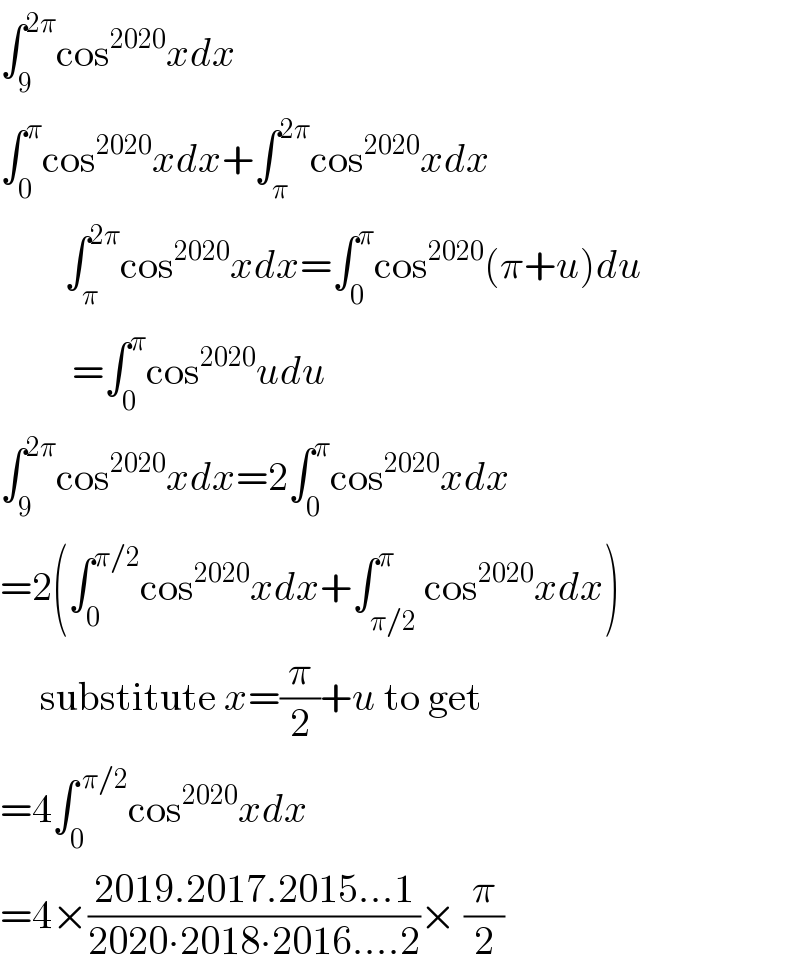
$$\int_{\mathrm{9}} ^{\mathrm{2}\pi} \mathrm{cos}^{\mathrm{2020}} {xdx} \\ $$$$\int_{\mathrm{0}} ^{\pi} \mathrm{cos}^{\mathrm{2020}} {xdx}+\int_{\pi} ^{\mathrm{2}\pi} \mathrm{cos}^{\mathrm{2020}} {xdx} \\ $$$$\:\:\:\:\:\:\:\:\int_{\pi} ^{\mathrm{2}\pi} \mathrm{cos}^{\mathrm{2020}} {xdx}=\int_{\mathrm{0}} ^{\pi} \mathrm{cos}^{\mathrm{2020}} \left(\pi+{u}\right){du} \\ $$$$\:\:\:\:\:\:\:\:\:=\int_{\mathrm{0}} ^{\pi} \mathrm{cos}^{\mathrm{2020}} {udu} \\ $$$$\int_{\mathrm{9}} ^{\mathrm{2}\pi} \mathrm{cos}^{\mathrm{2020}} {xdx}=\mathrm{2}\int_{\mathrm{0}} ^{\pi} \mathrm{cos}^{\mathrm{2020}} {xdx} \\ $$$$=\mathrm{2}\left(\int_{\mathrm{0}} ^{\pi/\mathrm{2}} \mathrm{cos}^{\mathrm{2020}} {xdx}+\int_{\pi/\mathrm{2}} ^{\pi} \mathrm{cos}^{\mathrm{2020}} {xdx}\right) \\ $$$$\:\:\:\:\:\mathrm{substitute}\:{x}=\frac{\pi}{\mathrm{2}}+{u}\:\mathrm{to}\:\mathrm{get} \\ $$$$=\mathrm{4}\int_{\mathrm{0}} ^{\:\pi/\mathrm{2}} \mathrm{cos}^{\mathrm{2020}} {xdx} \\ $$$$=\mathrm{4}×\frac{\mathrm{2019}.\mathrm{2017}.\mathrm{2015}…\mathrm{1}}{\mathrm{2020}\centerdot\mathrm{2018}\centerdot\mathrm{2016}….\mathrm{2}}×\:\frac{\pi}{\mathrm{2}} \\ $$
Commented by Mikael_786 last updated on 10/May/20

$${thank}\:{u}\:{Sir} \\ $$
