Question Number 45063 by rahul 19 last updated on 08/Oct/18
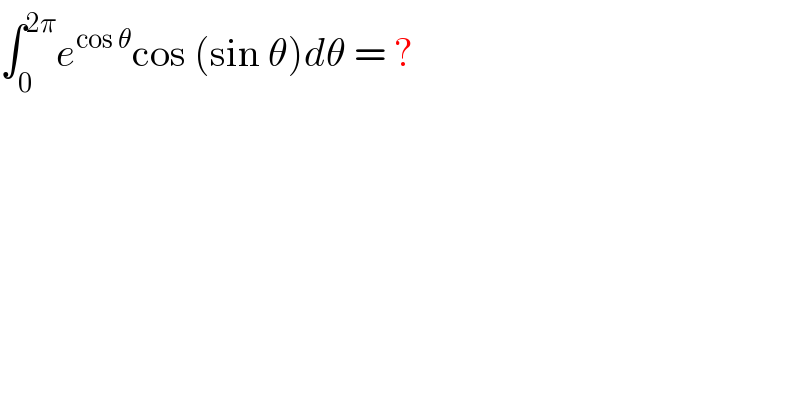
$$\int_{\mathrm{0}} ^{\mathrm{2}\pi} {e}^{\mathrm{cos}\:\theta} \mathrm{cos}\:\left(\mathrm{sin}\:\theta\right){d}\theta\:=\:? \\ $$
Commented by maxmathsup by imad last updated on 08/Oct/18
![I =Re( ∫_0 ^(2π) e^(cosθ+isinθ) dθ) but e^(cosθ+isinθ) =e^e^(iθ) =Σ_(n=0) ^∞ (((e^(iθ) )^n )/(n!)) =Σ_(n=0) ^∞ (e^(inθ) /(n!)) =Σ_(n=0) ^∞ ((cos(nθ))/(n!)) +i Σ_(n=0) ^∞ ((sin(nθ))/(n!)) ⇒ ∫_0 ^(2π) e^e^(iθ) dθ =Σ_(n=0) ^∞ (1/(n!))∫_0 ^(2π) cos(nθ)dθ +i Σ_(n=0) ^∞ (1/(n!)) ∫_0 ^(2π) sin(nθ)dθ =2π +Σ_(n=1) ^∞ ∫_0 ^(2π) cos(nθ)dθ +iΣ_(n=1) ^∞ (1/(n!)) ∫_0 ^(2π) sin(nθ)dθ but ∫_0 ^(2π) cos(nθ)dθ =[(1/n)sin(nθ)]_0 ^(2π) =0 (n≥1) also ∫_0 ^(2π) sin(nθ)dθ =[−(1/n)cos(nθ)]_0 ^(2π) =0 (n≥1) ⇒∫_0 ^(2π) e^e^(iθ) dθ =2π ⇒ ∫_0 ^(2π) e^(cosθ) cos(sinθ)dθ =2π .](https://www.tinkutara.com/question/Q45071.png)
$${I}\:={Re}\left(\:\int_{\mathrm{0}} ^{\mathrm{2}\pi} \:{e}^{{cos}\theta+{isin}\theta} {d}\theta\right)\:\:{but}\:{e}^{{cos}\theta+{isin}\theta} \:={e}^{{e}^{{i}\theta} } \:=\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{\left({e}^{{i}\theta} \right)^{{n}} }{{n}!} \\ $$$$=\sum_{{n}=\mathrm{0}} ^{\infty} \:\:\:\frac{{e}^{{in}\theta} }{{n}!}\:=\sum_{{n}=\mathrm{0}} ^{\infty} \:\:\frac{{cos}\left({n}\theta\right)}{{n}!}\:+{i}\:\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{{sin}\left({n}\theta\right)}{{n}!}\:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\mathrm{2}\pi} \:{e}^{{e}^{{i}\theta} } {d}\theta\:=\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{1}}{{n}!}\int_{\mathrm{0}} ^{\mathrm{2}\pi} {cos}\left({n}\theta\right){d}\theta\:+{i}\:\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{1}}{{n}!}\:\int_{\mathrm{0}} ^{\mathrm{2}\pi} \:{sin}\left({n}\theta\right){d}\theta \\ $$$$=\mathrm{2}\pi\:+\sum_{{n}=\mathrm{1}} ^{\infty} \:\int_{\mathrm{0}} ^{\mathrm{2}\pi} {cos}\left({n}\theta\right){d}\theta\:+{i}\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{1}}{{n}!}\:\int_{\mathrm{0}} ^{\mathrm{2}\pi} \:{sin}\left({n}\theta\right){d}\theta\:{but} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{2}\pi} {cos}\left({n}\theta\right){d}\theta\:=\left[\frac{\mathrm{1}}{{n}}{sin}\left({n}\theta\right)\right]_{\mathrm{0}} ^{\mathrm{2}\pi} =\mathrm{0}\:\:\left({n}\geqslant\mathrm{1}\right)\:{also} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{2}\pi} {sin}\left({n}\theta\right){d}\theta\:=\left[−\frac{\mathrm{1}}{{n}}{cos}\left({n}\theta\right)\right]_{\mathrm{0}} ^{\mathrm{2}\pi} \:=\mathrm{0}\:\left({n}\geqslant\mathrm{1}\right)\:\Rightarrow\int_{\mathrm{0}} ^{\mathrm{2}\pi} \:\:{e}^{{e}^{{i}\theta} } {d}\theta\:=\mathrm{2}\pi\:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\mathrm{2}\pi} \:{e}^{{cos}\theta} \:{cos}\left({sin}\theta\right){d}\theta\:=\mathrm{2}\pi\:. \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 08/Oct/18

