Question Number 121684 by mathocean1 last updated on 10/Nov/20
![θ ∈ [0;2π]. solve in C this equation: z^2 −(2^(θ+1) cosθ)z+2^(2θ) =0](https://www.tinkutara.com/question/Q121684.png)
$$\theta\:\in\:\left[\mathrm{0};\mathrm{2}\pi\right]. \\ $$$${solve}\:{in}\:\mathbb{C}\:{this}\:{equation}: \\ $$$${z}^{\mathrm{2}} −\left(\mathrm{2}^{\theta+\mathrm{1}} {cos}\theta\right){z}+\mathrm{2}^{\mathrm{2}\theta} =\mathrm{0} \\ $$$$ \\ $$
Commented by Dwaipayan Shikari last updated on 10/Nov/20
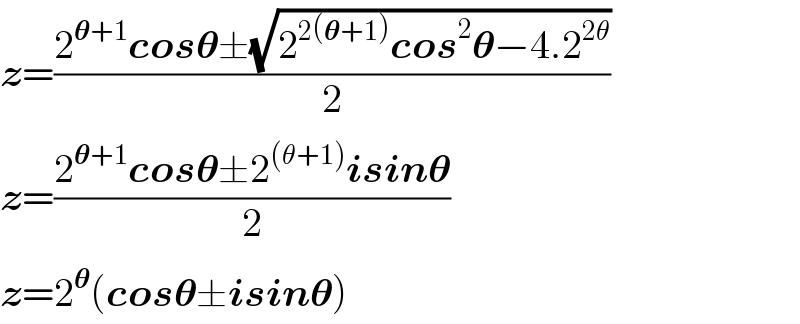
$$\boldsymbol{{z}}=\frac{\mathrm{2}^{\boldsymbol{\theta}+\mathrm{1}} \boldsymbol{{cos}\theta}\pm\sqrt{\mathrm{2}^{\mathrm{2}\left(\boldsymbol{\theta}+\mathrm{1}\right)} \boldsymbol{{cos}}^{\mathrm{2}} \boldsymbol{\theta}−\mathrm{4}.\mathrm{2}^{\mathrm{2}\theta} }}{\mathrm{2}} \\ $$$$\boldsymbol{{z}}=\frac{\mathrm{2}^{\boldsymbol{\theta}+\mathrm{1}} \boldsymbol{{cos}\theta}\pm\mathrm{2}^{\left(\theta+\mathrm{1}\right)} \boldsymbol{{isin}\theta}}{\mathrm{2}} \\ $$$$\boldsymbol{{z}}=\mathrm{2}^{\boldsymbol{\theta}} \left(\boldsymbol{{cos}\theta}\pm\boldsymbol{{isin}\theta}\right) \\ $$
