Question Number 90796 by M±th+et+s last updated on 26/Apr/20
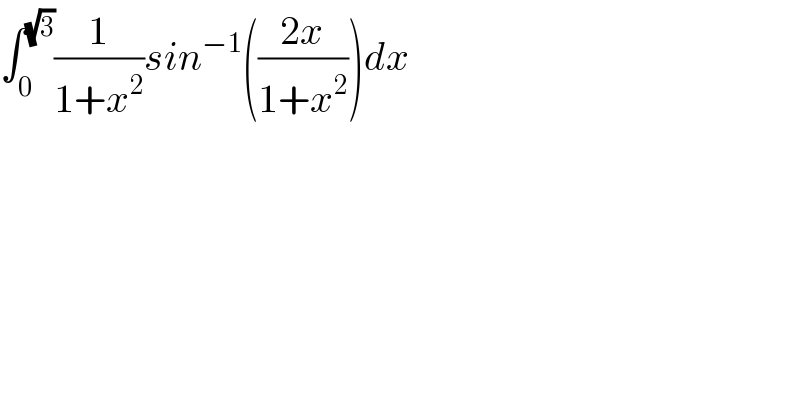
$$\int_{\mathrm{0}} ^{\sqrt{\mathrm{3}}} \frac{\mathrm{1}}{\mathrm{1}+{x}^{\mathrm{2}} }{sin}^{−\mathrm{1}} \left(\frac{\mathrm{2}{x}}{\mathrm{1}+{x}^{\mathrm{2}} }\right){dx} \\ $$
Commented by mathmax by abdo last updated on 26/Apr/20
![I =∫_0 ^(√3) (1/(1+x^2 )) arcsin(((2x)/(1+x^2 )))dx cyangement x=tanθ give I =∫_0 ^(π/3) (1/(1+tan^2 θ)) arcsin(sin(2θ))(1+tan^2 θ)dθ =∫_0 ^(π/3) 2θdθ =[θ^2 ]_0 ^(π/3) =(π^2 /9)](https://www.tinkutara.com/question/Q90891.png)
$${I}\:=\int_{\mathrm{0}} ^{\sqrt{\mathrm{3}}} \:\frac{\mathrm{1}}{\mathrm{1}+{x}^{\mathrm{2}} }\:{arcsin}\left(\frac{\mathrm{2}{x}}{\mathrm{1}+{x}^{\mathrm{2}} }\right){dx}\:\:{cyangement}\:\:{x}={tan}\theta\:{give} \\ $$$${I}\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{3}}} \:\frac{\mathrm{1}}{\mathrm{1}+{tan}^{\mathrm{2}} \theta}\:{arcsin}\left({sin}\left(\mathrm{2}\theta\right)\right)\left(\mathrm{1}+{tan}^{\mathrm{2}} \theta\right){d}\theta \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{3}}} \:\mathrm{2}\theta{d}\theta\:=\left[\theta^{\mathrm{2}} \right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{3}}} \:\:=\frac{\pi^{\mathrm{2}} }{\mathrm{9}} \\ $$
Commented by M±th+et+s last updated on 27/Apr/20
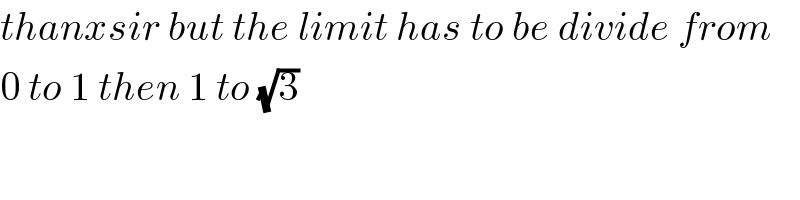
$${thanxsir}\:{but}\:{the}\:{limit}\:{has}\:{to}\:{be}\:{divide}\:{from}\: \\ $$$$\mathrm{0}\:{to}\:\mathrm{1}\:{then}\:\mathrm{1}\:{to}\:\sqrt{\mathrm{3}} \\ $$
Commented by mathmax by abdo last updated on 28/Apr/20

$${no}\:{sir}\:{the}\:{limits}\:{go}\:{from}\:{arctan}\left(\mathrm{0}\right)=\mathrm{0}\:{to}\:{arctan}\left(\sqrt{\mathrm{3}}\right)\:=\frac{\pi}{\mathrm{3}} \\ $$
Answered by TANMAY PANACEA. last updated on 26/Apr/20
![∫(1/(1+x^2 ))sin^(−1) (((2x)/(1+x^2 )))dx x=tana ∫(1/(sec^2 a))×sin^(−1) (sin2a)sec^2 a da a^2 so answer [∣tan^(−1) x∣_0 ^(√3) ]^2 →((π/3))^2 =(π^2 /9)](https://www.tinkutara.com/question/Q90797.png)
$$\int\frac{\mathrm{1}}{\mathrm{1}+{x}^{\mathrm{2}} }{sin}^{−\mathrm{1}} \left(\frac{\mathrm{2}{x}}{\mathrm{1}+{x}^{\mathrm{2}} }\right){dx} \\ $$$${x}={tana} \\ $$$$\int\frac{\mathrm{1}}{{sec}^{\mathrm{2}} {a}}×{sin}^{−\mathrm{1}} \left({sin}\mathrm{2}{a}\right){sec}^{\mathrm{2}} {a}\:{da} \\ $$$${a}^{\mathrm{2}} \\ $$$${so}\:{answer} \\ $$$$\left[\mid{tan}^{−\mathrm{1}} {x}\mid_{\mathrm{0}} ^{\sqrt{\mathrm{3}}} \:\:\right]^{\mathrm{2}} \rightarrow\left(\frac{\pi}{\mathrm{3}}\right)^{\mathrm{2}} =\frac{\pi^{\mathrm{2}} }{\mathrm{9}} \\ $$
Commented by M±th+et+s last updated on 26/Apr/20

$${i}\:{think}\:{its}\:\frac{\mathrm{7}\pi^{\mathrm{2}} }{\mathrm{72}} \\ $$
Answered by M±th+et+s last updated on 28/Apr/20
![I=∫_0 ^(π/3) (1/(1+tan^2 θ))sin^(−1) (((2tanθ)/(1+tan^2 (x))))d(tanθ) =∫_0 ^(π/3) cos^2 (θ) sin^(−1) (sin2θ)(1/(cos^2 (θ)))dθ ∫_0 ^(π/3) sin^(−1) (2θ)dθ the last tricky! sin^(−1) sinθ≠θ,θ>[(π/2)]! (1) this is because sin^(−1) (θ) to be a function it must defined as a mapping only to sub−region of R. specifically: sin^(−1) :[−1,1]→[((−π)/2),(π/2)] :x→θ=sin^(−1) (x) therefore.following gives a one to one mapping: sin^(−1) sin:[((−π)/2),(π/2)]→[((−π)/2),(π/2)] in our case the argument is 2θ so our range get coparessed by a factor of two so we get ollowing one to many mapping: sin^(−1) sin(2×_):[((−π)/4),(π/4)]→[((−π)/2),(π/2)] with a littile thought we can extand past (π/4) to (π/2) and obtain following plot of sin^(−1) sin2θ with θ∈[0,(π/2)] which is a one to many mapping: so the integral is just the area under the curve from 0 to π/3 breaking this up: ⇒for θ∈[0,(π/4)],the area of the triangle is (π^2 /(16)). ⇒for θ∈[(π/4),(π/3)],the area trapeziod is 5π^2 /144 summing these two,gives ((7π^2 )/(72)) (2)](https://www.tinkutara.com/question/Q91118.png)
$${I}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{3}}} \frac{\mathrm{1}}{\mathrm{1}+{tan}^{\mathrm{2}} \theta}{sin}^{−\mathrm{1}} \left(\frac{\mathrm{2}{tan}\theta}{\mathrm{1}+{tan}^{\mathrm{2}} \left({x}\right)}\right){d}\left({tan}\theta\right) \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{3}}} {cos}^{\mathrm{2}} \left(\theta\right)\:{sin}^{−\mathrm{1}} \left({sin}\mathrm{2}\theta\right)\frac{\mathrm{1}}{{cos}^{\mathrm{2}} \left(\theta\right)}{d}\theta \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{3}}} {sin}^{−\mathrm{1}} \left(\mathrm{2}\theta\right){d}\theta \\ $$$${the}\:{last}\:{tricky}! \\ $$$${sin}^{−\mathrm{1}} {sin}\theta\neq\theta,\theta>\left[\frac{\pi}{\mathrm{2}}\right]!\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\left(\mathrm{1}\right) \\ $$$${this}\:{is}\:{because}\:{sin}^{−\mathrm{1}} \left(\theta\right)\:{to}\:{be}\:{a}\:{function} \\ $$$${it}\:{must}\:{defined}\:{as}\:{a}\:{mapping}\:{only} \\ $$$${to}\:{sub}−{region}\:{of}\:\mathbb{R}. \\ $$$$ \\ $$$${specifically}: \\ $$$${sin}^{−\mathrm{1}} :\left[−\mathrm{1},\mathrm{1}\right]\rightarrow\left[\frac{−\pi}{\mathrm{2}},\frac{\pi}{\mathrm{2}}\right] \\ $$$$:{x}\rightarrow\theta={sin}^{−\mathrm{1}} \left({x}\right) \\ $$$${therefore}.{following}\:{gives}\:{a}\:{one}\:{to}\:{one} \\ $$$${mapping}: \\ $$$${sin}^{−\mathrm{1}} {sin}:\left[\frac{−\pi}{\mathrm{2}},\frac{\pi}{\mathrm{2}}\right]\rightarrow\left[\frac{−\pi}{\mathrm{2}},\frac{\pi}{\mathrm{2}}\right] \\ $$$${in}\:{our}\:{case}\:{the}\:{argument}\:{is}\:\mathrm{2}\theta\:{so}\:{our} \\ $$$${range}\:{get}\:{coparessed}\:{by}\:{a}\:{factor}\:{of}\:{two} \\ $$$${so}\:{we}\:{get}\:{ollowing}\:{one}\:{to}\:{many}\:{mapping}: \\ $$$${sin}^{−\mathrm{1}} {sin}\left(\mathrm{2}×\_\right):\left[\frac{−\pi}{\mathrm{4}},\frac{\pi}{\mathrm{4}}\right]\rightarrow\left[\frac{−\pi}{\mathrm{2}},\frac{\pi}{\mathrm{2}}\right] \\ $$$$ \\ $$$${with}\:{a}\:{littile}\:{thought}\:{we}\:{can}\:{extand} \\ $$$${past}\:\frac{\pi}{\mathrm{4}}\:{to}\:\frac{\pi}{\mathrm{2}}\:{and}\:{obtain}\:{following}\:{plot} \\ $$$${of}\:{sin}^{−\mathrm{1}} {sin}\mathrm{2}\theta\:{with}\:\theta\in\left[\mathrm{0},\frac{\pi}{\mathrm{2}}\right]\:{which} \\ $$$${is}\:{a}\:{one}\:{to}\:{many}\:{mapping}: \\ $$$$ \\ $$$${so}\:{the}\:{integral}\:{is}\:{just}\:{the}\:{area}\:{under} \\ $$$${the}\:{curve}\:{from}\:\mathrm{0}\:{to}\:\pi/\mathrm{3}\:{breaking}\:{this} \\ $$$${up}: \\ $$$$\Rightarrow{for}\:\theta\in\left[\mathrm{0},\frac{\pi}{\mathrm{4}}\right],{the}\:{area}\:{of}\:{the}\:{triangle} \\ $$$${is}\:\frac{\pi^{\mathrm{2}} }{\mathrm{16}}. \\ $$$$\Rightarrow{for}\:\theta\in\left[\frac{\pi}{\mathrm{4}},\frac{\pi}{\mathrm{3}}\right],{the}\:{area}\:{trapeziod}\: \\ $$$${is}\:\mathrm{5}\pi^{\mathrm{2}} /\mathrm{144} \\ $$$${summing}\:{these}\:{two},{gives} \\ $$$$\frac{\mathrm{7}\pi^{\mathrm{2}} }{\mathrm{72}}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\left(\mathrm{2}\right) \\ $$$$ \\ $$
