Question Number 122542 by bramlexs22 last updated on 18/Nov/20
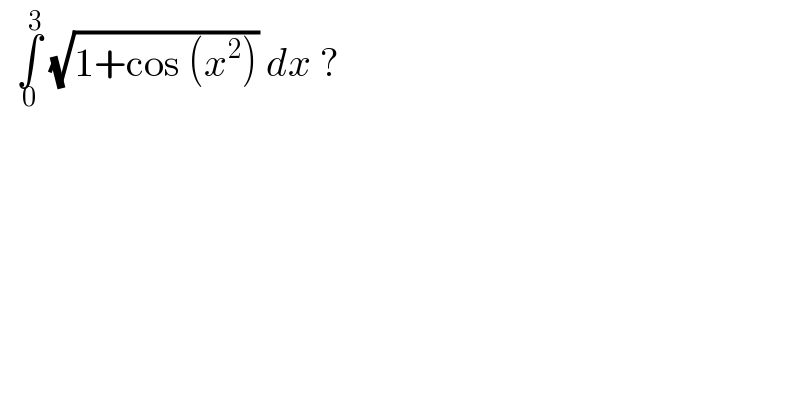
$$\:\:\underset{\mathrm{0}} {\overset{\mathrm{3}} {\int}}\:\sqrt{\mathrm{1}+\mathrm{cos}\:\left({x}^{\mathrm{2}} \right)}\:{dx}\:? \\ $$
Answered by Olaf last updated on 18/Nov/20
![I = ∫_0 ^3 (√(1+cos(x^2 )))dx I = ∫_0 ^3 (√(2cos^2 ((x^2 /2))))dx I = (√2)∫_0 ^3 ∣cos((x^2 /2))∣dx I = (√2)∫_0 ^(√π) ∣cos((x^2 /2))∣dx+(√2)∫_(√π) ^3 ∣cos^2 ((x^2 /2))∣dx I = (√2)∫_0 ^(√π) cos((x^2 /2))dx−(√2)∫_(√π) ^3 cos^2 ((x^2 /2))dx I = (√2)[(√π)FresnelC((x/π))]_0 ^(√π) −(√2)[(√π)FresnelC((x/π))]_(√π) ^3 I = (√(2π))[2FresnelC((1/( (√π))))−FresnelC(0)−FresnelC(3)] I = (√(2π))[2FresnelC((1/( (√π))))−FresnelC(3)] Note : Fresnel Cosine Integral FresnelC(z) = ∫_0 ^z cos(((πt^2 )/2))dt](https://www.tinkutara.com/question/Q122616.png)
$$\mathrm{I}\:=\:\int_{\mathrm{0}} ^{\mathrm{3}} \sqrt{\mathrm{1}+\mathrm{cos}\left({x}^{\mathrm{2}} \right)}{dx} \\ $$$$\mathrm{I}\:=\:\int_{\mathrm{0}} ^{\mathrm{3}} \sqrt{\mathrm{2cos}^{\mathrm{2}} \left(\frac{{x}^{\mathrm{2}} }{\mathrm{2}}\right)}{dx} \\ $$$$\mathrm{I}\:=\:\sqrt{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{3}} \mid\mathrm{cos}\left(\frac{{x}^{\mathrm{2}} }{\mathrm{2}}\right)\mid{dx} \\ $$$$\mathrm{I}\:=\:\sqrt{\mathrm{2}}\int_{\mathrm{0}} ^{\sqrt{\pi}} \mid\mathrm{cos}\left(\frac{{x}^{\mathrm{2}} }{\mathrm{2}}\right)\mid{dx}+\sqrt{\mathrm{2}}\int_{\sqrt{\pi}} ^{\mathrm{3}} \mid\mathrm{cos}^{\mathrm{2}} \left(\frac{{x}^{\mathrm{2}} }{\mathrm{2}}\right)\mid{dx} \\ $$$$\mathrm{I}\:=\:\sqrt{\mathrm{2}}\int_{\mathrm{0}} ^{\sqrt{\pi}} \mathrm{cos}\left(\frac{{x}^{\mathrm{2}} }{\mathrm{2}}\right){dx}−\sqrt{\mathrm{2}}\int_{\sqrt{\pi}} ^{\mathrm{3}} \mathrm{cos}^{\mathrm{2}} \left(\frac{{x}^{\mathrm{2}} }{\mathrm{2}}\right){dx} \\ $$$$\mathrm{I}\:=\:\sqrt{\mathrm{2}}\left[\sqrt{\pi}\mathrm{FresnelC}\left(\frac{{x}}{\pi}\right)\right]_{\mathrm{0}} ^{\sqrt{\pi}} −\sqrt{\mathrm{2}}\left[\sqrt{\pi}\mathrm{FresnelC}\left(\frac{{x}}{\pi}\right)\right]_{\sqrt{\pi}} ^{\mathrm{3}} \\ $$$$\mathrm{I}\:=\:\sqrt{\mathrm{2}\pi}\left[\mathrm{2FresnelC}\left(\frac{\mathrm{1}}{\:\sqrt{\pi}}\right)−\mathrm{FresnelC}\left(\mathrm{0}\right)−\mathrm{FresnelC}\left(\mathrm{3}\right)\right] \\ $$$$\mathrm{I}\:=\:\sqrt{\mathrm{2}\pi}\left[\mathrm{2FresnelC}\left(\frac{\mathrm{1}}{\:\sqrt{\pi}}\right)−\mathrm{FresnelC}\left(\mathrm{3}\right)\right] \\ $$$$\mathrm{Note}\:: \\ $$$$\mathrm{Fresnel}\:\mathrm{Cosine}\:\mathrm{Integral} \\ $$$$\mathrm{FresnelC}\left({z}\right)\:=\:\int_{\mathrm{0}} ^{{z}} \mathrm{cos}\left(\frac{\pi{t}^{\mathrm{2}} }{\mathrm{2}}\right){dt} \\ $$
