Question Number 122120 by sina1377 last updated on 14/Nov/20

$$\underset{\mathrm{0}} {\overset{\mathrm{3}} {\int}}\frac{\mathrm{1}}{\:\sqrt{{y}}}.{e}^{{y}} {dy} \\ $$
Answered by Bird last updated on 14/Nov/20
![I =∫_0 ^3 (e^y /( (√y)))dy ⇒I =_((√y)=x) ∫_0 ^(√3) (e^x^2 /x)(2xdx) =2∫_0 ^(√3) e^x^2 dx =2∫_0 ^(√3) Σ_(n=0) ^∞ (x^(2n) /(n!))dx =2Σ_(n=0) ^∞ (1/(n!))∫_0 ^(√3) x^(2n) dx =2Σ_(n=0) ^∞ (1/(n!))[(1/(2n+1)) x^(2n+1) ]_0 ^(√3) =2 Σ_(n=0) ^∞ (1/((2n+1)n!))((√3))^(2n+1) =2(√3)Σ_(n=0) ^∞ (3^n /((2n+1)n!))](https://www.tinkutara.com/question/Q122146.png)
$${I}\:=\int_{\mathrm{0}} ^{\mathrm{3}} \:\frac{{e}^{{y}} }{\:\sqrt{{y}}}{dy}\:\:\Rightarrow{I}\:=_{\sqrt{{y}}={x}} \:\:\:\int_{\mathrm{0}} ^{\sqrt{\mathrm{3}}} \:\frac{{e}^{{x}^{\mathrm{2}} } }{{x}}\left(\mathrm{2}{xdx}\right) \\ $$$$=\mathrm{2}\int_{\mathrm{0}} ^{\sqrt{\mathrm{3}}} \:{e}^{{x}^{\mathrm{2}} } {dx}\:=\mathrm{2}\int_{\mathrm{0}} ^{\sqrt{\mathrm{3}}} \sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{{x}^{\mathrm{2}{n}} }{{n}!}{dx} \\ $$$$=\mathrm{2}\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{1}}{{n}!}\int_{\mathrm{0}} ^{\sqrt{\mathrm{3}}} \:{x}^{\mathrm{2}{n}} {dx} \\ $$$$=\mathrm{2}\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{1}}{{n}!}\left[\frac{\mathrm{1}}{\mathrm{2}{n}+\mathrm{1}}\:{x}^{\mathrm{2}{n}+\mathrm{1}} \right]_{\mathrm{0}} ^{\sqrt{\mathrm{3}}} \\ $$$$=\mathrm{2}\:\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{1}}{\left(\mathrm{2}{n}+\mathrm{1}\right){n}!}\left(\sqrt{\mathrm{3}}\right)^{\mathrm{2}{n}+\mathrm{1}} \\ $$$$=\mathrm{2}\sqrt{\mathrm{3}}\sum_{{n}=\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{3}^{{n}} }{\left(\mathrm{2}{n}+\mathrm{1}\right){n}!} \\ $$
Answered by Dwaipayan Shikari last updated on 14/Nov/20
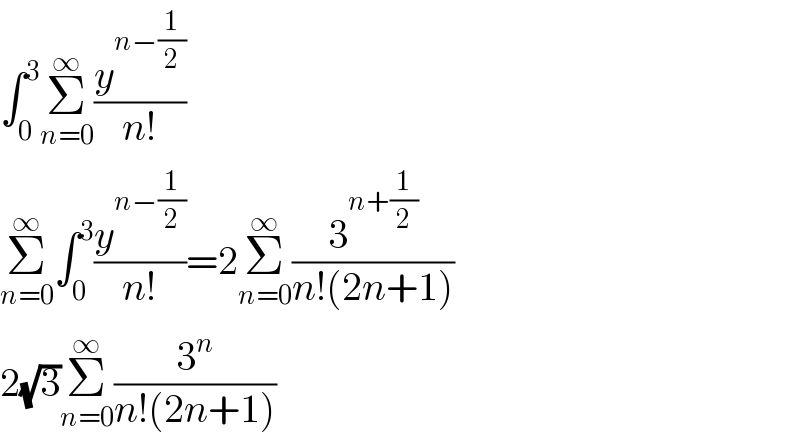
$$\int_{\mathrm{0}} ^{\mathrm{3}} \underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{{y}^{{n}−\frac{\mathrm{1}}{\mathrm{2}}} }{{n}!} \\ $$$$\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\int_{\mathrm{0}} ^{\mathrm{3}} \frac{{y}^{{n}−\frac{\mathrm{1}}{\mathrm{2}}} }{{n}!}=\mathrm{2}\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{3}^{{n}+\frac{\mathrm{1}}{\mathrm{2}}} }{{n}!\left(\mathrm{2}{n}+\mathrm{1}\right)} \\ $$$$\mathrm{2}\sqrt{\mathrm{3}}\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{3}^{{n}} }{{n}!\left(\mathrm{2}{n}+\mathrm{1}\right)} \\ $$
