Question Number 126577 by benjo_mathlover last updated on 22/Dec/20
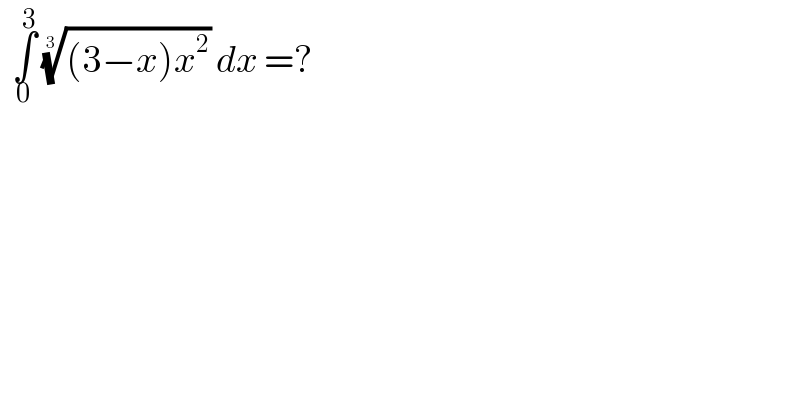
$$\:\:\underset{\mathrm{0}} {\overset{\mathrm{3}} {\int}}\:\sqrt[{\mathrm{3}}]{\left(\mathrm{3}−{x}\right){x}^{\mathrm{2}} }\:{dx}\:=?\: \\ $$
Answered by Dwaipayan Shikari last updated on 22/Dec/20
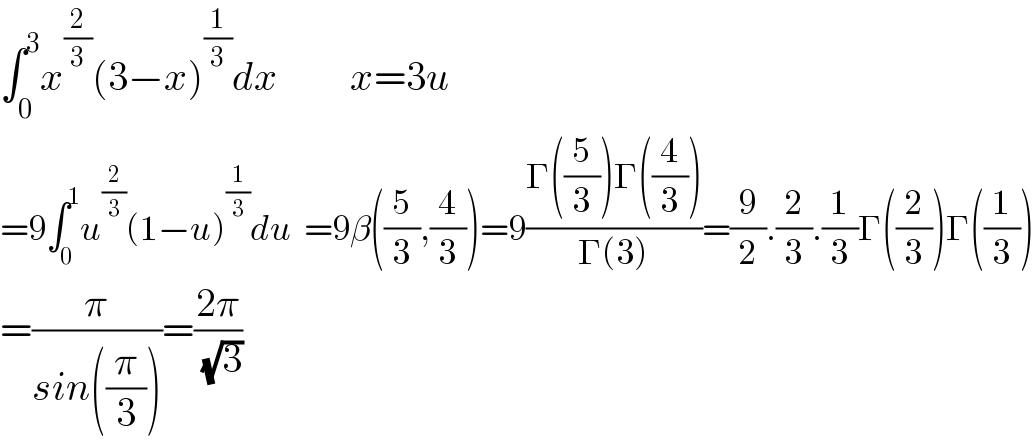
$$\int_{\mathrm{0}} ^{\mathrm{3}} {x}^{\frac{\mathrm{2}}{\mathrm{3}}} \left(\mathrm{3}−{x}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} {dx}\:\:\:\:\:\:\:\:\:{x}=\mathrm{3}{u} \\ $$$$=\mathrm{9}\int_{\mathrm{0}} ^{\mathrm{1}} {u}^{\frac{\mathrm{2}}{\mathrm{3}}} \left(\mathrm{1}−{u}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} {du}\:\:=\mathrm{9}\beta\left(\frac{\mathrm{5}}{\mathrm{3}},\frac{\mathrm{4}}{\mathrm{3}}\right)=\mathrm{9}\frac{\Gamma\left(\frac{\mathrm{5}}{\mathrm{3}}\right)\Gamma\left(\frac{\mathrm{4}}{\mathrm{3}}\right)}{\Gamma\left(\mathrm{3}\right)}=\frac{\mathrm{9}}{\mathrm{2}}.\frac{\mathrm{2}}{\mathrm{3}}.\frac{\mathrm{1}}{\mathrm{3}}\Gamma\left(\frac{\mathrm{2}}{\mathrm{3}}\right)\Gamma\left(\frac{\mathrm{1}}{\mathrm{3}}\right) \\ $$$$=\frac{\pi}{{sin}\left(\frac{\pi}{\mathrm{3}}\right)}=\frac{\mathrm{2}\pi}{\:\sqrt{\mathrm{3}}} \\ $$
Answered by liberty last updated on 22/Dec/20
![I=∫_1 ^3 x (((3/x)−1))^(1/3) dx ; [ let (3/x)−1=z^3 ] I=∫_∞ ^0 ((27z^3 )/((z^3 +1)^3 )) dz ; [by parts ] I= −(9/2)z((1/((z^3 +1)^2 )))_0 ^∞ −∫_0 ^∞ 9.(−(1/(2(z^3 +1)^2 )))dz I=(9/2)∫_0 ^( ∞) (dz/((z^3 +1)^2 )) = (9/2)∫_0 ^( ∞) (1/((1+(1/z^3 ))))((dz/z^2 )) I=∫_0 ^( ∞) ((3z)/(1+z^3 )) dz = −(1/(2πi)). lim_(R→∞) ∫_( C_R ) ((3s ln s)/(s^3 +1)) ds I=−(1/(2πi)).lim_(R→∞) ∫_C_R ((3s ln s)/(s^3 +1)) ds = −Σ_(k=0) ^2 (((2k+1)πi)/3) e^(−(2k+1)πi/3) I= ((2π)/( (√3))) = ∫_0 ^3 ((x^2 (3−x)))^(1/3) dx](https://www.tinkutara.com/question/Q126585.png)
$${I}=\underset{\mathrm{1}} {\overset{\mathrm{3}} {\int}}{x}\:\sqrt[{\mathrm{3}}]{\frac{\mathrm{3}}{{x}}−\mathrm{1}}\:{dx}\:;\:\left[\:{let}\:\frac{\mathrm{3}}{{x}}−\mathrm{1}={z}^{\mathrm{3}} \:\right] \\ $$$${I}=\underset{\infty} {\overset{\mathrm{0}} {\int}}\:\frac{\mathrm{27}{z}^{\mathrm{3}} }{\left({z}^{\mathrm{3}} +\mathrm{1}\right)^{\mathrm{3}} }\:{dz}\:;\:\left[{by}\:{parts}\:\right]\: \\ $$$${I}=\:−\frac{\mathrm{9}}{\mathrm{2}}{z}\left(\frac{\mathrm{1}}{\left({z}^{\mathrm{3}} +\mathrm{1}\right)^{\mathrm{2}} }\right)_{\mathrm{0}} ^{\infty} −\underset{\mathrm{0}} {\overset{\infty} {\int}}\:\mathrm{9}.\left(−\frac{\mathrm{1}}{\mathrm{2}\left({z}^{\mathrm{3}} +\mathrm{1}\right)^{\mathrm{2}} }\right){dz} \\ $$$${I}=\frac{\mathrm{9}}{\mathrm{2}}\int_{\mathrm{0}} ^{\:\infty} \frac{{dz}}{\left({z}^{\mathrm{3}} +\mathrm{1}\right)^{\mathrm{2}} }\:=\:\frac{\mathrm{9}}{\mathrm{2}}\int_{\mathrm{0}} ^{\:\infty} \frac{\mathrm{1}}{\left(\mathrm{1}+\frac{\mathrm{1}}{{z}^{\mathrm{3}} }\right)}\left(\frac{{dz}}{{z}^{\mathrm{2}} }\right) \\ $$$${I}=\int_{\mathrm{0}} ^{\:\infty} \frac{\mathrm{3}{z}}{\mathrm{1}+{z}^{\mathrm{3}} }\:{dz}\:=\:−\frac{\mathrm{1}}{\mathrm{2}\pi{i}}.\:\underset{{R}\rightarrow\infty} {\mathrm{lim}}\int_{\:{C}_{{R}} } \frac{\mathrm{3}{s}\:\mathrm{ln}\:{s}}{{s}^{\mathrm{3}} +\mathrm{1}}\:{ds} \\ $$$${I}=−\frac{\mathrm{1}}{\mathrm{2}\pi{i}}.\underset{{R}\rightarrow\infty} {\mathrm{lim}}\int_{{C}_{{R}} } \frac{\mathrm{3}{s}\:\mathrm{ln}\:{s}}{{s}^{\mathrm{3}} +\mathrm{1}}\:{ds}\:=\:−\underset{{k}=\mathrm{0}} {\overset{\mathrm{2}} {\sum}}\frac{\left(\mathrm{2}{k}+\mathrm{1}\right)\pi{i}}{\mathrm{3}}\:{e}^{−\left(\mathrm{2}{k}+\mathrm{1}\right)\pi{i}/\mathrm{3}} \\ $$$${I}=\:\frac{\mathrm{2}\pi}{\:\sqrt{\mathrm{3}}}\:=\:\underset{\mathrm{0}} {\overset{\mathrm{3}} {\int}}\:\sqrt[{\mathrm{3}}]{{x}^{\mathrm{2}} \left(\mathrm{3}−{x}\right)}\:{dx}\: \\ $$
