Question Number 147626 by mathdanisur last updated on 22/Jul/21
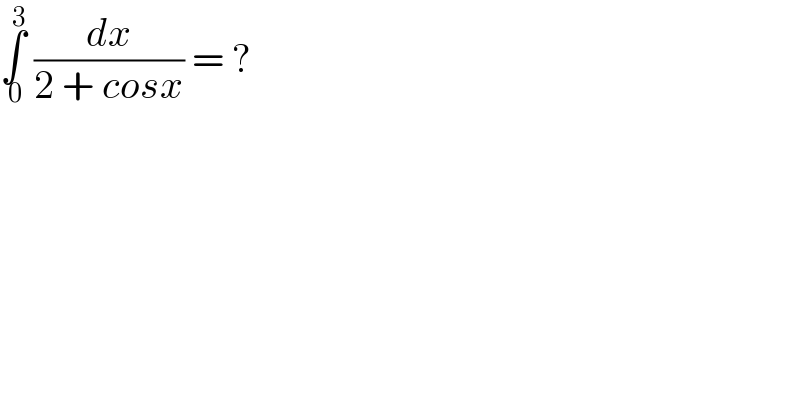
$$\underset{\:\mathrm{0}} {\overset{\:\mathrm{3}} {\int}}\:\frac{{dx}}{\mathrm{2}\:+\:{cosx}}\:=\:? \\ $$
Answered by mathmax by abdo last updated on 22/Jul/21
![I=∫_0 ^3 (dx/(2+cosx)) =_(tan((x/2))=y) ∫_0 ^(tan((3/2))) ((2dy)/((1+y^2 )(2+((1−y^2 )/(1+y^2 ))))) =2∫_0 ^(tan((3/2))) (dy/(2+2y^2 +1−y^2 ))=2∫_0 ^(tan((3/2))) (dy/(3+y^2 )) =_(y=(√3)z) 2∫_0 ^((1/( (√3)))tan((3/2))) (((√3)dz)/(3(1+z^2 )))=((2(√3))/3)[arctanz]_0 ^((1/( (√3)))tan((3/2))) ⇒ I=((2(√3))/3)arctan((1/( (√3)))tan((3/2)))](https://www.tinkutara.com/question/Q147669.png)
$$\mathrm{I}=\int_{\mathrm{0}} ^{\mathrm{3}} \:\frac{\mathrm{dx}}{\mathrm{2}+\mathrm{cosx}}\:=_{\mathrm{tan}\left(\frac{\mathrm{x}}{\mathrm{2}}\right)=\mathrm{y}} \:\:\int_{\mathrm{0}} ^{\mathrm{tan}\left(\frac{\mathrm{3}}{\mathrm{2}}\right)} \:\frac{\mathrm{2dy}}{\left(\mathrm{1}+\mathrm{y}^{\mathrm{2}} \right)\left(\mathrm{2}+\frac{\mathrm{1}−\mathrm{y}^{\mathrm{2}} }{\mathrm{1}+\mathrm{y}^{\mathrm{2}} }\right)} \\ $$$$=\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{tan}\left(\frac{\mathrm{3}}{\mathrm{2}}\right)} \:\frac{\mathrm{dy}}{\mathrm{2}+\mathrm{2y}^{\mathrm{2}} +\mathrm{1}−\mathrm{y}^{\mathrm{2}} }=\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{tan}\left(\frac{\mathrm{3}}{\mathrm{2}}\right)} \:\frac{\mathrm{dy}}{\mathrm{3}+\mathrm{y}^{\mathrm{2}} } \\ $$$$=_{\mathrm{y}=\sqrt{\mathrm{3}}\mathrm{z}} \:\:\:\:\mathrm{2}\int_{\mathrm{0}} ^{\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\mathrm{tan}\left(\frac{\mathrm{3}}{\mathrm{2}}\right)} \:\frac{\sqrt{\mathrm{3}}\mathrm{dz}}{\mathrm{3}\left(\mathrm{1}+\mathrm{z}^{\mathrm{2}} \right)}=\frac{\mathrm{2}\sqrt{\mathrm{3}}}{\mathrm{3}}\left[\mathrm{arctanz}\right]_{\mathrm{0}} ^{\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\mathrm{tan}\left(\frac{\mathrm{3}}{\mathrm{2}}\right)} \:\Rightarrow \\ $$$$\mathrm{I}=\frac{\mathrm{2}\sqrt{\mathrm{3}}}{\mathrm{3}}\mathrm{arctan}\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\mathrm{tan}\left(\frac{\mathrm{3}}{\mathrm{2}}\right)\right) \\ $$
Commented by mathdanisur last updated on 22/Jul/21

$${thank}\:{youSir} \\ $$
Answered by gsk2684 last updated on 22/Jul/21
![∫_(x=0) ^3 (1/(2+(((1−tan^2 (x/2))/(1+tan^2 (x/2))))))dx=∫_0 ^3 ((sec^2 (x/2))/(3+tan^2 (x/2)))dx put tan (x/2)=t ⇒ (1/2) sec^2 (x/2) dx=dt if x=0 then t=0 if x=3 then t=tan (3/2) =∫_(t=0) ^(tan (3/2)) (2/( ((√3))^2 +t^2 )) dt=2 [(1/( (√3)))tan^(−1) (t/( (√3)))]_0 ^(tan (3/2)) =(2/( (√3)))[tan^(−1) (((tan (3/2))/( (√3))))−tan^(−1) 0] =(2/( (√3)))tan^(−1) (((tan (3/2))/( (√3))))](https://www.tinkutara.com/question/Q147631.png)
$$\underset{{x}=\mathrm{0}} {\overset{\mathrm{3}} {\int}}\frac{\mathrm{1}}{\mathrm{2}+\left(\frac{\mathrm{1}−\mathrm{tan}\:^{\mathrm{2}} \frac{{x}}{\mathrm{2}}}{\mathrm{1}+\mathrm{tan}\:^{\mathrm{2}} \frac{{x}}{\mathrm{2}}}\right)}{dx}=\underset{\mathrm{0}} {\overset{\mathrm{3}} {\int}}\frac{\mathrm{sec}\:^{\mathrm{2}} \frac{{x}}{\mathrm{2}}}{\mathrm{3}+\mathrm{tan}\:^{\mathrm{2}} \frac{{x}}{\mathrm{2}}}{dx} \\ $$$${put}\:\mathrm{tan}\:\frac{{x}}{\mathrm{2}}={t}\:\Rightarrow\:\frac{\mathrm{1}}{\mathrm{2}}\:\mathrm{sec}\:^{\mathrm{2}} \frac{{x}}{\mathrm{2}}\:{dx}={dt} \\ $$$${if}\:{x}=\mathrm{0}\:{then}\:{t}=\mathrm{0} \\ $$$${if}\:{x}=\mathrm{3}\:{then}\:{t}=\mathrm{tan}\:\frac{\mathrm{3}}{\mathrm{2}} \\ $$$$=\underset{{t}=\mathrm{0}} {\overset{\mathrm{tan}\:\frac{\mathrm{3}}{\mathrm{2}}} {\int}}\frac{\mathrm{2}}{\:\left(\sqrt{\mathrm{3}}\right)^{\mathrm{2}} +{t}^{\mathrm{2}} }\:\:{dt}=\mathrm{2}\:\left[\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\mathrm{tan}^{−\mathrm{1}} \frac{{t}}{\:\sqrt{\mathrm{3}}}\right]_{\mathrm{0}} ^{\mathrm{tan}\:\frac{\mathrm{3}}{\mathrm{2}}} \\ $$$$=\frac{\mathrm{2}}{\:\sqrt{\mathrm{3}}}\left[\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{tan}\:\frac{\mathrm{3}}{\mathrm{2}}}{\:\sqrt{\mathrm{3}}}\right)−\mathrm{tan}^{−\mathrm{1}} \mathrm{0}\right] \\ $$$$=\frac{\mathrm{2}}{\:\sqrt{\mathrm{3}}}\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{tan}\:\frac{\mathrm{3}}{\mathrm{2}}}{\:\sqrt{\mathrm{3}}}\right) \\ $$
Commented by mathdanisur last updated on 22/Jul/21

$${thank}\:{you}\:{Sir} \\ $$
