Question Number 146859 by mathdanisur last updated on 16/Jul/21
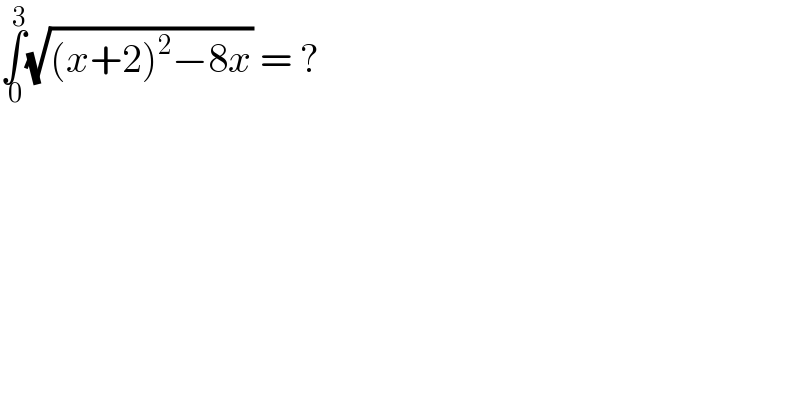
$$\underset{\:\mathrm{0}} {\overset{\mathrm{3}} {\int}}\sqrt{\left({x}+\mathrm{2}\right)^{\mathrm{2}} −\mathrm{8}{x}}\:=\:? \\ $$
Answered by mathmax by abdo last updated on 16/Jul/21
![I=∫_0 ^3 (√((x+2)^2 −8x))dx ⇒I=∫_0 ^3 (√(x^2 +4x+4−8x))dx =∫_0 ^3 (√((x−2)^2 ))dx =∫_0 ^3 ∣x−2∣dx=∫_0 ^2 ∣x−2∣dx+∫_2 ^3 ∣x−2∣dx =∫_0 ^2 (2−x)dx +∫_2 ^3 (x−2)dx =[2x−(x^2 /2)]_0 ^2 +[(x^2 /2)−2x]_2 ^3 =4−2 +(9/2)−6−2+4 =−2+(9/2)=(5/2)](https://www.tinkutara.com/question/Q146918.png)
$$\mathrm{I}=\int_{\mathrm{0}} ^{\mathrm{3}} \sqrt{\left(\mathrm{x}+\mathrm{2}\right)^{\mathrm{2}} −\mathrm{8x}}\mathrm{dx}\:\Rightarrow\mathrm{I}=\int_{\mathrm{0}} ^{\mathrm{3}} \sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{4x}+\mathrm{4}−\mathrm{8x}}\mathrm{dx} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{3}} \sqrt{\left(\mathrm{x}−\mathrm{2}\right)^{\mathrm{2}} }\mathrm{dx}\:=\int_{\mathrm{0}} ^{\mathrm{3}} \mid\mathrm{x}−\mathrm{2}\mid\mathrm{dx}=\int_{\mathrm{0}} ^{\mathrm{2}} \:\mid\mathrm{x}−\mathrm{2}\mid\mathrm{dx}+\int_{\mathrm{2}} ^{\mathrm{3}} \mid\mathrm{x}−\mathrm{2}\mid\mathrm{dx} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{2}} \left(\mathrm{2}−\mathrm{x}\right)\mathrm{dx}\:+\int_{\mathrm{2}} ^{\mathrm{3}} \left(\mathrm{x}−\mathrm{2}\right)\mathrm{dx}\:=\left[\mathrm{2x}−\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}}\right]_{\mathrm{0}} ^{\mathrm{2}} \:+\left[\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}}−\mathrm{2x}\right]_{\mathrm{2}} ^{\mathrm{3}} \\ $$$$=\mathrm{4}−\mathrm{2}\:+\frac{\mathrm{9}}{\mathrm{2}}−\mathrm{6}−\mathrm{2}+\mathrm{4}\:=−\mathrm{2}+\frac{\mathrm{9}}{\mathrm{2}}=\frac{\mathrm{5}}{\mathrm{2}} \\ $$
Commented by mathdanisur last updated on 16/Jul/21

$${thank}\:{you}\:{Ser} \\ $$
