Question Number 128834 by bounhome last updated on 10/Jan/21
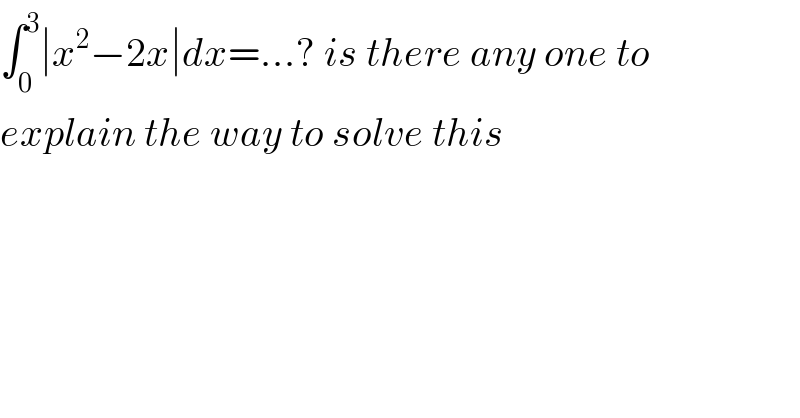
$$\int_{\mathrm{0}} ^{\mathrm{3}} \mid{x}^{\mathrm{2}} −\mathrm{2}{x}\mid{dx}=…?\:{is}\:{there}\:{any}\:{one}\:{to}\: \\ $$$${explain}\:{the}\:{way}\:{to}\:{solve}\:{this}\: \\ $$
Answered by bobhans last updated on 10/Jan/21
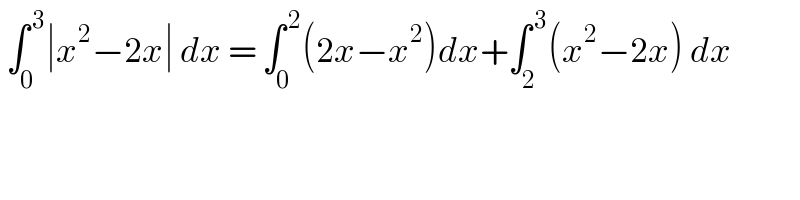
$$\:\int_{\mathrm{0}} ^{\:\mathrm{3}} \mid{x}^{\mathrm{2}} −\mathrm{2}{x}\mid\:{dx}\:=\:\int_{\mathrm{0}} ^{\:\mathrm{2}} \left(\mathrm{2}{x}−{x}^{\mathrm{2}} \right){dx}+\int_{\mathrm{2}} ^{\:\mathrm{3}} \left({x}^{\mathrm{2}} −\mathrm{2}{x}\right)\:{dx} \\ $$
Answered by mathmax by abdo last updated on 10/Jan/21
![∫_0 ^3 ∣x^2 −2x∣dx =∫_0 ^3 x∣x−2∣dx =∫_0 ^2 x(2−x)dx +∫_2 ^3 x(x−2)dx =∫_0 ^2 (2x−x^2 )dx+∫_2 ^3 (x^2 −2x)dx =[x^2 −(x^3 /3)]_0 ^2 +[(x^3 /3)−x^2 ]_2 ^3 =2^2 −(2^3 /3) +((3^3 /3)−3^2 −(2^3 /3) +2^2 )=4−(8/3) −(8/3) +4 =8−((16)/3)=((24−16)/3) =(8/3)](https://www.tinkutara.com/question/Q128840.png)
$$\int_{\mathrm{0}} ^{\mathrm{3}} \mid\mathrm{x}^{\mathrm{2}} −\mathrm{2x}\mid\mathrm{dx}\:=\int_{\mathrm{0}} ^{\mathrm{3}} \mathrm{x}\mid\mathrm{x}−\mathrm{2}\mid\mathrm{dx}\:=\int_{\mathrm{0}} ^{\mathrm{2}} \mathrm{x}\left(\mathrm{2}−\mathrm{x}\right)\mathrm{dx}\:+\int_{\mathrm{2}} ^{\mathrm{3}} \mathrm{x}\left(\mathrm{x}−\mathrm{2}\right)\mathrm{dx} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{2}} \left(\mathrm{2x}−\mathrm{x}^{\mathrm{2}} \right)\mathrm{dx}+\int_{\mathrm{2}} ^{\mathrm{3}} \left(\mathrm{x}^{\mathrm{2}} −\mathrm{2x}\right)\mathrm{dx}\:=\left[\mathrm{x}^{\mathrm{2}} −\frac{\mathrm{x}^{\mathrm{3}} }{\mathrm{3}}\right]_{\mathrm{0}} ^{\mathrm{2}} \:+\left[\frac{\mathrm{x}^{\mathrm{3}} }{\mathrm{3}}−\mathrm{x}^{\mathrm{2}} \right]_{\mathrm{2}} ^{\mathrm{3}} \\ $$$$=\mathrm{2}^{\mathrm{2}} −\frac{\mathrm{2}^{\mathrm{3}} }{\mathrm{3}}\:+\left(\frac{\mathrm{3}^{\mathrm{3}} }{\mathrm{3}}−\mathrm{3}^{\mathrm{2}} \:−\frac{\mathrm{2}^{\mathrm{3}} }{\mathrm{3}}\:+\mathrm{2}^{\mathrm{2}} \right)=\mathrm{4}−\frac{\mathrm{8}}{\mathrm{3}}\:−\frac{\mathrm{8}}{\mathrm{3}}\:+\mathrm{4}\:=\mathrm{8}−\frac{\mathrm{16}}{\mathrm{3}}=\frac{\mathrm{24}−\mathrm{16}}{\mathrm{3}} \\ $$$$=\frac{\mathrm{8}}{\mathrm{3}} \\ $$
