Question Number 64984 by naka3546 last updated on 23/Jul/19

$$\underset{\mathrm{0}} {\int}\:\overset{\mathrm{3}} {\:}\:{x}\:\mid{x}^{\mathrm{2}} \:−\:{x}\:−\:\mathrm{2}\mid\:{dx}\:\:=\:\:? \\ $$
Commented by kaivan.ahmadi last updated on 23/Jul/19
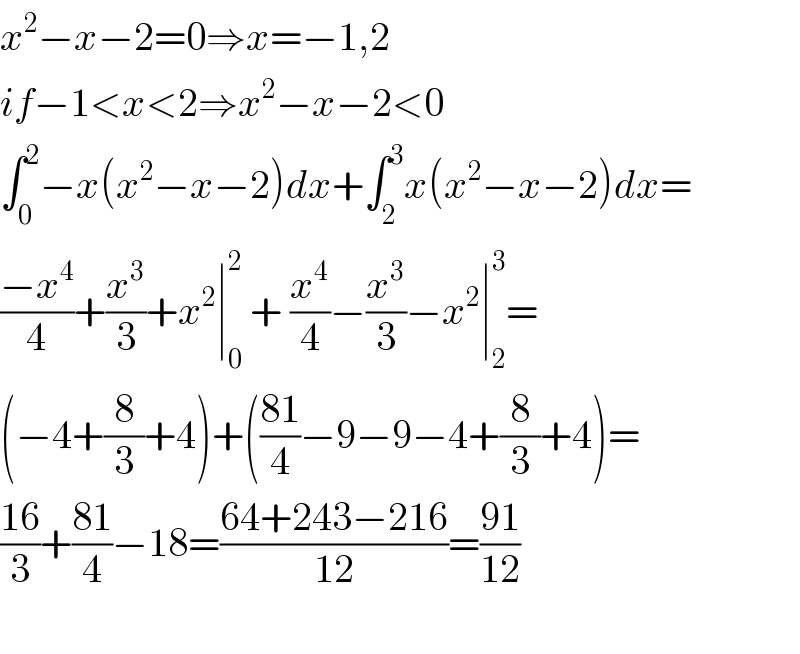
$${x}^{\mathrm{2}} −{x}−\mathrm{2}=\mathrm{0}\Rightarrow{x}=−\mathrm{1},\mathrm{2} \\ $$$${if}−\mathrm{1}<{x}<\mathrm{2}\Rightarrow{x}^{\mathrm{2}} −{x}−\mathrm{2}<\mathrm{0} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{2}} −{x}\left({x}^{\mathrm{2}} −{x}−\mathrm{2}\right){dx}+\int_{\mathrm{2}} ^{\mathrm{3}} {x}\left({x}^{\mathrm{2}} −{x}−\mathrm{2}\right){dx}= \\ $$$$\frac{−{x}^{\mathrm{4}} }{\mathrm{4}}+\frac{{x}^{\mathrm{3}} }{\mathrm{3}}+{x}^{\mathrm{2}} \mid_{\mathrm{0}} ^{\mathrm{2}} \:+\:\frac{{x}^{\mathrm{4}} }{\mathrm{4}}−\frac{{x}^{\mathrm{3}} }{\mathrm{3}}−{x}^{\mathrm{2}} \mid_{\mathrm{2}} ^{\mathrm{3}} = \\ $$$$\left(−\mathrm{4}+\frac{\mathrm{8}}{\mathrm{3}}+\mathrm{4}\right)+\left(\frac{\mathrm{81}}{\mathrm{4}}−\mathrm{9}−\mathrm{9}−\mathrm{4}+\frac{\mathrm{8}}{\mathrm{3}}+\mathrm{4}\right)= \\ $$$$\frac{\mathrm{16}}{\mathrm{3}}+\frac{\mathrm{81}}{\mathrm{4}}−\mathrm{18}=\frac{\mathrm{64}+\mathrm{243}−\mathrm{216}}{\mathrm{12}}=\frac{\mathrm{91}}{\mathrm{12}} \\ $$$$ \\ $$
Commented by mathmax by abdo last updated on 24/Jul/19
![x^2 −x−2 =0→Δ =1+8 =9 ⇒x_1 =((1+3)/2) =2 and x_2 =((1−3)/2) =−1 ⇒ ∫_0 ^3 x∣x^2 −x−2∣dx =∫_0 ^3 x∣x+1∣∣x−2∣dx =∫_0 ^3 (x^2 +x)∣x−2∣dx =∫_0 ^2 (x^2 +x)(2−x)dx +∫_2 ^3 (x^2 +x)(x−2)dx =∫_0 ^2 (2x^2 −x^3 +2x−x^2 )dx +∫_2 ^3 (x^3 −2x^2 +x^2 −2x)dx =∫_0 ^2 (−x^3 +x^2 +2x)dx +∫_2 ^3 (x^3 −x^2 −2x)dx =[−(x^4 /4) +(x^3 /3) +x^2 ]_0 ^2 +[(x^4 /4) −(x^3 /3) −x^2 ]_2 ^3 ={−4 +(8/3) +4)+(((81)/4) −((27)/3) −9−4+(8/3) +4) =(8/3) +((81)/4) −18 +(8/3) =((16)/3) +((81)/4) −18 =...](https://www.tinkutara.com/question/Q65002.png)
$${x}^{\mathrm{2}} −{x}−\mathrm{2}\:=\mathrm{0}\rightarrow\Delta\:=\mathrm{1}+\mathrm{8}\:=\mathrm{9}\:\Rightarrow{x}_{\mathrm{1}} =\frac{\mathrm{1}+\mathrm{3}}{\mathrm{2}}\:=\mathrm{2}\:{and}\:{x}_{\mathrm{2}} =\frac{\mathrm{1}−\mathrm{3}}{\mathrm{2}}\:=−\mathrm{1}\:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\mathrm{3}} {x}\mid{x}^{\mathrm{2}} −{x}−\mathrm{2}\mid{dx}\:=\int_{\mathrm{0}} ^{\mathrm{3}} {x}\mid{x}+\mathrm{1}\mid\mid{x}−\mathrm{2}\mid{dx}\:=\int_{\mathrm{0}} ^{\mathrm{3}} \left({x}^{\mathrm{2}} +{x}\right)\mid{x}−\mathrm{2}\mid{dx} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{2}} \left({x}^{\mathrm{2}} +{x}\right)\left(\mathrm{2}−{x}\right){dx}\:+\int_{\mathrm{2}} ^{\mathrm{3}} \left({x}^{\mathrm{2}} \:+{x}\right)\left({x}−\mathrm{2}\right){dx} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{2}} \left(\mathrm{2}{x}^{\mathrm{2}} −{x}^{\mathrm{3}} \:+\mathrm{2}{x}−{x}^{\mathrm{2}} \right){dx}\:+\int_{\mathrm{2}} ^{\mathrm{3}} \left({x}^{\mathrm{3}} −\mathrm{2}{x}^{\mathrm{2}} +{x}^{\mathrm{2}} −\mathrm{2}{x}\right){dx} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{2}} \left(−{x}^{\mathrm{3}} \:+{x}^{\mathrm{2}} +\mathrm{2}{x}\right){dx}\:+\int_{\mathrm{2}} ^{\mathrm{3}} \left({x}^{\mathrm{3}} −{x}^{\mathrm{2}} −\mathrm{2}{x}\right){dx} \\ $$$$=\left[−\frac{{x}^{\mathrm{4}} }{\mathrm{4}}\:+\frac{{x}^{\mathrm{3}} }{\mathrm{3}}\:+{x}^{\mathrm{2}} \right]_{\mathrm{0}} ^{\mathrm{2}} \:\:+\left[\frac{{x}^{\mathrm{4}} }{\mathrm{4}}\:−\frac{{x}^{\mathrm{3}} }{\mathrm{3}}\:−{x}^{\mathrm{2}} \right]_{\mathrm{2}} ^{\mathrm{3}} \\ $$$$=\left\{−\mathrm{4}\:+\frac{\mathrm{8}}{\mathrm{3}}\:+\mathrm{4}\right)+\left(\frac{\mathrm{81}}{\mathrm{4}}\:−\frac{\mathrm{27}}{\mathrm{3}}\:−\mathrm{9}−\mathrm{4}+\frac{\mathrm{8}}{\mathrm{3}}\:+\mathrm{4}\right) \\ $$$$=\frac{\mathrm{8}}{\mathrm{3}}\:+\frac{\mathrm{81}}{\mathrm{4}}\:−\mathrm{18}\:+\frac{\mathrm{8}}{\mathrm{3}}\:=\frac{\mathrm{16}}{\mathrm{3}}\:+\frac{\mathrm{81}}{\mathrm{4}}\:−\mathrm{18}\:=… \\ $$
Answered by ajfour last updated on 23/Jul/19
![∫_0 ^( 3) x(x−2)(x+1)dx =−∫_0 ^( 2) (x^3 −x^2 −2x)dx+∫_2 ^( 3) (x^3 −x^2 −2x)dx =−[(x^4 /4)−(x^3 /3)−x^2 ]_0 ^2 +[(x^4 /4)−(x^3 /3)−x^2 ]_2 ^3 =−2(4−(8/3)−4)+(((81)/4)−9−9) =((16)/3)+(9/4) =((91)/(12))=7(7/(12)) .](https://www.tinkutara.com/question/Q64989.png)
$$\int_{\mathrm{0}} ^{\:\mathrm{3}} {x}\left({x}−\mathrm{2}\right)\left({x}+\mathrm{1}\right){dx} \\ $$$$=−\int_{\mathrm{0}} ^{\:\mathrm{2}} \left({x}^{\mathrm{3}} −{x}^{\mathrm{2}} −\mathrm{2}{x}\right){dx}+\int_{\mathrm{2}} ^{\:\mathrm{3}} \left({x}^{\mathrm{3}} −{x}^{\mathrm{2}} −\mathrm{2}{x}\right){dx} \\ $$$$=−\left[\frac{{x}^{\mathrm{4}} }{\mathrm{4}}−\frac{{x}^{\mathrm{3}} }{\mathrm{3}}−{x}^{\mathrm{2}} \right]_{\mathrm{0}} ^{\mathrm{2}} +\left[\frac{{x}^{\mathrm{4}} }{\mathrm{4}}−\frac{{x}^{\mathrm{3}} }{\mathrm{3}}−{x}^{\mathrm{2}} \right]_{\mathrm{2}} ^{\mathrm{3}} \\ $$$$=−\mathrm{2}\left(\mathrm{4}−\frac{\mathrm{8}}{\mathrm{3}}−\mathrm{4}\right)+\left(\frac{\mathrm{81}}{\mathrm{4}}−\mathrm{9}−\mathrm{9}\right) \\ $$$$=\frac{\mathrm{16}}{\mathrm{3}}+\frac{\mathrm{9}}{\mathrm{4}}\:=\frac{\mathrm{91}}{\mathrm{12}}=\mathrm{7}\frac{\mathrm{7}}{\mathrm{12}}\:. \\ $$
