0-3pi-1-sin-4-3-cos-2-3-d-

Question Number 89511 by M±th+et£s last updated on 17/Apr/20

∫_0 ^(3π) (√(1+sin^4 (θ/3) cos^2 (θ/3))) dθ

$$\int_{\mathrm{0}} ^{\mathrm{3}\pi} \sqrt{\mathrm{1}+{sin}^{\mathrm{4}} \frac{\theta}{\mathrm{3}}\:{cos}^{\mathrm{2}} \frac{\theta}{\mathrm{3}}}\:{d}\theta \\ $$

Commented by mr W last updated on 17/Apr/20

please go to Q89482 and report that you also have this problem since a long time.

$${please}\:{go}\:{to}\:{Q}\mathrm{89482}\:{and}\:{report}\:{that} \\ $$$${you}\:{also}\:{have}\:{this}\:{problem}\:{since}\:{a} \\ $$$${long}\:{time}. \\ $$

Commented by mr W last updated on 17/Apr/20

$${did}\:{you}\:{report}\:{once}\:{that}\:{you}\:{can}\:{not} \\ $$$${edit}\:{your}\:{existing}\:{posts}?\:{now}\:{i}\:{have} \\ $$$${the}\:{same}\:{problem}. \\ $$

Commented by M±th+et£s last updated on 17/Apr/20

$${i}\:{have}\:{this}\:{problem}\:{from}\:{a}\:{long}\:{time} \\ $$$${and}\:{till}\:{now}\:{i}\:{cant}\:{delete}\:{or}\:{edit}\:{my}\:{posts} \\ $$

Commented by M±th+et£s last updated on 17/Apr/20

$${ok}\:{sir}\: \\ $$

Commented by abdomathmax last updated on 17/Apr/20

$${sir}\:{mrw}\:{if}\:{you}\:{have}\:{a}\:{problem}\:{with}\:{your} \\ $$$${phone}\:{change}\:{it}\:{with}\:{another}\:{or}\:{work}\:{with} \\ $$$${a}\:{tablet}\:{like}\:{me}….{its}\:{eazy}…. \\ $$

Commented by mr W last updated on 18/Apr/20

$${thanks}\:{for}\:{the}\:{hint}\:{sir}!\:{i}'{ll}\:{consider}. \\ $$$${but}\:{now}\:{the}\:{problem}\:{is}\:{solved}\:{by}\:{the} \\ $$$${developer}. \\ $$

Answered by ajfour last updated on 19/Apr/20

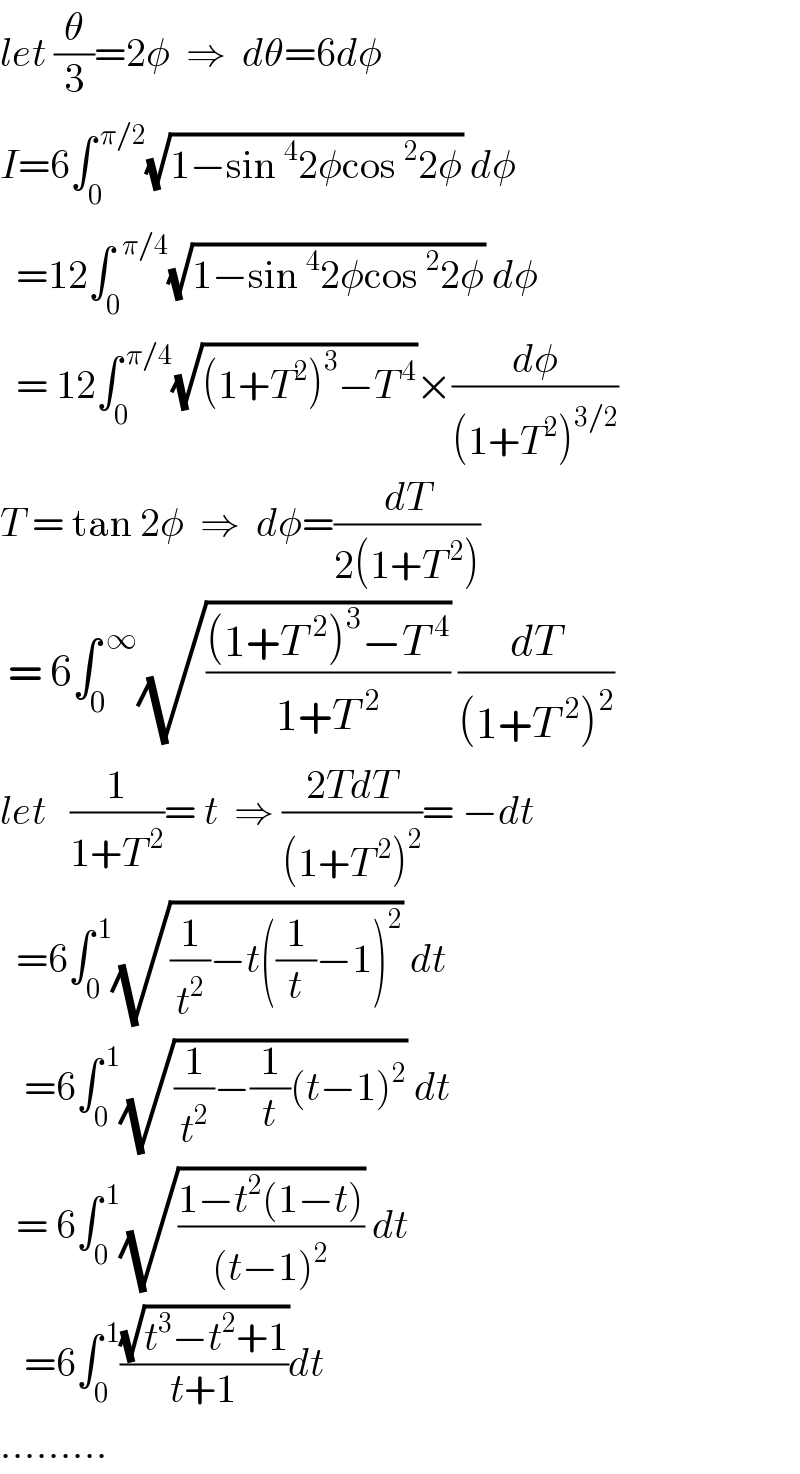
let (θ/3)=2φ ⇒ dθ=6dφ I=6∫_0 ^( π/2) (√(1−sin^4 2φcos^2 2φ)) dφ =12∫_0 ^( π/4) (√(1−sin^4 2φcos^2 2φ)) dφ = 12∫_0 ^( π/4) (√((1+T^2 )^3 −T^( 4) ))×(dφ/((1+T^2 )^(3/2) )) T = tan 2φ ⇒ dφ=(dT/(2(1+T^( 2) ))) = 6∫_0 ^( ∞) (√(((1+T^( 2) )^3 −T^( 4) )/(1+T^( 2) ))) (dT/((1+T^( 2) )^2 )) let (1/(1+T^( 2) ))= t ⇒ ((2TdT)/((1+T^( 2) )^2 ))= −dt =6∫_0 ^( 1) (√((1/t^2 )−t((1/t)−1)^2 )) dt =6∫_0 ^( 1) (√((1/t^2 )−(1/t)(t−1)^2 )) dt = 6∫_0 ^( 1) (√((1−t^2 (1−t))/((t−1)^2 ))) dt =6∫_0 ^( 1) ((√(t^3 −t^2 +1))/(t+1))dt .........

$${let}\:\frac{\theta}{\mathrm{3}}=\mathrm{2}\phi\:\:\Rightarrow\:\:{d}\theta=\mathrm{6}{d}\phi \\ $$$${I}=\mathrm{6}\int_{\mathrm{0}} ^{\:\pi/\mathrm{2}} \sqrt{\mathrm{1}−\mathrm{sin}\:^{\mathrm{4}} \mathrm{2}\phi\mathrm{cos}\:^{\mathrm{2}} \mathrm{2}\phi}\:{d}\phi \\ $$$$\:\:=\mathrm{12}\int_{\mathrm{0}} ^{\:\:\pi/\mathrm{4}} \sqrt{\mathrm{1}−\mathrm{sin}\:^{\mathrm{4}} \mathrm{2}\phi\mathrm{cos}\:^{\mathrm{2}} \mathrm{2}\phi}\:{d}\phi \\ $$$$\:\:=\:\mathrm{12}\int_{\mathrm{0}} ^{\:\pi/\mathrm{4}} \sqrt{\left(\mathrm{1}+{T}^{\mathrm{2}} \right)^{\mathrm{3}} −{T}^{\:\mathrm{4}} }×\frac{{d}\phi}{\left(\mathrm{1}+{T}^{\mathrm{2}} \right)^{\mathrm{3}/\mathrm{2}} } \\ $$$${T}\:=\:\mathrm{tan}\:\mathrm{2}\phi\:\:\Rightarrow\:\:{d}\phi=\frac{{dT}}{\mathrm{2}\left(\mathrm{1}+{T}^{\:\mathrm{2}} \right)} \\ $$$$\:=\:\mathrm{6}\int_{\mathrm{0}} ^{\:\infty} \sqrt{\frac{\left(\mathrm{1}+{T}^{\:\mathrm{2}} \right)^{\mathrm{3}} −{T}^{\:\mathrm{4}} }{\mathrm{1}+{T}^{\:\mathrm{2}} }}\:\frac{{dT}}{\left(\mathrm{1}+{T}^{\:\mathrm{2}} \right)^{\mathrm{2}} } \\ $$$${let}\:\:\:\frac{\mathrm{1}}{\mathrm{1}+{T}^{\:\mathrm{2}} }=\:{t}\:\:\Rightarrow\:\frac{\mathrm{2}{TdT}}{\left(\mathrm{1}+{T}^{\:\mathrm{2}} \right)^{\mathrm{2}} }=\:−{dt} \\ $$$$\:\:=\mathrm{6}\int_{\mathrm{0}} ^{\:\mathrm{1}} \sqrt{\frac{\mathrm{1}}{{t}^{\mathrm{2}} }−{t}\left(\frac{\mathrm{1}}{{t}}−\mathrm{1}\right)^{\mathrm{2}} }\:{dt} \\ $$$$\:\:\:=\mathrm{6}\int_{\mathrm{0}} ^{\:\mathrm{1}} \sqrt{\frac{\mathrm{1}}{{t}^{\mathrm{2}} }−\frac{\mathrm{1}}{{t}}\left({t}−\mathrm{1}\right)^{\mathrm{2}} }\:{dt}\:\: \\ $$$$\:\:=\:\mathrm{6}\int_{\mathrm{0}} ^{\:\mathrm{1}} \sqrt{\frac{\mathrm{1}−{t}^{\mathrm{2}} \left(\mathrm{1}−{t}\right)}{\left({t}−\mathrm{1}\right)^{\mathrm{2}} }}\:{dt} \\ $$$$\:\:\:=\mathrm{6}\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{\sqrt{{t}^{\mathrm{3}} −{t}^{\mathrm{2}} +\mathrm{1}}}{{t}+\mathrm{1}}{dt} \\ $$$$……… \\ $$

Facebook Tweet Pin

0-3pi-1-sin-4-3-cos-2-3-d-

Leave a Reply Cancel reply