Question Number 167554 by cortano1 last updated on 19/Mar/22
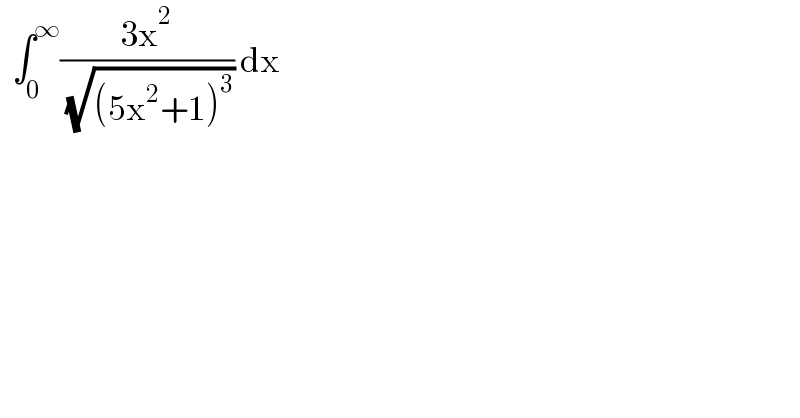
$$\:\:\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{3x}^{\mathrm{2}} }{\:\sqrt{\left(\mathrm{5x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{3}} }}\:\mathrm{dx} \\ $$$$ \\ $$
Answered by MJS_new last updated on 19/Mar/22
![∫((3x^2 )/((5x^2 +1)^(3/2) ))dx= [t=(√5)x+(√(5x^2 +1)) → dx=((√(5x^2 +1))/( (√5)t))] =((3(√5))/(25))∫(((t^2 −1)^2 )/(t(t^2 +1)^2 ))dt= =((3(√5))/(25))∫(dt/t)−((12(√5))/(25))∫(t/((t^2 +1)^2 ))dt= =((3(√5))/(25))ln t +((6(√5))/(25(t^2 +1)))= =((3(√5))/(25))ln ((√5)x+(√(5x^2 +1))) −((3x)/(5(√(5x^2 +1))))+C](https://www.tinkutara.com/question/Q167556.png)
$$\int\frac{\mathrm{3}{x}^{\mathrm{2}} }{\left(\mathrm{5}{x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{3}/\mathrm{2}} }{dx}= \\ $$$$\:\:\:\:\:\left[{t}=\sqrt{\mathrm{5}}{x}+\sqrt{\mathrm{5}{x}^{\mathrm{2}} +\mathrm{1}}\:\rightarrow\:{dx}=\frac{\sqrt{\mathrm{5}{x}^{\mathrm{2}} +\mathrm{1}}}{\:\sqrt{\mathrm{5}}{t}}\right] \\ $$$$=\frac{\mathrm{3}\sqrt{\mathrm{5}}}{\mathrm{25}}\int\frac{\left({t}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} }{{t}\left({t}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }{dt}= \\ $$$$=\frac{\mathrm{3}\sqrt{\mathrm{5}}}{\mathrm{25}}\int\frac{{dt}}{{t}}−\frac{\mathrm{12}\sqrt{\mathrm{5}}}{\mathrm{25}}\int\frac{{t}}{\left({t}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }{dt}= \\ $$$$=\frac{\mathrm{3}\sqrt{\mathrm{5}}}{\mathrm{25}}\mathrm{ln}\:{t}\:+\frac{\mathrm{6}\sqrt{\mathrm{5}}}{\mathrm{25}\left({t}^{\mathrm{2}} +\mathrm{1}\right)}= \\ $$$$=\frac{\mathrm{3}\sqrt{\mathrm{5}}}{\mathrm{25}}\mathrm{ln}\:\left(\sqrt{\mathrm{5}}{x}+\sqrt{\mathrm{5}{x}^{\mathrm{2}} +\mathrm{1}}\right)\:−\frac{\mathrm{3}{x}}{\mathrm{5}\sqrt{\mathrm{5}{x}^{\mathrm{2}} +\mathrm{1}}}+{C} \\ $$
Commented by cortano1 last updated on 19/Mar/22
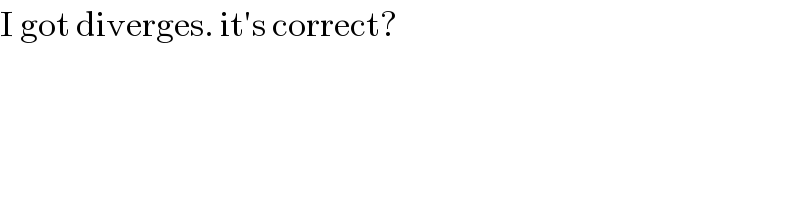
$$\mathrm{I}\:\mathrm{got}\:\mathrm{diverges}.\:\mathrm{it}'\mathrm{s}\:\mathrm{correct}? \\ $$
Commented by MJS_new last updated on 19/Mar/22

$$\mathrm{yes} \\ $$
Commented by cortano1 last updated on 19/Mar/22

$$\mathrm{thanks}\:\mathrm{sir} \\ $$
Answered by greogoury55 last updated on 19/Mar/22
![set x(√5) = tan y I= ∫_0 ^(π/2) ((3(((tan^2 y)/5)))/( ((√(sec^2 y)))^3 ))(((sec^2 y)/( (√5))))dy I= (3/(5(√5))) ∫_0 ^(π/2) ((tan^2 y)/(sec y)) dy I= (3/(5(√5))) ∫_0 ^( (π/2)) ((1−cos^2 y)/(cos y)) dy I= (3/(5(√5))) [ ln ∣sec y+tan y∣−sin y ]_0 ^(π/2) Diverges](https://www.tinkutara.com/question/Q167561.png)
$$\:{set}\:{x}\sqrt{\mathrm{5}}\:=\:\mathrm{tan}\:{y}\: \\ $$$$\:{I}=\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\mathrm{3}\left(\frac{\mathrm{tan}\:^{\mathrm{2}} {y}}{\mathrm{5}}\right)}{\:\left(\sqrt{\mathrm{sec}\:^{\mathrm{2}} {y}}\right)^{\mathrm{3}} }\left(\frac{\mathrm{sec}\:^{\mathrm{2}} {y}}{\:\sqrt{\mathrm{5}}}\right){dy}\: \\ $$$$\:{I}=\:\frac{\mathrm{3}}{\mathrm{5}\sqrt{\mathrm{5}}}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\mathrm{tan}\:^{\mathrm{2}} {y}}{\mathrm{sec}\:{y}}\:{dy}\: \\ $$$$\:{I}=\:\frac{\mathrm{3}}{\mathrm{5}\sqrt{\mathrm{5}}}\:\int_{\mathrm{0}} ^{\:\frac{\pi}{\mathrm{2}}} \frac{\mathrm{1}−\mathrm{cos}\:^{\mathrm{2}} {y}}{\mathrm{cos}\:{y}}\:{dy} \\ $$$$\:{I}=\:\frac{\mathrm{3}}{\mathrm{5}\sqrt{\mathrm{5}}}\:\left[\:\mathrm{ln}\:\mid\mathrm{sec}\:{y}+\mathrm{tan}\:{y}\mid−\mathrm{sin}\:{y}\:\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \\ $$$$\:{Diverges} \\ $$
Answered by Mathspace last updated on 20/Mar/22
![(√5)x=tant ⇒I=(1/( (√5)))∫_0 ^(π/2) ((3(((tant)/( (√5))))^2 )/((1+tan^2 )^(3/2) ))(1+tan^2 t)dt =(3/(5(√5)))∫_0 ^(π/2) ((tan^2 t)/( (√(1+tan^2 ))))dt =(3/(5(√5)))∫_0 ^(π/2) ((1+tan^2 t−1)/( (√(1+tan^2 t))))dt =(3/(5(√5)))∫_0 ^(π/2) (√(1+tan^2 t))dt−(3/(5(√5)))∫_0 ^(π/2) (dt/( (√(1+tan^2 t)))) we have ∫_0 ^(π/2) (√(1+tan^2 t))dt =∫_0 ^(π/2) (dt/(cost)) =_(tan((t/2))=y) ∫_0 ^1 ((2dy)/((1+y^2 )((1−y^2 )/(1+y^2 )))) =∫_0 ^1 ((2dy)/(1−y^2 ))=∫_0 ^1 ((1/(1−y))+(1/(1+y)))dy =[ln∣((1+y)/(1−y))∣]_0 ^1 =∞ ∫_0 ^(π/2) (dt/( (√(1+tan^2 ))))=∫_0 ^(π/2) cost dt =[sint]_0 ^(π/2) =1 so this integrale is divdrgente...!](https://www.tinkutara.com/question/Q167585.png)
$$\sqrt{\mathrm{5}}{x}={tant}\:\Rightarrow{I}=\frac{\mathrm{1}}{\:\sqrt{\mathrm{5}}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\mathrm{3}\left(\frac{{tant}}{\:\sqrt{\mathrm{5}}}\right)^{\mathrm{2}} }{\left(\mathrm{1}+{tan}^{\mathrm{2}} \right)^{\frac{\mathrm{3}}{\mathrm{2}}} }\left(\mathrm{1}+{tan}^{\mathrm{2}} {t}\right){dt} \\ $$$$=\frac{\mathrm{3}}{\mathrm{5}\sqrt{\mathrm{5}}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\:\frac{{tan}^{\mathrm{2}} {t}}{\:\sqrt{\mathrm{1}+{tan}^{\mathrm{2}} }}{dt} \\ $$$$=\frac{\mathrm{3}}{\mathrm{5}\sqrt{\mathrm{5}}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\mathrm{1}+{tan}^{\mathrm{2}} {t}−\mathrm{1}}{\:\sqrt{\mathrm{1}+{tan}^{\mathrm{2}} {t}}}{dt} \\ $$$$=\frac{\mathrm{3}}{\mathrm{5}\sqrt{\mathrm{5}}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \sqrt{\mathrm{1}+{tan}^{\mathrm{2}} {t}}{dt}−\frac{\mathrm{3}}{\mathrm{5}\sqrt{\mathrm{5}}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{dt}}{\:\sqrt{\mathrm{1}+{tan}^{\mathrm{2}} {t}}} \\ $$$${we}\:{have}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \sqrt{\mathrm{1}+{tan}^{\mathrm{2}} {t}}{dt} \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{dt}}{{cost}}\:=_{{tan}\left(\frac{{t}}{\mathrm{2}}\right)={y}} \:\:\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{2}{dy}}{\left(\mathrm{1}+{y}^{\mathrm{2}} \right)\frac{\mathrm{1}−{y}^{\mathrm{2}} }{\mathrm{1}+{y}^{\mathrm{2}} }} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{2}{dy}}{\mathrm{1}−{y}^{\mathrm{2}} }=\int_{\mathrm{0}} ^{\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{1}−{y}}+\frac{\mathrm{1}}{\mathrm{1}+{y}}\right){dy} \\ $$$$=\left[{ln}\mid\frac{\mathrm{1}+{y}}{\mathrm{1}−{y}}\mid\right]_{\mathrm{0}} ^{\mathrm{1}} =\infty \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\frac{{dt}}{\:\sqrt{\mathrm{1}+{tan}^{\mathrm{2}} }}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {cost}\:{dt} \\ $$$$=\left[{sint}\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} =\mathrm{1}\:{so}\:{this}\:{integrale}\:{is} \\ $$$${divdrgente}…! \\ $$
