Question Number 98672 by M±th+et+s last updated on 15/Jun/20
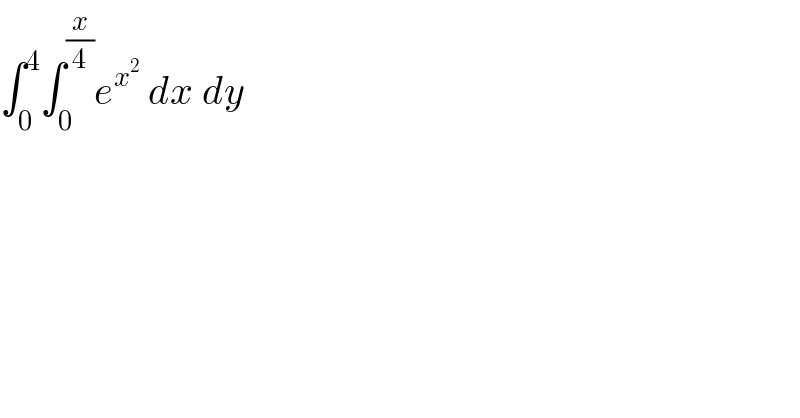
$$\int_{\mathrm{0}} ^{\mathrm{4}} \int_{\mathrm{0}} ^{\frac{{x}}{\mathrm{4}}} {e}^{{x}^{\mathrm{2}} } \:{dx}\:{dy} \\ $$
Answered by Ar Brandon last updated on 16/Jun/20
![Let I=∫_0 ^(x/4) e^x^2 dx........(1) ⇒ I=∫_0 ^(x/4) e^y^2 dy........(2) ⇒I^2 =∫_0 ^(x/4) ∫_0 ^(x/4) e^(x^2 +y^2 ) dxdy=∫_0 ^(π/2) ∫_0 ^(x/4) re^r^2 drdθ ⇒I^2 =[(θ/2)]_0 ^(π/2) [e_ ^r^2^ ]_0 ^(x/4) =(π/4)[ e^(x^2 /(16)) −1_ ] ⇒I=±((√π)/2)[ e^(x^2 /(16)) −1_ ]^(1/2) ⇒∫_0 ^4 ∫_0 ^(x/4) e^x^2 dx dy=±2(√π)[ e^(x^2 /(16)) −1_ ]^(1/2)](https://www.tinkutara.com/question/Q98746.png)
$$\mathrm{Let}\:\mathcal{I}=\int_{\mathrm{0}} ^{\frac{\mathrm{x}}{\mathrm{4}}} \mathrm{e}^{\mathrm{x}^{\mathrm{2}} } \mathrm{dx}……..\left(\mathrm{1}\right) \\ $$$$\Rightarrow\:\:\:\mathcal{I}=\int_{\mathrm{0}} ^{\frac{\mathrm{x}}{\mathrm{4}}} \mathrm{e}^{\mathrm{y}^{\mathrm{2}} } \mathrm{dy}……..\left(\mathrm{2}\right) \\ $$$$\Rightarrow\mathcal{I}^{\mathrm{2}} =\int_{\mathrm{0}} ^{\frac{\mathrm{x}}{\mathrm{4}}} \int_{\mathrm{0}} ^{\frac{\mathrm{x}}{\mathrm{4}}} \mathrm{e}^{\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} } \mathrm{dxdy}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \int_{\mathrm{0}} ^{\frac{\mathrm{x}}{\mathrm{4}}} \mathrm{re}^{\mathrm{r}^{\mathrm{2}} } \mathrm{drd}\theta \\ $$$$\Rightarrow\mathcal{I}^{\mathrm{2}} =\left[\frac{\theta}{\mathrm{2}}\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \left[\mathrm{e}_{} ^{\mathrm{r}^{\mathrm{2}^{} } } \right]_{\mathrm{0}} ^{\frac{\mathrm{x}}{\mathrm{4}}} =\frac{\pi}{\mathrm{4}}\left[\:\mathrm{e}^{\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{16}}} −\mathrm{1}_{} \right] \\ $$$$\Rightarrow\mathcal{I}=\pm\frac{\sqrt{\pi}}{\mathrm{2}}\left[\:\mathrm{e}^{\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{16}}} −\mathrm{1}_{} \right]^{\frac{\mathrm{1}}{\mathrm{2}}} \\ $$$$\Rightarrow\int_{\mathrm{0}} ^{\mathrm{4}} \int_{\mathrm{0}} ^{\frac{{x}}{\mathrm{4}}} {e}^{{x}^{\mathrm{2}} } \:{dx}\:{dy}=\pm\mathrm{2}\sqrt{\pi}\left[\:\mathrm{e}^{\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{16}}} −\mathrm{1}_{} \right]^{\frac{\mathrm{1}}{\mathrm{2}}} \\ $$
Commented by M±th+et+s last updated on 16/Jun/20
$${nice}\:{work}\:{and}\:{correct}\:{thank}\:{you} \\ $$
Commented by Ar Brandon last updated on 16/Jun/20
I don't know if I have done it in the required manner. Can someone kindly check ?
Commented by Ar Brandon last updated on 16/Jun/20
OK, thanks for your feedback.
