Question Number 146746 by mathdanisur last updated on 15/Jul/21
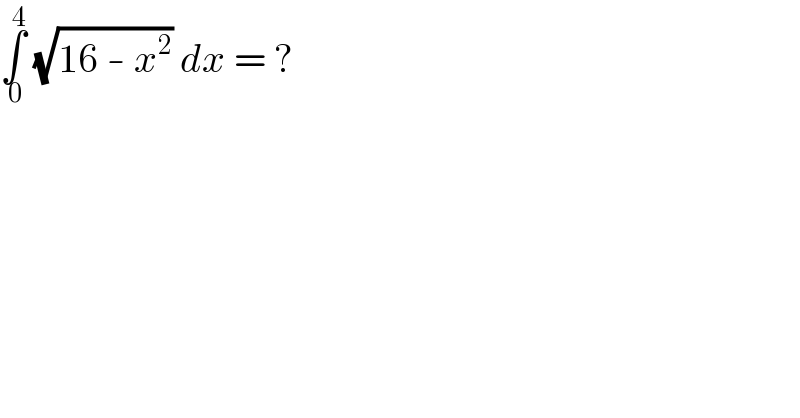
$$\underset{\:\mathrm{0}} {\overset{\:\mathrm{4}} {\int}}\:\sqrt{\mathrm{16}\:-\:{x}^{\mathrm{2}} }\:{dx}\:=\:? \\ $$
Answered by qaz last updated on 15/Jul/21
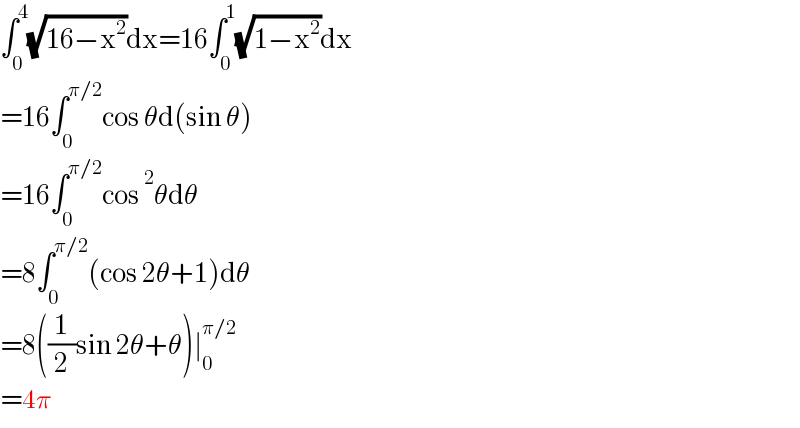
$$\int_{\mathrm{0}} ^{\mathrm{4}} \sqrt{\mathrm{16}−\mathrm{x}^{\mathrm{2}} }\mathrm{dx}=\mathrm{16}\int_{\mathrm{0}} ^{\mathrm{1}} \sqrt{\mathrm{1}−\mathrm{x}^{\mathrm{2}} }\mathrm{dx} \\ $$$$=\mathrm{16}\int_{\mathrm{0}} ^{\pi/\mathrm{2}} \mathrm{cos}\:\theta\mathrm{d}\left(\mathrm{sin}\:\theta\right) \\ $$$$=\mathrm{16}\int_{\mathrm{0}} ^{\pi/\mathrm{2}} \mathrm{cos}\:^{\mathrm{2}} \theta\mathrm{d}\theta \\ $$$$=\mathrm{8}\int_{\mathrm{0}} ^{\pi/\mathrm{2}} \left(\mathrm{cos}\:\mathrm{2}\theta+\mathrm{1}\right)\mathrm{d}\theta \\ $$$$=\mathrm{8}\left(\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin}\:\mathrm{2}\theta+\theta\right)\mid_{\mathrm{0}} ^{\pi/\mathrm{2}} \\ $$$$=\mathrm{4}\pi \\ $$
Commented by mathdanisur last updated on 15/Jul/21

$${thankyou}\:{Ser} \\ $$
Answered by liberty last updated on 15/Jul/21
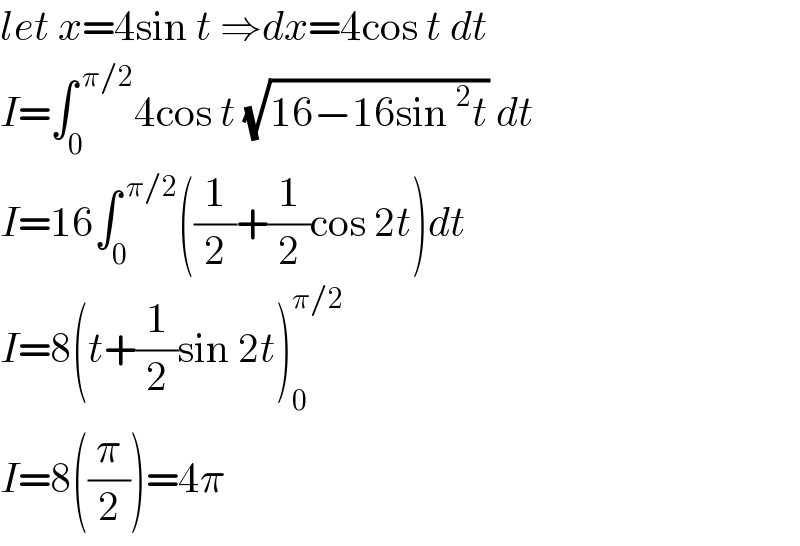
$${let}\:{x}=\mathrm{4sin}\:{t}\:\Rightarrow{dx}=\mathrm{4cos}\:{t}\:{dt} \\ $$$${I}=\int_{\mathrm{0}} ^{\:\pi/\mathrm{2}} \mathrm{4cos}\:{t}\:\sqrt{\mathrm{16}−\mathrm{16sin}\:^{\mathrm{2}} {t}}\:{dt} \\ $$$${I}=\mathrm{16}\int_{\mathrm{0}} ^{\:\pi/\mathrm{2}} \left(\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{cos}\:\mathrm{2}{t}\right){dt} \\ $$$${I}=\mathrm{8}\left({t}+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin}\:\mathrm{2}{t}\right)_{\mathrm{0}} ^{\pi/\mathrm{2}} \\ $$$${I}=\mathrm{8}\left(\frac{\pi}{\mathrm{2}}\right)=\mathrm{4}\pi \\ $$
Commented by mathdanisur last updated on 15/Jul/21

$${thankyou}\:{Ser} \\ $$
Answered by puissant last updated on 15/Jul/21
![x=4cos(u) ⇒ dx=−4sin(u)du K=∫_(π/2) ^0 (√(16−16cos^2 (u)))×(−4sin(u))du =∫_0 ^(π/2) 4sin(u)×4sin(u)du =8∫_0 ^(π/2) 2(((1−cos(2u))/2))du =8[u−(1/2)sin(2u)]_0 ^(π/2) =8((π/2))= 4π...](https://www.tinkutara.com/question/Q146749.png)
$$\mathrm{x}=\mathrm{4cos}\left(\mathrm{u}\right)\:\Rightarrow\:\mathrm{dx}=−\mathrm{4sin}\left(\mathrm{u}\right)\mathrm{du} \\ $$$$\mathrm{K}=\int_{\frac{\pi}{\mathrm{2}}} ^{\mathrm{0}} \sqrt{\mathrm{16}−\mathrm{16cos}^{\mathrm{2}} \left(\mathrm{u}\right)}×\left(−\mathrm{4sin}\left(\mathrm{u}\right)\right)\mathrm{du} \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{4sin}\left(\mathrm{u}\right)×\mathrm{4sin}\left(\mathrm{u}\right)\mathrm{du} \\ $$$$=\mathrm{8}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{2}\left(\frac{\mathrm{1}−\mathrm{cos}\left(\mathrm{2u}\right)}{\mathrm{2}}\right)\mathrm{du} \\ $$$$=\mathrm{8}\left[\mathrm{u}−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin}\left(\mathrm{2u}\right)\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} =\mathrm{8}\left(\frac{\pi}{\mathrm{2}}\right)=\:\mathrm{4}\pi… \\ $$
Commented by mathdanisur last updated on 15/Jul/21

$${thankyou}\:{Ser} \\ $$
Answered by alcohol last updated on 15/Jul/21
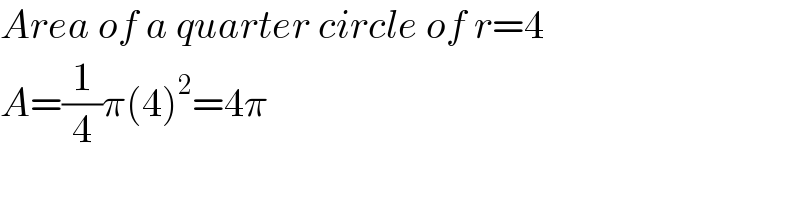
$${Area}\:{of}\:{a}\:{quarter}\:{circle}\:{of}\:{r}=\mathrm{4} \\ $$$${A}=\frac{\mathrm{1}}{\mathrm{4}}\pi\left(\mathrm{4}\right)^{\mathrm{2}} =\mathrm{4}\pi \\ $$
Commented by mathdanisur last updated on 15/Jul/21

$${thanks}\:{Ser} \\ $$
