Question Number 81549 by jagoll last updated on 13/Feb/20
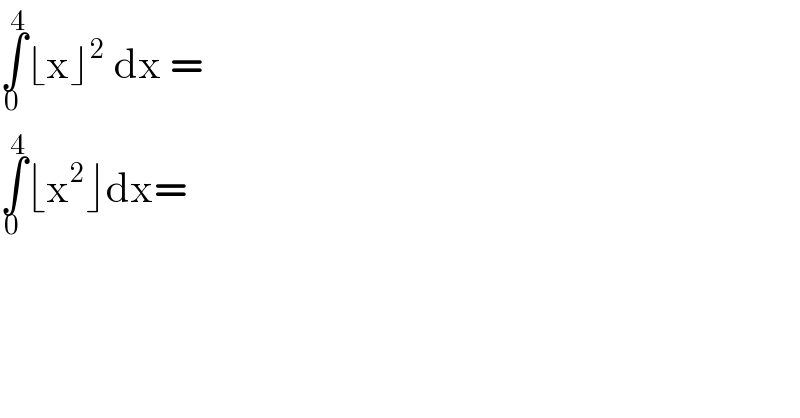
$$\underset{\mathrm{0}} {\overset{\mathrm{4}} {\int}}\lfloor\mathrm{x}\rfloor^{\mathrm{2}} \:\mathrm{dx}\:=\: \\ $$$$\underset{\mathrm{0}} {\overset{\mathrm{4}} {\int}}\lfloor\mathrm{x}^{\mathrm{2}} \rfloor\mathrm{dx}= \\ $$
Commented by jagoll last updated on 14/Feb/20
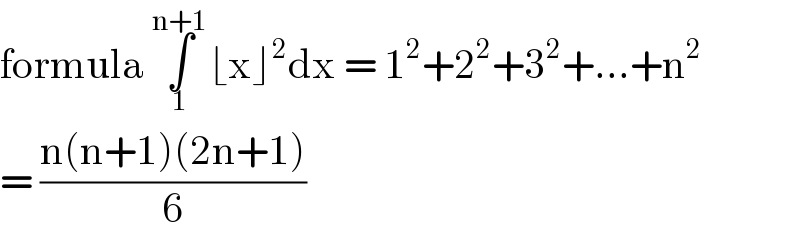
$$\mathrm{formula}\:\underset{\mathrm{1}} {\overset{\mathrm{n}+\mathrm{1}} {\int}}\lfloor\mathrm{x}\rfloor^{\mathrm{2}} \mathrm{dx}\:=\:\mathrm{1}^{\mathrm{2}} +\mathrm{2}^{\mathrm{2}} +\mathrm{3}^{\mathrm{2}} +…+\mathrm{n}^{\mathrm{2}} \\ $$$$=\:\frac{\mathrm{n}\left(\mathrm{n}+\mathrm{1}\right)\left(\mathrm{2n}+\mathrm{1}\right)}{\mathrm{6}} \\ $$
Commented by jagoll last updated on 14/Feb/20
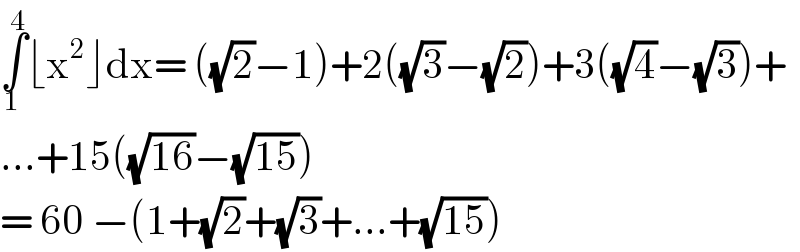
$$\underset{\mathrm{1}} {\overset{\mathrm{4}} {\int}}\lfloor\mathrm{x}^{\mathrm{2}} \rfloor\mathrm{dx}=\:\left(\sqrt{\mathrm{2}}−\mathrm{1}\right)+\mathrm{2}\left(\sqrt{\mathrm{3}}−\sqrt{\mathrm{2}}\right)+\mathrm{3}\left(\sqrt{\mathrm{4}}−\sqrt{\mathrm{3}}\right)+ \\ $$$$…+\mathrm{15}\left(\sqrt{\mathrm{16}}−\sqrt{\mathrm{15}}\right) \\ $$$$=\:\mathrm{60}\:−\left(\mathrm{1}+\sqrt{\mathrm{2}}+\sqrt{\mathrm{3}}+…+\sqrt{\mathrm{15}}\right) \\ $$
Commented by mathmax by abdo last updated on 14/Feb/20
![∫_0 ^4 [x]^2 dx =Σ_(k=0) ^3 ∫_k ^(k+1) k^2 dx =Σ_(k=0) ^3 k^2 =1^2 +2^2 +3^2 =1+4 +9=14](https://www.tinkutara.com/question/Q81707.png)
$$\int_{\mathrm{0}} ^{\mathrm{4}} \left[{x}\right]^{\mathrm{2}} \:{dx}\:=\sum_{{k}=\mathrm{0}} ^{\mathrm{3}} \:\int_{{k}} ^{{k}+\mathrm{1}} {k}^{\mathrm{2}} \:{dx}\:=\sum_{{k}=\mathrm{0}} ^{\mathrm{3}} \:{k}^{\mathrm{2}} \:=\mathrm{1}^{\mathrm{2}} \:+\mathrm{2}^{\mathrm{2}} \:+\mathrm{3}^{\mathrm{2}} =\mathrm{1}+\mathrm{4}\:+\mathrm{9}=\mathrm{14} \\ $$
Commented by mathmax by abdo last updated on 14/Feb/20
![∫_0 ^4 [x^2 ]dx =Σ_(k=1) ^(15) ∫_(√k) ^(√(k+1)) [x^2 ]dx =Σ_(k=1) ^(15) ∫_(√k) ^(√(k+1)) kdx =Σ_(k=1) ^(15) k((√(k+1))−(√k)) =(√2)−1 +2((√3)−(√2))+3((√4)−(√3)) +....+15((√(16))−(√(15)))](https://www.tinkutara.com/question/Q81708.png)
$$\int_{\mathrm{0}} ^{\mathrm{4}} \left[{x}^{\mathrm{2}} \right]{dx}\:=\sum_{{k}=\mathrm{1}} ^{\mathrm{15}} \:\int_{\sqrt{{k}}} ^{\sqrt{{k}+\mathrm{1}}} \:\:\left[{x}^{\mathrm{2}} \right]{dx}\:=\sum_{{k}=\mathrm{1}} ^{\mathrm{15}} \:\int_{\sqrt{{k}}} ^{\sqrt{{k}+\mathrm{1}}} {kdx} \\ $$$$=\sum_{{k}=\mathrm{1}} ^{\mathrm{15}} {k}\left(\sqrt{{k}+\mathrm{1}}−\sqrt{{k}}\right)\:=\sqrt{\mathrm{2}}−\mathrm{1}\:+\mathrm{2}\left(\sqrt{\mathrm{3}}−\sqrt{\mathrm{2}}\right)+\mathrm{3}\left(\sqrt{\mathrm{4}}−\sqrt{\mathrm{3}}\right) \\ $$$$+….+\mathrm{15}\left(\sqrt{\mathrm{16}}−\sqrt{\mathrm{15}}\right) \\ $$
Commented by mathmax by abdo last updated on 14/Feb/20
![genrally ∫_1 ^n [x^2 ]dx =Σ_(k=1) ^(n−1) ∫_(√k) ^(√(k+1)) k dx =Σ_(k=1) ^(n−1) k((√(k+1))−(√k))=(√2)−1 +2((√3)−(√2))+...+(n−1)((√n)−(√(n−1))) =Σ_(k=1) ^(n−1) (k/( (√k)+(√(k+1)))) =(1/(1+(√2))) +(2/( (√2)+(√3))) +....+((n−1)/( (√(n−1)) +(√n)))](https://www.tinkutara.com/question/Q81710.png)
$${genrally}\:\int_{\mathrm{1}} ^{{n}} \left[{x}^{\mathrm{2}} \right]{dx}\:=\sum_{{k}=\mathrm{1}} ^{{n}−\mathrm{1}} \:\int_{\sqrt{{k}}} ^{\sqrt{{k}+\mathrm{1}}} {k}\:{dx} \\ $$$$=\sum_{{k}=\mathrm{1}} ^{{n}−\mathrm{1}} {k}\left(\sqrt{{k}+\mathrm{1}}−\sqrt{{k}}\right)=\sqrt{\mathrm{2}}−\mathrm{1}\:+\mathrm{2}\left(\sqrt{\mathrm{3}}−\sqrt{\mathrm{2}}\right)+…+\left({n}−\mathrm{1}\right)\left(\sqrt{{n}}−\sqrt{{n}−\mathrm{1}}\right) \\ $$$$=\sum_{{k}=\mathrm{1}} ^{{n}−\mathrm{1}} \:\frac{{k}}{\:\sqrt{{k}}+\sqrt{{k}+\mathrm{1}}}\:=\frac{\mathrm{1}}{\mathrm{1}+\sqrt{\mathrm{2}}}\:+\frac{\mathrm{2}}{\:\sqrt{\mathrm{2}}+\sqrt{\mathrm{3}}}\:+….+\frac{{n}−\mathrm{1}}{\:\sqrt{{n}−\mathrm{1}}\:+\sqrt{{n}}} \\ $$
