Question Number 124352 by Mammadli last updated on 02/Dec/20

$$\underset{\mathrm{0}} {\overset{\mathrm{4}\pi} {\int}}\parallel{cosx}\parallel=? \\ $$
Commented by mr W last updated on 02/Dec/20
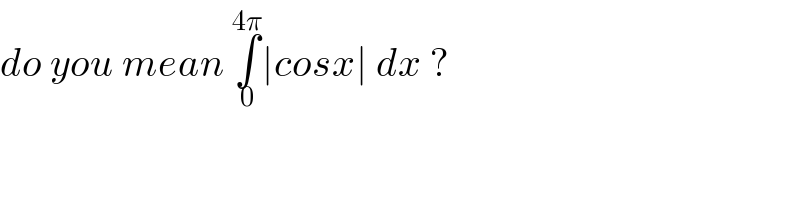
$${do}\:{you}\:{mean}\:\underset{\mathrm{0}} {\overset{\mathrm{4}\pi} {\int}}\mid{cosx}\mid\:{dx}\:? \\ $$
Commented by Mammadli last updated on 02/Dec/20
Dear Ser, as I mentioned, it was given..
Commented by mr W last updated on 02/Dec/20
![∫_0 ^(4π) ∣cosx∣ dx =8 ∫_0 ^(π/2) cos x dx =8[sin x]_0 ^(π/2) =8(1−0) =8](https://www.tinkutara.com/question/Q124366.png)
$$\underset{\mathrm{0}} {\overset{\mathrm{4}\pi} {\int}}\mid{cosx}\mid\:{dx}\: \\ $$$$=\mathrm{8}\:\underset{\mathrm{0}} {\overset{\frac{\pi}{\mathrm{2}}} {\int}}{cos}\:{x}\:{dx}\: \\ $$$$=\mathrm{8}\left[\mathrm{sin}\:{x}\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \\ $$$$=\mathrm{8}\left(\mathrm{1}−\mathrm{0}\right) \\ $$$$=\mathrm{8} \\ $$
