Question Number 180095 by BHOOPENDRA last updated on 07/Nov/22
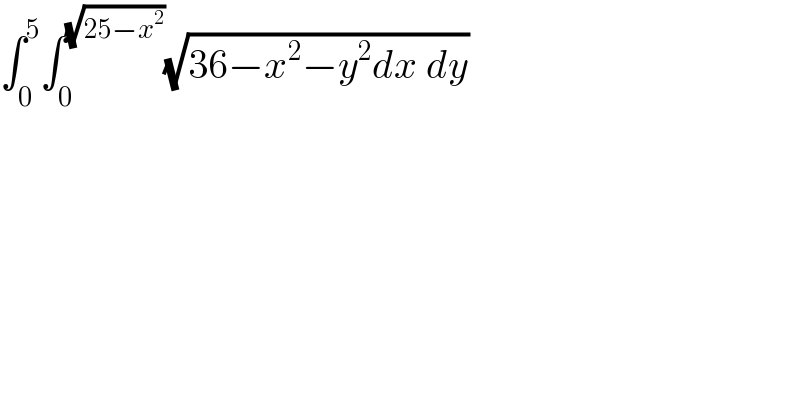
$$\int_{\mathrm{0}} ^{\mathrm{5}} \int_{\mathrm{0}} ^{\sqrt{\mathrm{25}−{x}^{\mathrm{2}} }} \sqrt{\mathrm{36}−{x}^{\mathrm{2}} −{y}^{\mathrm{2}} {dx}\:{dy}} \\ $$
Answered by mr W last updated on 07/Nov/22
![I=∫_0 ^(π/2) (∫_0 ^5 (√(36−r^2 ))rdr)dθ =(π/2)×(1/2)∫_0 ^5 (√(36−r^2 ))d(r^2 ) =(π/6)[(36−r^2 )^(3/2) ]_5 ^0 =(π/6)(216−11(√(11)))](https://www.tinkutara.com/question/Q180096.png)
$${I}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \left(\int_{\mathrm{0}} ^{\mathrm{5}} \sqrt{\mathrm{36}−{r}^{\mathrm{2}} }{rdr}\right){d}\theta \\ $$$$=\frac{\pi}{\mathrm{2}}×\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{5}} \sqrt{\mathrm{36}−{r}^{\mathrm{2}} }{d}\left({r}^{\mathrm{2}} \right) \\ $$$$=\frac{\pi}{\mathrm{6}}\left[\left(\mathrm{36}−{r}^{\mathrm{2}} \right)^{\frac{\mathrm{3}}{\mathrm{2}}} \right]_{\mathrm{5}} ^{\mathrm{0}} \\ $$$$=\frac{\pi}{\mathrm{6}}\left(\mathrm{216}−\mathrm{11}\sqrt{\mathrm{11}}\right) \\ $$
