Question Number 86247 by M±th+et£s last updated on 27/Mar/20
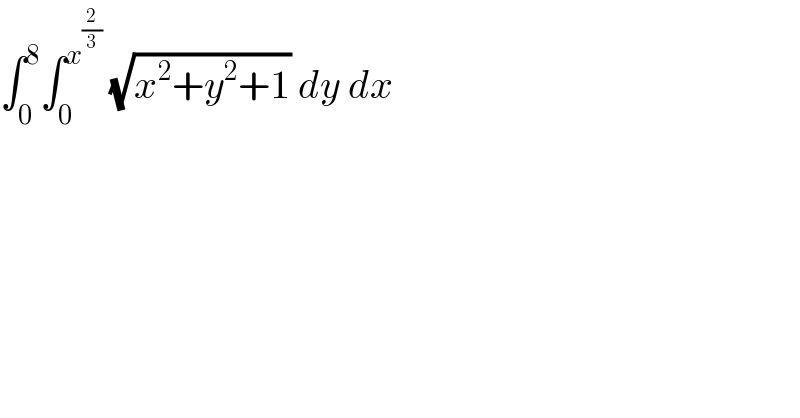
$$\int_{\mathrm{0}} ^{\mathrm{8}} \int_{\mathrm{0}} ^{{x}^{\frac{\mathrm{2}}{\mathrm{3}}} } \:\sqrt{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} +\mathrm{1}}\:{dy}\:{dx} \\ $$
Commented by mathmax by abdo last updated on 27/Mar/20
![A =∫_0 ^8 (∫_0 ^x^(2/3) (√(y^2 +x^2 +1))dy)dx =∫_0 ^8 A(x)dx A(x)=∫_0 ^x^(2/3) (√(y^2 +x^2 +1))dy we do the cyangement y =(√(x^2 +1))sh(t) ⇒t =argsh((y/( (√(x^2 +1))))) =ln((y/( (√(x^2 +1))))+(√(1+(y^2 /(x^2 +1))))) A(x)=∫_0 ^(ln((x^(2/3) /( (√(x^2 +1))))+(√(1+(x^(4/3) /(x^2 +1)))))) (√(x^(2 ) +1))ch(t)(√(x^2 +1))ch(t)dt =(x^2 +1) ∫_0 ^(ln(((x^(2/3) +(√(x^2 +1+x^(4/3) )))/( (√(x^2 +1)))))) (((1+ch(2t))/2))dt =(1/2)(x^2 +1)ln(((x^(2/3) +(√(x^2 +1+x^(4/3) )))/( (√(x^2 +1)))))+(1/4)(x^2 +1)[sh(2t)]_0 ^(...) =(1/2)(x^2 +1)ln(((x^(2/3) +(√(x^2 +1 +x^(4/3) )))/( (√(x^2 +1)))))+(1/4)(x^2 +1)[ ((e^(2t) −e^(−2t) )/2)]_0 ^(...) be continued....](https://www.tinkutara.com/question/Q86268.png)
$${A}\:=\int_{\mathrm{0}} ^{\mathrm{8}} \left(\int_{\mathrm{0}} ^{{x}^{\frac{\mathrm{2}}{\mathrm{3}}} } \sqrt{{y}^{\mathrm{2}} \:+{x}^{\mathrm{2}} +\mathrm{1}}{dy}\right){dx}\:=\int_{\mathrm{0}} ^{\mathrm{8}} \:{A}\left({x}\right){dx}\: \\ $$$${A}\left({x}\right)=\int_{\mathrm{0}} ^{{x}^{\frac{\mathrm{2}}{\mathrm{3}}} } \sqrt{{y}^{\mathrm{2}} \:+{x}^{\mathrm{2}} \:+\mathrm{1}}{dy}\:\:{we}\:{do}\:{the}\:{cyangement}\:{y}\:=\sqrt{{x}^{\mathrm{2}} \:+\mathrm{1}}{sh}\left({t}\right) \\ $$$$\Rightarrow{t}\:={argsh}\left(\frac{{y}}{\:\sqrt{{x}^{\mathrm{2}} \:+\mathrm{1}}}\right)\:={ln}\left(\frac{{y}}{\:\sqrt{{x}^{\mathrm{2}} \:+\mathrm{1}}}+\sqrt{\mathrm{1}+\frac{{y}^{\mathrm{2}} }{{x}^{\mathrm{2}} \:+\mathrm{1}}}\right) \\ $$$${A}\left({x}\right)=\int_{\mathrm{0}} ^{{ln}\left(\frac{{x}^{\frac{\mathrm{2}}{\mathrm{3}}} }{\:\sqrt{{x}^{\mathrm{2}} \:+\mathrm{1}}}+\sqrt{\mathrm{1}+\frac{{x}^{\frac{\mathrm{4}}{\mathrm{3}}} }{{x}^{\mathrm{2}} \:+\mathrm{1}}}\right)} \sqrt{{x}^{\mathrm{2}\:} +\mathrm{1}}{ch}\left({t}\right)\sqrt{{x}^{\mathrm{2}} \:+\mathrm{1}}{ch}\left({t}\right){dt} \\ $$$$=\left({x}^{\mathrm{2}} \:+\mathrm{1}\right)\:\int_{\mathrm{0}} ^{{ln}\left(\frac{{x}^{\frac{\mathrm{2}}{\mathrm{3}}} \:+\sqrt{{x}^{\mathrm{2}} \:+\mathrm{1}+{x}^{\frac{\mathrm{4}}{\mathrm{3}}} }}{\:\sqrt{{x}^{\mathrm{2}} \:+\mathrm{1}}}\right)} \left(\frac{\mathrm{1}+{ch}\left(\mathrm{2}{t}\right)}{\mathrm{2}}\right){dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left({x}^{\mathrm{2}} \:+\mathrm{1}\right){ln}\left(\frac{{x}^{\frac{\mathrm{2}}{\mathrm{3}}} \:+\sqrt{{x}^{\mathrm{2}} \:+\mathrm{1}+{x}^{\frac{\mathrm{4}}{\mathrm{3}}} }}{\:\sqrt{{x}^{\mathrm{2}} \:+\mathrm{1}}}\right)+\frac{\mathrm{1}}{\mathrm{4}}\left({x}^{\mathrm{2}} \:+\mathrm{1}\right)\left[{sh}\left(\mathrm{2}{t}\right)\right]_{\mathrm{0}} ^{…} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left({x}^{\mathrm{2}} \:+\mathrm{1}\right){ln}\left(\frac{{x}^{\frac{\mathrm{2}}{\mathrm{3}}} \:+\sqrt{{x}^{\mathrm{2}} \:+\mathrm{1}\:+{x}^{\frac{\mathrm{4}}{\mathrm{3}}} }}{\:\sqrt{{x}^{\mathrm{2}} \:+\mathrm{1}}}\right)+\frac{\mathrm{1}}{\mathrm{4}}\left({x}^{\mathrm{2}} \:+\mathrm{1}\right)\left[\:\frac{{e}^{\mathrm{2}{t}} −{e}^{−\mathrm{2}{t}} }{\mathrm{2}}\right]_{\mathrm{0}} ^{…} \\ $$$${be}\:{continued}…. \\ $$
Commented by M±th+et£s last updated on 27/Mar/20
$${god}\:{bless}\:{you}\:{sir}\:.{thanks} \\ $$
Commented by mathmax by abdo last updated on 28/Mar/20

$$\:{you}\:{are}\:{welcome}\:{sir}. \\ $$
