Question Number 17009 by arnabpapu550@gmail.com last updated on 29/Jun/17
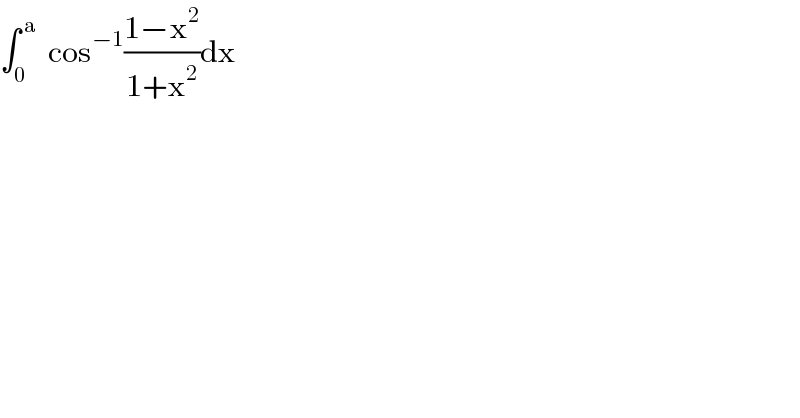
$$\int_{\mathrm{0}} ^{\:\mathrm{a}} \:\:\mathrm{cos}^{−\mathrm{1}} \frac{\mathrm{1}−\mathrm{x}^{\mathrm{2}} }{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\mathrm{dx} \\ $$
Commented by prakash jain last updated on 29/Jun/17
![x=tan u ((1−x^2 )/(1+x^2 ))=((1−tan^2 u)/(1+tan^2 u))=cos 2u dx=sec^2 udu ∫2usec^2 u du =2utan u−∫tan udu] =2[utan u−2ln cos u] cos u=(1/(sec u))=(1/( (√(1+tan^2 j))))=(1/( (√(1+x^2 )))) =2[xtan^(−1) x−ln (1/( (√(1+x^2 ))))] =2x[tan^(−1) x+ln (√(1+x^2 )) ] =2xtan^(−1) x+ln (1+x^2 ) A tan^(−1) x=θ x=tan θ⇒cos 2θ=((1−tan^2 θ)/(1+tan^2 θ))=((1−x^2 )/(1+x^2 )) 2tan^(−1) x=2θ=cos^(−1) (cos 2θ) =cos^(−1) ((1−x^2 )/(1+x^2 )) A can also be written as xcos^(−1) ((1−x^2 )/(1+x^2 ))+ln (1+x^2 )](https://www.tinkutara.com/question/Q17015.png)
$${x}=\mathrm{tan}\:{u} \\ $$$$\frac{\mathrm{1}−{x}^{\mathrm{2}} }{\mathrm{1}+{x}^{\mathrm{2}} }=\frac{\mathrm{1}−\mathrm{tan}^{\mathrm{2}} {u}}{\mathrm{1}+\mathrm{tan}^{\mathrm{2}} {u}}=\mathrm{cos}\:\mathrm{2}{u} \\ $$$${dx}=\mathrm{sec}^{\mathrm{2}} {udu} \\ $$$$\int\mathrm{2}{u}\mathrm{sec}^{\mathrm{2}} {u}\:{du} \\ $$$$\left.=\mathrm{2}{u}\mathrm{tan}\:{u}−\int\mathrm{tan}\:{udu}\right] \\ $$$$=\mathrm{2}\left[{u}\mathrm{tan}\:{u}−\mathrm{2ln}\:\mathrm{cos}\:{u}\right] \\ $$$$\mathrm{cos}\:{u}=\frac{\mathrm{1}}{\mathrm{sec}\:{u}}=\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}+\mathrm{tan}^{\mathrm{2}} {j}}}=\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }} \\ $$$$=\mathrm{2}\left[{x}\mathrm{tan}^{−\mathrm{1}} {x}−\mathrm{ln}\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}\right] \\ $$$$=\mathrm{2}{x}\left[\mathrm{tan}^{−\mathrm{1}} {x}+\mathrm{ln}\:\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\:\right] \\ $$$$=\mathrm{2}{x}\mathrm{tan}^{−\mathrm{1}} {x}+\mathrm{ln}\:\left(\mathrm{1}+{x}^{\mathrm{2}} \right)\:\:\:\:\:\:{A} \\ $$$${tan}^{−\mathrm{1}} {x}=\theta \\ $$$${x}=\mathrm{tan}\:\theta\Rightarrow\mathrm{cos}\:\mathrm{2}\theta=\frac{\mathrm{1}−\mathrm{tan}^{\mathrm{2}} \theta}{\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \theta}=\frac{\mathrm{1}−{x}^{\mathrm{2}} }{\mathrm{1}+{x}^{\mathrm{2}} } \\ $$$$\mathrm{2tan}^{−\mathrm{1}} {x}=\mathrm{2}\theta=\mathrm{cos}^{−\mathrm{1}} \left(\mathrm{cos}\:\mathrm{2}\theta\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{cos}^{−\mathrm{1}} \frac{\mathrm{1}−{x}^{\mathrm{2}} }{\mathrm{1}+{x}^{\mathrm{2}} } \\ $$$${A}\:{can}\:{also}\:{be}\:{written}\:{as} \\ $$$${x}\mathrm{cos}^{−\mathrm{1}} \frac{\mathrm{1}−{x}^{\mathrm{2}} }{\mathrm{1}+{x}^{\mathrm{2}} }+\mathrm{ln}\:\left(\mathrm{1}+{x}^{\mathrm{2}} \right) \\ $$
