Question Number 150840 by mathdanisur last updated on 15/Aug/21

$$\underset{\:\mathrm{0}} {\overset{\:\infty} {\int}}\:\frac{\mathrm{arctan}\left(\mathrm{x}\right)}{\mathrm{x}\left(\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}\right)}\:\mathrm{dx}\:=\:? \\ $$
Answered by mathmax by abdo last updated on 17/Aug/21
![f(a)=∫_0 ^∞ ((arctan(ax))/(x(x^2 +x+1)))dx (a>0) ⇒ f^′ (a)=∫_0 ^∞ (x/(x(1+a^2 x^2 )(x^2 +x+1)))dx =∫_0 ^∞ (dx/((a^2 x^2 +1)(x^2 +x+1)))=_(ax=t) ∫_0 ^∞ (dt/(a(t^2 +1)((t^2 /a^2 ) +(t/a)+1))) =a∫_0 ^∞ (dt/((t^2 +1)(t^2 +at+a^2 ))) let decompose F(t)=(1/((t^2 +1)(t^2 +at+a^2 )))=((αt+β)/(t^2 +1)) +((mt+n)/(t^2 +at+a^2 )) lim_(t→+∞) tF(t)=0 =α+m ⇒m=−α ⇒ F(t)=((αt+β)/(t^2 +1))+((−αt+n)/(t^2 +at +a^2 )) ⇒ (αt+β)(t^2 +at+a^2 )+(t^2 +1)(−αt +n)=1 ⇒ αt^3 +αat^2 +αa^(2 ) +βt^(2 ) +βat+βa^2 −αt^3 +nt^2 −αt+n=1 ⇒ (αa+n)t^2 +(βa−α)t +αa^2 +βa^2 +n=1 ⇒ αa+n=0 and βa−α=0 and αa^2 +βa^(2 ) +n=1 ⇒ n=−αa and βa=α and αa^2 +αa−αa=1 ⇒α=(1/a^2 ) ⇒ n=−(1/a) and β=(1/a^3 ) ⇒ F(t)=(((1/a^2 )t+(1/a^3 ))/(t^2 +1)) +((−(1/a^2 )t−(1/a))/(t^2 +at +a^2 )) F(t)=(1/a^3 )×((at+1)/(t^2 +1))−(1/a^2 )((t+a)/(t^2 +at +a^2 )) ⇒ f^′ (a) =(1/a^2 )∫_0 ^∞ ((at+1)/(t^2 +1))dt−(1/a)∫_0 ^∞ ((t+a)/(t^2 +at+a^2 )) =(1/(2a))∫_0 ^∞ ((2t)/(t^(2 ) +1))dt+(π/(2a^2 ))−(1/(2a))∫_0 ^∞ ((2t+a+a)/(t^2 +at+a^2 ))dt =(1/(2a))[ln(((t^2 +1)/(t^2 +at+a^2 )))]_0 ^∞ +(π/(2a^2 ))−(1/2)∫_0 ^∞ (dt/(t^2 +at+a^2 )) =−(1/(2a))ln((1/a^2 ))+(π/(2a^2 ))−(1/2)∫_0 ^∞ (..(√()dx)) ((lna)/a)+(π/(2a^2 ))−(1/2)∫_0 ^∞ (dt/(t^2 +at+a^2 )) ∫_0 ^∞ (dt/(t^2 +at+a^2 ))=∫_0 ^∞ (dt/(t^(2 ) +2(a/2)t +(a^2 /4)+a^2 −(a^2 /4))) =∫_0 ^∞ (dt/((t+(a/2))^(2 ) +(3/4)a^2 ))=_(t+(a/2)=((√3)/2)az) (4/(3a^2 )) ∫_(1/( (√3))) ^∞ (1/(1+z^2 ))×((√3)/2)adz =(2/(a(√3)))((π/2)−arctan((1/( (√3))))).....be continued...](https://www.tinkutara.com/question/Q150956.png)
$$\mathrm{f}\left(\mathrm{a}\right)=\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{arctan}\left(\mathrm{ax}\right)}{\mathrm{x}\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{x}+\mathrm{1}\right)}\mathrm{dx}\:\:\left(\mathrm{a}>\mathrm{0}\right)\:\Rightarrow \\ $$$$\mathrm{f}^{'} \left(\mathrm{a}\right)=\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{x}}{\mathrm{x}\left(\mathrm{1}+\mathrm{a}^{\mathrm{2}} \mathrm{x}^{\mathrm{2}} \right)\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{x}+\mathrm{1}\right)}\mathrm{dx} \\ $$$$=\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{dx}}{\left(\mathrm{a}^{\mathrm{2}} \mathrm{x}^{\mathrm{2}} \:+\mathrm{1}\right)\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{x}+\mathrm{1}\right)}=_{\mathrm{ax}=\mathrm{t}} \:\:\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{\mathrm{dt}}{\mathrm{a}\left(\mathrm{t}^{\mathrm{2}} \:+\mathrm{1}\right)\left(\frac{\mathrm{t}^{\mathrm{2}} }{\mathrm{a}^{\mathrm{2}} }\:+\frac{\mathrm{t}}{\mathrm{a}}+\mathrm{1}\right)} \\ $$$$=\mathrm{a}\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{dt}}{\left(\mathrm{t}^{\mathrm{2}} \:+\mathrm{1}\right)\left(\mathrm{t}^{\mathrm{2}} +\mathrm{at}+\mathrm{a}^{\mathrm{2}} \right)} \\ $$$$\mathrm{let}\:\mathrm{decompose}\:\mathrm{F}\left(\mathrm{t}\right)=\frac{\mathrm{1}}{\left(\mathrm{t}^{\mathrm{2}} +\mathrm{1}\right)\left(\mathrm{t}^{\mathrm{2}} \:+\mathrm{at}+\mathrm{a}^{\mathrm{2}} \right)}=\frac{\alpha\mathrm{t}+\beta}{\mathrm{t}^{\mathrm{2}} \:+\mathrm{1}}\:+\frac{\mathrm{mt}+\mathrm{n}}{\mathrm{t}^{\mathrm{2}} \:+\mathrm{at}+\mathrm{a}^{\mathrm{2}} } \\ $$$$\mathrm{lim}_{\mathrm{t}\rightarrow+\infty} \mathrm{tF}\left(\mathrm{t}\right)=\mathrm{0}\:=\alpha+\mathrm{m}\:\Rightarrow\mathrm{m}=−\alpha\:\Rightarrow \\ $$$$\mathrm{F}\left(\mathrm{t}\right)=\frac{\alpha\mathrm{t}+\beta}{\mathrm{t}^{\mathrm{2}} \:+\mathrm{1}}+\frac{−\alpha\mathrm{t}+\mathrm{n}}{\mathrm{t}^{\mathrm{2}} \:+\mathrm{at}\:+\mathrm{a}^{\mathrm{2}} }\:\Rightarrow \\ $$$$\left(\alpha\mathrm{t}+\beta\right)\left(\mathrm{t}^{\mathrm{2}} \:+\mathrm{at}+\mathrm{a}^{\mathrm{2}} \right)+\left(\mathrm{t}^{\mathrm{2}} \:+\mathrm{1}\right)\left(−\alpha\mathrm{t}\:+\mathrm{n}\right)=\mathrm{1}\:\Rightarrow \\ $$$$\alpha\mathrm{t}^{\mathrm{3}} \:+\alpha\mathrm{at}^{\mathrm{2}} \:+\alpha\mathrm{a}^{\mathrm{2}\:} \:+\beta\mathrm{t}^{\mathrm{2}\:} +\beta\mathrm{at}+\beta\mathrm{a}^{\mathrm{2}} \:−\alpha\mathrm{t}^{\mathrm{3}} +\mathrm{nt}^{\mathrm{2}} −\alpha\mathrm{t}+\mathrm{n}=\mathrm{1}\:\Rightarrow \\ $$$$\left(\alpha\mathrm{a}+\mathrm{n}\right)\mathrm{t}^{\mathrm{2}} \:+\left(\beta\mathrm{a}−\alpha\right)\mathrm{t}\:+\alpha\mathrm{a}^{\mathrm{2}} \:+\beta\mathrm{a}^{\mathrm{2}} +\mathrm{n}=\mathrm{1}\:\Rightarrow \\ $$$$\alpha\mathrm{a}+\mathrm{n}=\mathrm{0}\:\mathrm{and}\:\beta\mathrm{a}−\alpha=\mathrm{0}\:\mathrm{and}\:\alpha\mathrm{a}^{\mathrm{2}} \:+\beta\mathrm{a}^{\mathrm{2}\:} +\mathrm{n}=\mathrm{1}\:\Rightarrow \\ $$$$\mathrm{n}=−\alpha\mathrm{a}\:\:\mathrm{and}\:\beta\mathrm{a}=\alpha\:\mathrm{and}\:\alpha\mathrm{a}^{\mathrm{2}} \:+\alpha\mathrm{a}−\alpha\mathrm{a}=\mathrm{1}\:\Rightarrow\alpha=\frac{\mathrm{1}}{\mathrm{a}^{\mathrm{2}} }\:\Rightarrow \\ $$$$\mathrm{n}=−\frac{\mathrm{1}}{\mathrm{a}}\:\:\mathrm{and}\:\beta=\frac{\mathrm{1}}{\mathrm{a}^{\mathrm{3}} }\:\Rightarrow \\ $$$$\mathrm{F}\left(\mathrm{t}\right)=\frac{\frac{\mathrm{1}}{\mathrm{a}^{\mathrm{2}} }\mathrm{t}+\frac{\mathrm{1}}{\mathrm{a}^{\mathrm{3}} }}{\mathrm{t}^{\mathrm{2}} \:+\mathrm{1}}\:+\frac{−\frac{\mathrm{1}}{\mathrm{a}^{\mathrm{2}} }\mathrm{t}−\frac{\mathrm{1}}{\mathrm{a}}}{\mathrm{t}^{\mathrm{2}} \:+\mathrm{at}\:+\mathrm{a}^{\mathrm{2}} } \\ $$$$\mathrm{F}\left(\mathrm{t}\right)=\frac{\mathrm{1}}{\mathrm{a}^{\mathrm{3}} }×\frac{\mathrm{at}+\mathrm{1}}{\mathrm{t}^{\mathrm{2}} \:+\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{a}^{\mathrm{2}} }\frac{\mathrm{t}+\mathrm{a}}{\mathrm{t}^{\mathrm{2}} \:+\mathrm{at}\:+\mathrm{a}^{\mathrm{2}} }\:\Rightarrow \\ $$$$\mathrm{f}^{'} \left(\mathrm{a}\right)\:=\frac{\mathrm{1}}{\mathrm{a}^{\mathrm{2}} }\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{at}+\mathrm{1}}{\mathrm{t}^{\mathrm{2}} \:+\mathrm{1}}\mathrm{dt}−\frac{\mathrm{1}}{\mathrm{a}}\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{t}+\mathrm{a}}{\mathrm{t}^{\mathrm{2}} \:+\mathrm{at}+\mathrm{a}^{\mathrm{2}} } \\ $$$$=\frac{\mathrm{1}}{\mathrm{2a}}\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{2t}}{\mathrm{t}^{\mathrm{2}\:} +\mathrm{1}}\mathrm{dt}+\frac{\pi}{\mathrm{2a}^{\mathrm{2}} }−\frac{\mathrm{1}}{\mathrm{2a}}\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{2t}+\mathrm{a}+\mathrm{a}}{\mathrm{t}^{\mathrm{2}} \:+\mathrm{at}+\mathrm{a}^{\mathrm{2}} }\mathrm{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2a}}\left[\mathrm{ln}\left(\frac{\mathrm{t}^{\mathrm{2}} +\mathrm{1}}{\mathrm{t}^{\mathrm{2}} \:+\mathrm{at}+\mathrm{a}^{\mathrm{2}} }\right)\right]_{\mathrm{0}} ^{\infty} \:+\frac{\pi}{\mathrm{2a}^{\mathrm{2}} }−\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{dt}}{\mathrm{t}^{\mathrm{2}} \:+\mathrm{at}+\mathrm{a}^{\mathrm{2}} } \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2a}}\mathrm{ln}\left(\frac{\mathrm{1}}{\mathrm{a}^{\mathrm{2}} }\right)+\frac{\pi}{\mathrm{2a}^{\mathrm{2}} }−\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\infty} \left(..\sqrt{\left.\right)\mathrm{dx}}\right. \\ $$$$\frac{\mathrm{lna}}{\mathrm{a}}+\frac{\pi}{\mathrm{2a}^{\mathrm{2}} }−\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{dt}}{\mathrm{t}^{\mathrm{2}} \:+\mathrm{at}+\mathrm{a}^{\mathrm{2}} } \\ $$$$\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{dt}}{\mathrm{t}^{\mathrm{2}} \:+\mathrm{at}+\mathrm{a}^{\mathrm{2}} }=\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{dt}}{\mathrm{t}^{\mathrm{2}\:} +\mathrm{2}\frac{\mathrm{a}}{\mathrm{2}}\mathrm{t}\:+\frac{\mathrm{a}^{\mathrm{2}} }{\mathrm{4}}+\mathrm{a}^{\mathrm{2}} −\frac{\mathrm{a}^{\mathrm{2}} }{\mathrm{4}}} \\ $$$$=\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{dt}}{\left(\mathrm{t}+\frac{\mathrm{a}}{\mathrm{2}}\right)^{\mathrm{2}\:} +\frac{\mathrm{3}}{\mathrm{4}}\mathrm{a}^{\mathrm{2}} }=_{\mathrm{t}+\frac{\mathrm{a}}{\mathrm{2}}=\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\mathrm{az}} \:\frac{\mathrm{4}}{\mathrm{3a}^{\mathrm{2}} }\:\:\int_{\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}} ^{\infty} \:\frac{\mathrm{1}}{\mathrm{1}+\mathrm{z}^{\mathrm{2}} }×\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\mathrm{adz} \\ $$$$=\frac{\mathrm{2}}{\mathrm{a}\sqrt{\mathrm{3}}}\left(\frac{\pi}{\mathrm{2}}−\mathrm{arctan}\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right)\right)…..\mathrm{be}\:\mathrm{continued}… \\ $$
Commented by mathdanisur last updated on 18/Aug/21
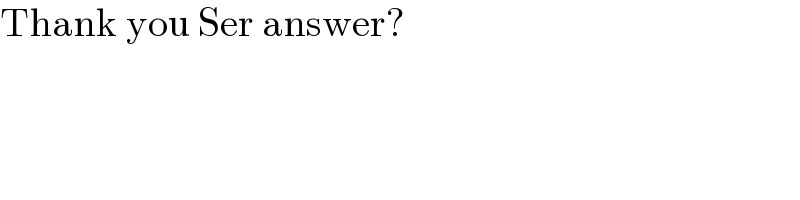
$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{Ser}\:\mathrm{answer}? \\ $$
