0-cos-ax-sin-bx-x-2-dx-0-1-2sin-2-ax-2-1-2sin-2-bx-2-x-2-dx-2-0-sin-bx-2-x-2-dx-1-2-0-

Question Number 173486 by mnjuly1970 last updated on 12/Jul/22

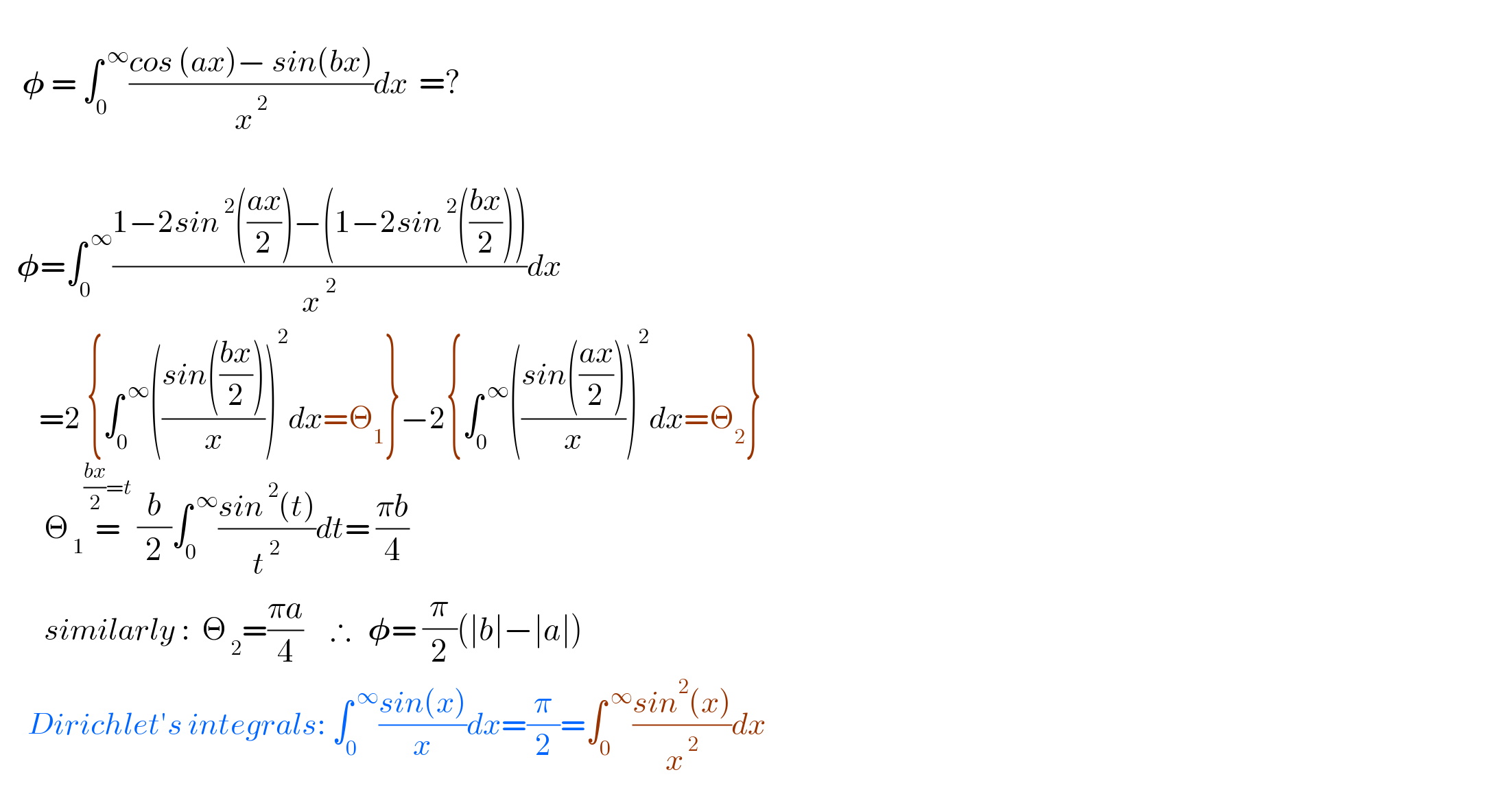
𝛗 = ∫_0 ^( ∞) ((cos (ax)− sin(bx))/x^( 2) )dx =? 𝛗=∫_0 ^( ∞) ((1−2sin^( 2) (((ax)/2))−(1−2sin^( 2) (((bx)/2))))/(x^2 ))dx =2 {∫_0 ^( ∞) (((sin(((bx)/2)))/x))^2 dx=Θ_1 }−2{∫_0 ^( ∞) (((sin(((ax)/2)))/x))^2 dx=Θ_2 } Θ_( 1) =^(((bx)/2)=t) (b/2)∫_0 ^( ∞) ((sin^( 2) (t))/t^( 2) )dt= ((πb)/4) similarly : Θ_( 2) =((πa)/4) ∴ 𝛗= (π/2)(∣b∣−∣a∣) Dirichlet′s integrals: ∫_0 ^( ∞) ((sin(x))/x)dx=(π/2)=∫_0 ^( ∞) ((sin^2 (x))/x^( 2) )dx

$$ \\ $$$$\:\:\:\:\boldsymbol{\phi}\:=\:\int_{\mathrm{0}} ^{\:\infty} \frac{{cos}\:\left({ax}\right)−\:{sin}\left({bx}\right)}{{x}^{\:\mathrm{2}} }{dx}\:\:=? \\ $$$$\:\:\: \\ $$$$\:\:\:\boldsymbol{\phi}=\int_{\mathrm{0}} ^{\:\infty} \frac{\mathrm{1}−\mathrm{2}{sin}^{\:\mathrm{2}} \left(\frac{{ax}}{\mathrm{2}}\right)−\left(\mathrm{1}−\mathrm{2}{sin}^{\:\mathrm{2}} \left(\frac{{bx}}{\mathrm{2}}\right)\right)}{{x}\:^{\mathrm{2}} }{dx} \\ $$$$\:\:\:\:\:\:\:=\mathrm{2}\:\left\{\int_{\mathrm{0}} ^{\:\infty} \left(\frac{{sin}\left(\frac{{bx}}{\mathrm{2}}\right)}{{x}}\right)^{\mathrm{2}} {dx}=\Theta_{\mathrm{1}} \right\}−\mathrm{2}\left\{\int_{\mathrm{0}} ^{\:\infty} \left(\frac{{sin}\left(\frac{{ax}}{\mathrm{2}}\right)}{{x}}\right)^{\mathrm{2}} {dx}=\Theta_{\mathrm{2}} \right\} \\ $$$$\:\:\:\:\:\:\:\:\Theta_{\:\mathrm{1}} \overset{\frac{{bx}}{\mathrm{2}}={t}} {=}\:\frac{{b}}{\mathrm{2}}\int_{\mathrm{0}} ^{\:\infty} \frac{{sin}^{\:\mathrm{2}} \left({t}\right)}{{t}^{\:\mathrm{2}} }{dt}=\:\frac{\pi{b}}{\mathrm{4}}\: \\ $$$$\:\:\:\:\:\:\:\:{similarly}\::\:\:\Theta_{\:\mathrm{2}} =\frac{\pi{a}}{\mathrm{4}}\:\:\:\:\:\therefore\:\:\:\boldsymbol{\phi}=\:\frac{\pi}{\mathrm{2}}\left(\mid{b}\mid−\mid{a}\mid\right)\: \\ $$$$\:\:\:\:\:{Dirichlet}'{s}\:{integrals}:\:\int_{\mathrm{0}} ^{\:\infty} \frac{{sin}\left({x}\right)}{{x}}{dx}=\frac{\pi}{\mathrm{2}}=\int_{\mathrm{0}} ^{\:\infty} \frac{{sin}^{\mathrm{2}} \left({x}\right)}{{x}^{\:\mathrm{2}} }{dx} \\ $$

Commented by mokys last updated on 15/Jul/22

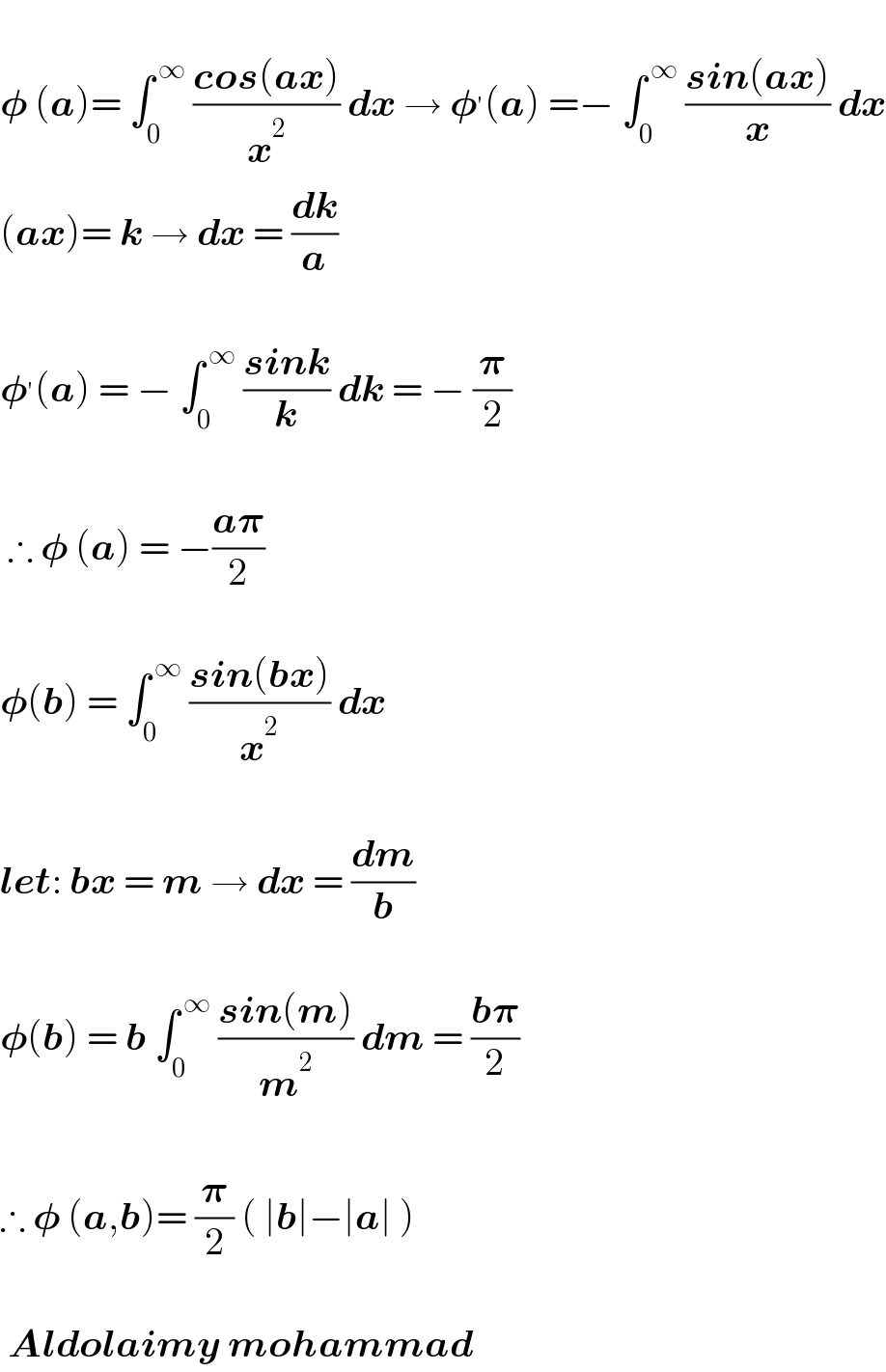
𝛗 (a)= ∫_0 ^( ∞) ((cos(ax))/x^2 ) dx → 𝛗^′ (a) =− ∫_0 ^( ∞) ((sin(ax))/x) dx (ax)= k → dx = (dk/a) 𝛗^′ (a) = − ∫_0 ^( ∞) ((sink)/k) dk = − (𝛑/2) ∴ 𝛗 (a) = −((a𝛑)/2) 𝛗(b) = ∫_0 ^( ∞) ((sin(bx))/x^2 ) dx let: bx = m → dx = (dm/b) 𝛗(b) = b ∫_0 ^( ∞) ((sin(m))/m^2 ) dm = ((b𝛑)/2) ∴ 𝛗 (a,b)= (𝛑/2) ( ∣b∣−∣a∣ ) Aldolaimy mohammad

$$ \\ $$$$\boldsymbol{\phi}\:\left(\boldsymbol{{a}}\right)=\:\int_{\mathrm{0}} ^{\:\infty} \:\frac{\boldsymbol{{cos}}\left(\boldsymbol{{ax}}\right)}{\boldsymbol{{x}}^{\mathrm{2}} }\:\boldsymbol{{dx}}\:\rightarrow\:\boldsymbol{\phi}^{'} \left(\boldsymbol{{a}}\right)\:=−\:\int_{\mathrm{0}} ^{\:\infty} \:\frac{\boldsymbol{{sin}}\left(\boldsymbol{{ax}}\right)}{\boldsymbol{{x}}}\:\boldsymbol{{dx}} \\ $$$$\left(\boldsymbol{{ax}}\right)=\:\boldsymbol{{k}}\:\rightarrow\:\boldsymbol{{dx}}\:=\:\frac{\boldsymbol{{dk}}}{\boldsymbol{{a}}} \\ $$$$ \\ $$$$\boldsymbol{\phi}^{'} \left(\boldsymbol{{a}}\right)\:=\:−\:\int_{\mathrm{0}} ^{\:\infty} \:\frac{\boldsymbol{{sink}}}{\boldsymbol{{k}}}\:\boldsymbol{{dk}}\:=\:−\:\frac{\boldsymbol{\pi}}{\mathrm{2}} \\ $$$$ \\ $$$$\:\therefore\:\boldsymbol{\phi}\:\left(\boldsymbol{{a}}\right)\:=\:−\frac{\boldsymbol{{a}\pi}}{\mathrm{2}} \\ $$$$ \\ $$$$\boldsymbol{\phi}\left(\boldsymbol{{b}}\right)\:=\:\int_{\mathrm{0}} ^{\:\infty} \:\frac{\boldsymbol{{sin}}\left(\boldsymbol{{bx}}\right)}{\boldsymbol{{x}}^{\mathrm{2}} }\:\boldsymbol{{dx}}\: \\ $$$$ \\ $$$$\boldsymbol{{let}}:\:\boldsymbol{{bx}}\:=\:\boldsymbol{{m}}\:\rightarrow\:\boldsymbol{{dx}}\:=\:\frac{\boldsymbol{{dm}}}{\boldsymbol{{b}}} \\ $$$$ \\ $$$$\boldsymbol{\phi}\left(\boldsymbol{{b}}\right)\:=\:\boldsymbol{{b}}\:\int_{\mathrm{0}} ^{\:\infty} \:\frac{\boldsymbol{{sin}}\left(\boldsymbol{{m}}\right)}{\boldsymbol{{m}}^{\mathrm{2}} }\:\boldsymbol{{dm}}\:=\:\frac{\boldsymbol{{b}\pi}}{\mathrm{2}} \\ $$$$ \\ $$$$\therefore\:\boldsymbol{\phi}\:\left(\boldsymbol{{a}},\boldsymbol{{b}}\right)=\:\frac{\boldsymbol{\pi}}{\mathrm{2}}\:\left(\:\mid\boldsymbol{{b}}\mid−\mid\boldsymbol{{a}}\mid\:\right) \\ $$$$ \\ $$$$\:\boldsymbol{{Aldolaimy}}\:\boldsymbol{{mohammad}} \\ $$

Facebook Tweet Pin

0-cos-ax-sin-bx-x-2-dx-0-1-2sin-2-ax-2-1-2sin-2-bx-2-x-2-dx-2-0-sin-bx-2-x-2-dx-1-2-0-

Leave a Reply Cancel reply