Question Number 101970 by Rohit@Thakur last updated on 05/Jul/20
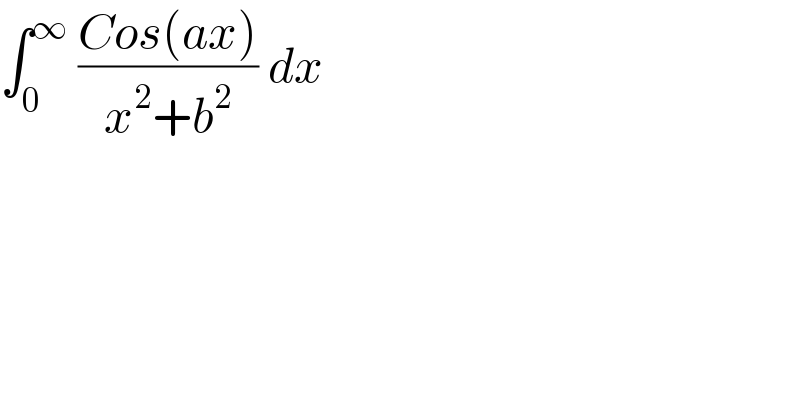
$$\int_{\mathrm{0}} ^{\infty} \:\frac{{Cos}\left({ax}\right)}{{x}^{\mathrm{2}} +{b}^{\mathrm{2}} }\:{dx} \\ $$
Answered by mathmax by abdo last updated on 06/Jul/20
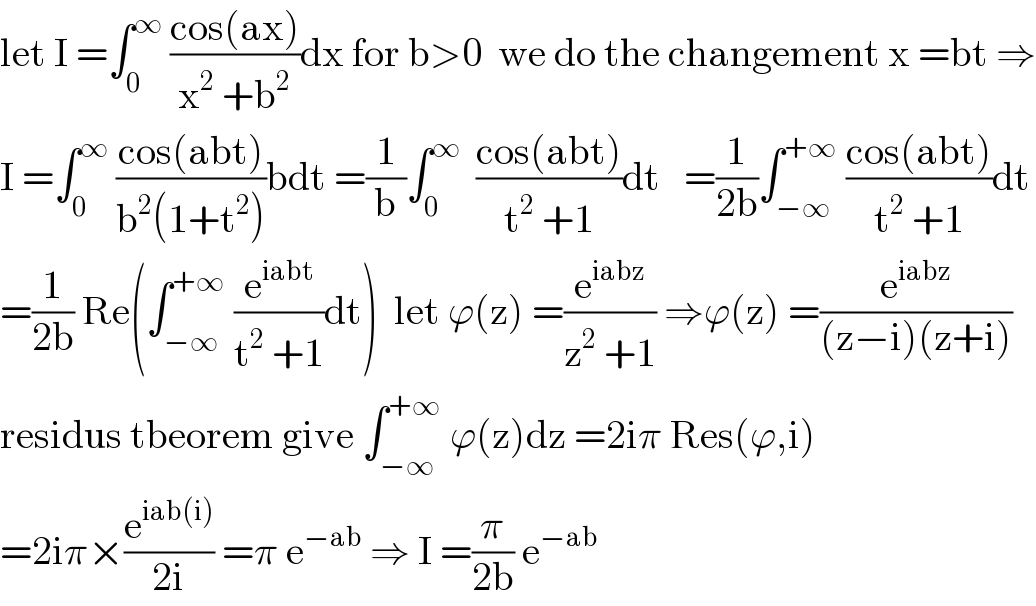
$$\mathrm{let}\:\mathrm{I}\:=\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{cos}\left(\mathrm{ax}\right)}{\mathrm{x}^{\mathrm{2}} \:+\mathrm{b}^{\mathrm{2}} }\mathrm{dx}\:\mathrm{for}\:\mathrm{b}>\mathrm{0}\:\:\mathrm{we}\:\mathrm{do}\:\mathrm{the}\:\mathrm{changement}\:\mathrm{x}\:=\mathrm{bt}\:\Rightarrow \\ $$$$\mathrm{I}\:=\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{cos}\left(\mathrm{abt}\right)}{\mathrm{b}^{\mathrm{2}} \left(\mathrm{1}+\mathrm{t}^{\mathrm{2}} \right)}\mathrm{bdt}\:=\frac{\mathrm{1}}{\mathrm{b}}\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{cos}\left(\mathrm{abt}\right)}{\mathrm{t}^{\mathrm{2}} \:+\mathrm{1}}\mathrm{dt}\:\:\:=\frac{\mathrm{1}}{\mathrm{2b}}\int_{−\infty} ^{+\infty} \:\frac{\mathrm{cos}\left(\mathrm{abt}\right)}{\mathrm{t}^{\mathrm{2}} \:+\mathrm{1}}\mathrm{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2b}}\:\mathrm{Re}\left(\int_{−\infty} ^{+\infty} \:\frac{\mathrm{e}^{\mathrm{iabt}} }{\mathrm{t}^{\mathrm{2}} \:+\mathrm{1}}\mathrm{dt}\right)\:\:\mathrm{let}\:\varphi\left(\mathrm{z}\right)\:=\frac{\mathrm{e}^{\mathrm{iabz}} }{\mathrm{z}^{\mathrm{2}} \:+\mathrm{1}}\:\Rightarrow\varphi\left(\mathrm{z}\right)\:=\frac{\mathrm{e}^{\mathrm{iabz}} }{\left(\mathrm{z}−\mathrm{i}\right)\left(\mathrm{z}+\mathrm{i}\right)} \\ $$$$\mathrm{residus}\:\mathrm{tbeorem}\:\mathrm{give}\:\int_{−\infty} ^{+\infty} \:\varphi\left(\mathrm{z}\right)\mathrm{dz}\:=\mathrm{2i}\pi\:\mathrm{Res}\left(\varphi,\mathrm{i}\right) \\ $$$$=\mathrm{2i}\pi×\frac{\mathrm{e}^{\mathrm{iab}\left(\mathrm{i}\right)} }{\mathrm{2i}}\:=\pi\:\mathrm{e}^{−\mathrm{ab}} \:\Rightarrow\:\mathrm{I}\:=\frac{\pi}{\mathrm{2b}}\:\mathrm{e}^{−\mathrm{ab}} \\ $$
