Question Number 85346 by naka3546 last updated on 21/Mar/20
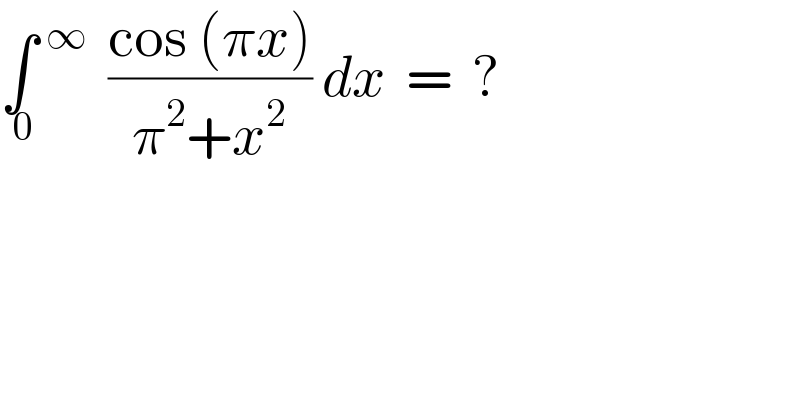
$$\underset{\:\mathrm{0}} {\int}\:\overset{\infty} {\:}\:\:\frac{\mathrm{cos}\:\left(\pi{x}\right)}{\pi^{\mathrm{2}} +{x}^{\mathrm{2}} }\:{dx}\:\:=\:\:? \\ $$
Commented by abdomathmax last updated on 21/Mar/20
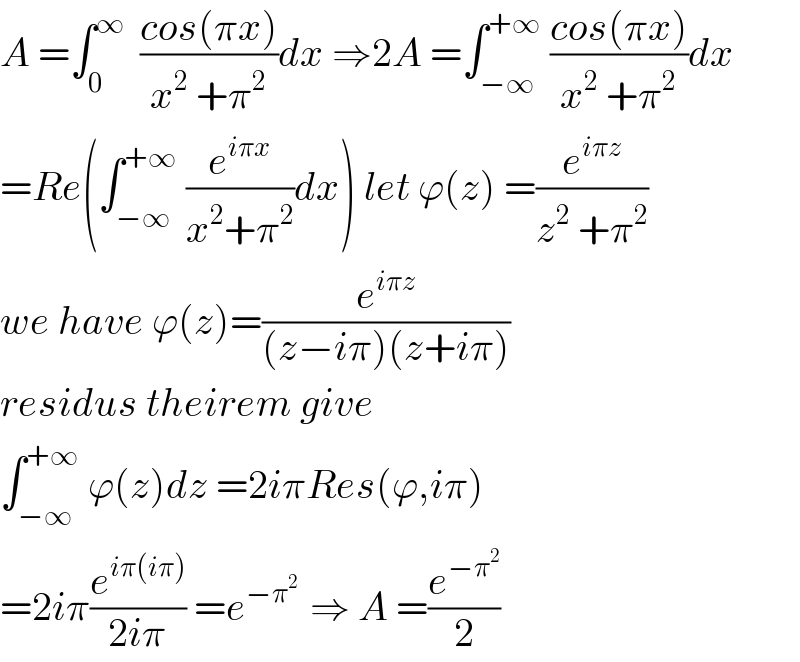
$${A}\:=\int_{\mathrm{0}} ^{\infty} \:\:\frac{{cos}\left(\pi{x}\right)}{{x}^{\mathrm{2}} \:+\pi^{\mathrm{2}} }{dx}\:\Rightarrow\mathrm{2}{A}\:=\int_{−\infty} ^{+\infty} \:\frac{{cos}\left(\pi{x}\right)}{{x}^{\mathrm{2}} \:+\pi^{\mathrm{2}} }{dx} \\ $$$$={Re}\left(\int_{−\infty} ^{+\infty} \:\frac{{e}^{{i}\pi{x}} }{{x}^{\mathrm{2}} +\pi^{\mathrm{2}} }{dx}\right)\:{let}\:\varphi\left({z}\right)\:=\frac{{e}^{{i}\pi{z}} }{{z}^{\mathrm{2}} \:+\pi^{\mathrm{2}} } \\ $$$${we}\:{have}\:\varphi\left({z}\right)=\frac{{e}^{{i}\pi{z}} }{\left({z}−{i}\pi\right)\left({z}+{i}\pi\right)} \\ $$$${residus}\:{theirem}\:{give}\: \\ $$$$\int_{−\infty} ^{+\infty} \:\varphi\left({z}\right){dz}\:=\mathrm{2}{i}\pi{Res}\left(\varphi,{i}\pi\right) \\ $$$$=\mathrm{2}{i}\pi\frac{{e}^{{i}\pi\left({i}\pi\right)} }{\mathrm{2}{i}\pi}\:={e}^{−\pi^{\mathrm{2}} \:} \:\Rightarrow\:{A}\:=\frac{{e}^{−\pi^{\mathrm{2}} } }{\mathrm{2}} \\ $$
Answered by M±th+et£s last updated on 21/Mar/20
![f(p)=∫_0 ^∞ ((cos(pπx))/(π^2 +x^2 )) dx⇒⇒⇒⌊(f(p))=∫_0 ^∞ ∫_0 ^∞ ((cos(pπx))/(π^2 +x^2 )) dx dp =∫_0 ^∞ (1/(π^2 +x^2 ))∫_0 ^∞ e^(−ps) cos(pπx) dx dp =∫_0 ^∞ (1/((π^2 +x^2 )))((s/(s^2 +π^2 x^2 )))dx =(s/(s−π^4 ))∫_0 ^∞ ((s^2 +π^2 x^2 −π^4 −π^2 x^2 )/((π^2 +x^2 )(s^2 +π^2 x^2 ))) dx (s/(s^2 −π^4 ))∫((1/(π^2 +x^2 ))−(π^2 /(s^2 +π^2 x^2 )))dx (s/(s^2 −π^4 ))[(1/π)tan^(−1) (x/π) −(π/s)tan^(−1) ((πx)/s)]_0 ^∞ (s/(s^2 −π^4 ))[(1/2)−(π^2 /(2s))] (s/(s^2 −π^4 ))(((s−π^2 )/(2s)))=(1/(2(s+π^2 ))) f(p)=⌊^(−1) ((1/(s+π^2 ))) =(1/2)e^(−π^2 )](https://www.tinkutara.com/question/Q85419.png)
$${f}\left({p}\right)=\int_{\mathrm{0}} ^{\infty} \frac{{cos}\left({p}\pi{x}\right)}{\pi^{\mathrm{2}} +{x}^{\mathrm{2}} }\:{dx}\Rightarrow\Rightarrow\Rightarrow\lfloor\left({f}\left({p}\right)\right)=\int_{\mathrm{0}} ^{\infty} \int_{\mathrm{0}} ^{\infty} \frac{{cos}\left({p}\pi{x}\right)}{\pi^{\mathrm{2}} +{x}^{\mathrm{2}} }\:{dx}\:{dp} \\ $$$$=\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{1}}{\pi^{\mathrm{2}} +{x}^{\mathrm{2}} }\int_{\mathrm{0}} ^{\infty} {e}^{−{ps}} \:{cos}\left({p}\pi{x}\right)\:{dx}\:{dp} \\ $$$$=\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{1}}{\left(\pi^{\mathrm{2}} +{x}^{\mathrm{2}} \right)}\left(\frac{{s}}{{s}^{\mathrm{2}} +\pi^{\mathrm{2}} {x}^{\mathrm{2}} }\right){dx} \\ $$$$=\frac{{s}}{{s}−\pi^{\mathrm{4}} }\int_{\mathrm{0}} ^{\infty} \frac{{s}^{\mathrm{2}} +\pi^{\mathrm{2}} {x}^{\mathrm{2}} −\pi^{\mathrm{4}} −\pi^{\mathrm{2}} {x}^{\mathrm{2}} }{\left(\pi^{\mathrm{2}} +{x}^{\mathrm{2}} \right)\left({s}^{\mathrm{2}} +\pi^{\mathrm{2}} {x}^{\mathrm{2}} \right)}\:{dx} \\ $$$$\frac{{s}}{{s}^{\mathrm{2}} −\pi^{\mathrm{4}} }\int\left(\frac{\mathrm{1}}{\pi^{\mathrm{2}} +{x}^{\mathrm{2}} }−\frac{\pi^{\mathrm{2}} }{{s}^{\mathrm{2}} +\pi^{\mathrm{2}} {x}^{\mathrm{2}} }\right){dx} \\ $$$$\frac{{s}}{{s}^{\mathrm{2}} −\pi^{\mathrm{4}} }\left[\frac{\mathrm{1}}{\pi}{tan}^{−\mathrm{1}} \frac{{x}}{\pi}\:−\frac{\pi}{{s}}{tan}^{−\mathrm{1}} \frac{\pi{x}}{{s}}\right]_{\mathrm{0}} ^{\infty} \\ $$$$\frac{{s}}{{s}^{\mathrm{2}} −\pi^{\mathrm{4}} }\left[\frac{\mathrm{1}}{\mathrm{2}}−\frac{\pi^{\mathrm{2}} }{\mathrm{2}{s}}\right] \\ $$$$\frac{{s}}{{s}^{\mathrm{2}} −\pi^{\mathrm{4}} }\left(\frac{{s}−\pi^{\mathrm{2}} }{\mathrm{2}{s}}\right)=\frac{\mathrm{1}}{\mathrm{2}\left({s}+\pi^{\mathrm{2}} \right)} \\ $$$${f}\left({p}\right)=\lfloor^{−\mathrm{1}} \left(\frac{\mathrm{1}}{{s}+\pi^{\mathrm{2}} }\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}{e}^{−\pi^{\mathrm{2}} \:\:\:} \\ $$$$ \\ $$$$ \\ $$
