Question Number 151599 by mathdanisur last updated on 22/Aug/21
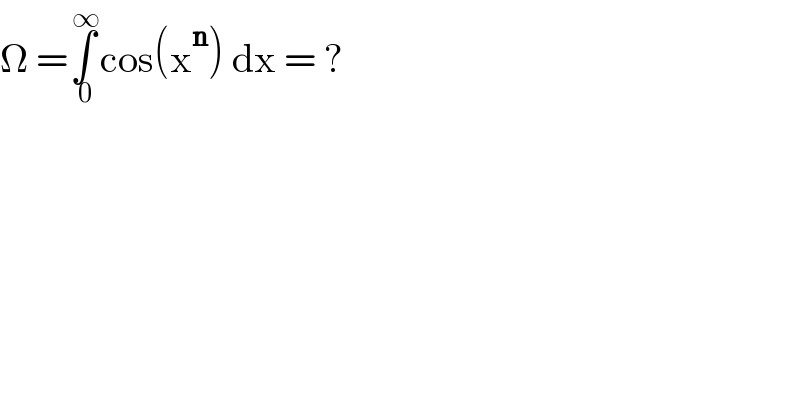
$$\Omega\:=\underset{\:\mathrm{0}} {\overset{\:\infty} {\int}}\mathrm{cos}\left(\mathrm{x}^{\boldsymbol{\mathrm{n}}} \right)\:\mathrm{dx}\:=\:? \\ $$
Answered by Lordose last updated on 22/Aug/21
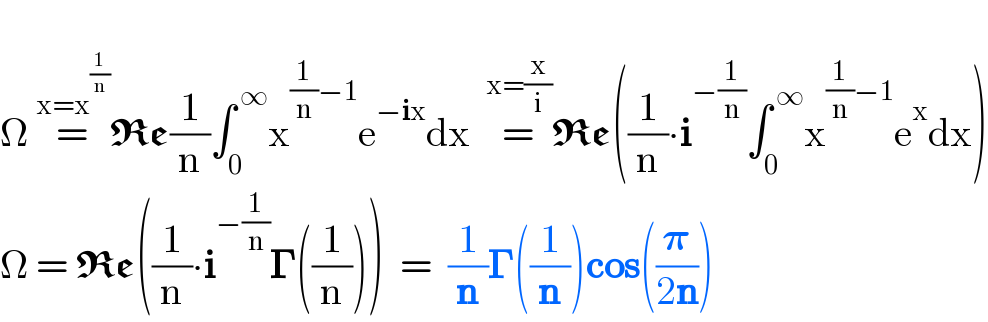
$$ \\ $$$$\Omega\:\overset{\mathrm{x}=\mathrm{x}^{\frac{\mathrm{1}}{\mathrm{n}}} } {=}\boldsymbol{\mathfrak{Re}}\frac{\mathrm{1}}{\mathrm{n}}\int_{\mathrm{0}} ^{\:\infty} \mathrm{x}^{\frac{\mathrm{1}}{\mathrm{n}}−\mathrm{1}} \mathrm{e}^{−\boldsymbol{\mathrm{i}}\mathrm{x}} \mathrm{dx}\:\:\overset{\mathrm{x}=\frac{\mathrm{x}}{\mathrm{i}}} {=}\boldsymbol{\mathfrak{Re}}\left(\frac{\mathrm{1}}{\mathrm{n}}\centerdot\boldsymbol{\mathrm{i}}^{−\frac{\mathrm{1}}{\mathrm{n}}} \int_{\mathrm{0}} ^{\:\infty} \mathrm{x}^{\frac{\mathrm{1}}{\mathrm{n}}−\mathrm{1}} \mathrm{e}^{\mathrm{x}} \mathrm{dx}\right) \\ $$$$\Omega\:=\:\boldsymbol{\mathfrak{Re}}\left(\frac{\mathrm{1}}{\mathrm{n}}\centerdot\boldsymbol{\mathrm{i}}^{−\frac{\mathrm{1}}{\mathrm{n}}} \boldsymbol{\Gamma}\left(\frac{\mathrm{1}}{\mathrm{n}}\right)\right)\:\:=\:\:\frac{\mathrm{1}}{\boldsymbol{\mathrm{n}}}\boldsymbol{\Gamma}\left(\frac{\mathrm{1}}{\boldsymbol{\mathrm{n}}}\right)\boldsymbol{\mathrm{cos}}\left(\frac{\boldsymbol{\pi}}{\mathrm{2}\boldsymbol{\mathrm{n}}}\right) \\ $$
