Menu Close

0-cosx-x-2-1-dx-

Tinku Tara 0 Comments
Pin




Question Number 103721 by Dwaipayan Shikari last updated on 16/Jul/20
∫_0 ^∞ ((cosx)/(x^2 +1))dx
$$\int_{\mathrm{0}} ^{\infty} \frac{{cosx}}{{x}^{\mathrm{2}} +\mathrm{1}}{dx} \\ $$
Answered by Ar Brandon last updated on 16/Jul/20
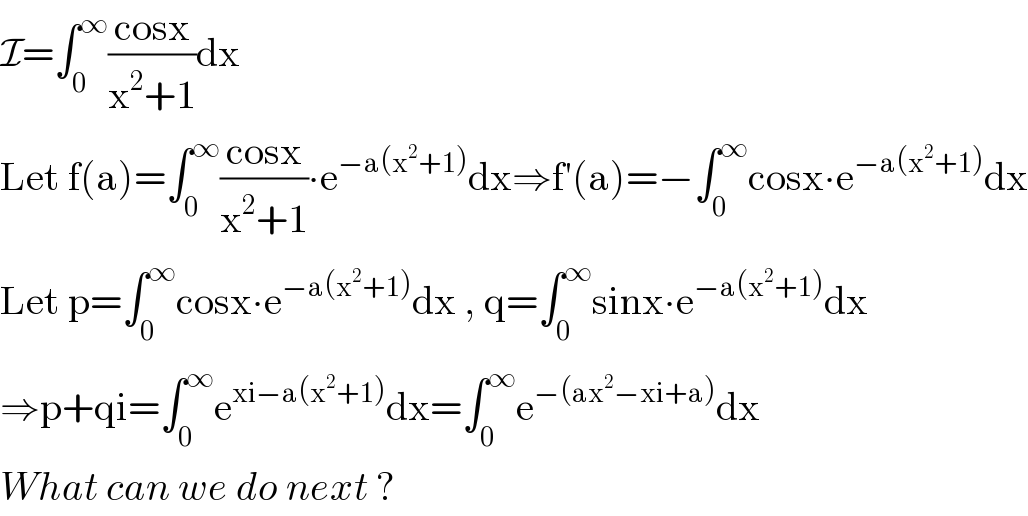
I=∫_0 ^∞ ((cosx)/(x^2 +1))dx Let f(a)=∫_0 ^∞ ((cosx)/(x^2 +1))∙e^(−a(x^2 +1)) dx⇒f′(a)=−∫_0 ^∞ cosx∙e^(−a(x^2 +1)) dx Let p=∫_0 ^∞ cosx∙e^(−a(x^2 +1)) dx , q=∫_0 ^∞ sinx∙e^(−a(x^2 +1)) dx ⇒p+qi=∫_0 ^∞ e^(xi−a(x^2 +1)) dx=∫_0 ^∞ e^(−(ax^2 −xi+a)) dx What can we do next ?
$$\mathcal{I}=\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{cosx}}{\mathrm{x}^{\mathrm{2}} +\mathrm{1}}\mathrm{dx} \\ $$$$\mathrm{Let}\:\mathrm{f}\left(\mathrm{a}\right)=\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{cosx}}{\mathrm{x}^{\mathrm{2}} +\mathrm{1}}\centerdot\mathrm{e}^{−\mathrm{a}\left(\mathrm{x}^{\mathrm{2}} +\mathrm{1}\right)} \mathrm{dx}\Rightarrow\mathrm{f}'\left(\mathrm{a}\right)=−\int_{\mathrm{0}} ^{\infty} \mathrm{cosx}\centerdot\mathrm{e}^{−\mathrm{a}\left(\mathrm{x}^{\mathrm{2}} +\mathrm{1}\right)} \mathrm{dx} \\ $$$$\mathrm{Let}\:\mathrm{p}=\int_{\mathrm{0}} ^{\infty} \mathrm{cosx}\centerdot\mathrm{e}^{−\mathrm{a}\left(\mathrm{x}^{\mathrm{2}} +\mathrm{1}\right)} \mathrm{dx}\:,\:\mathrm{q}=\int_{\mathrm{0}} ^{\infty} \mathrm{sinx}\centerdot\mathrm{e}^{−\mathrm{a}\left(\mathrm{x}^{\mathrm{2}} +\mathrm{1}\right)} \mathrm{dx} \\ $$$$\Rightarrow\mathrm{p}+\mathrm{qi}=\int_{\mathrm{0}} ^{\infty} \mathrm{e}^{\mathrm{xi}−\mathrm{a}\left(\mathrm{x}^{\mathrm{2}} +\mathrm{1}\right)} \mathrm{dx}=\int_{\mathrm{0}} ^{\infty} \mathrm{e}^{−\left(\mathrm{ax}^{\mathrm{2}} −\mathrm{xi}+\mathrm{a}\right)} \mathrm{dx} \\ $$$${What}\:{can}\:{we}\:{do}\:{next}\:? \\ $$
Commented by Aziztisffola last updated on 16/Jul/20
linearite of integral and use ∫_(−∞) ^(+∞) e^(−x^2 ) dx=(√π)
$$\mathrm{linearite}\:\mathrm{of}\:\mathrm{integral}\:\mathrm{and}\:\mathrm{use}\:\int_{−\infty} ^{+\infty} \mathrm{e}^{−\mathrm{x}^{\mathrm{2}} } \mathrm{dx}=\sqrt{\pi} \\ $$
Commented by abdomathmax last updated on 17/Jul/20
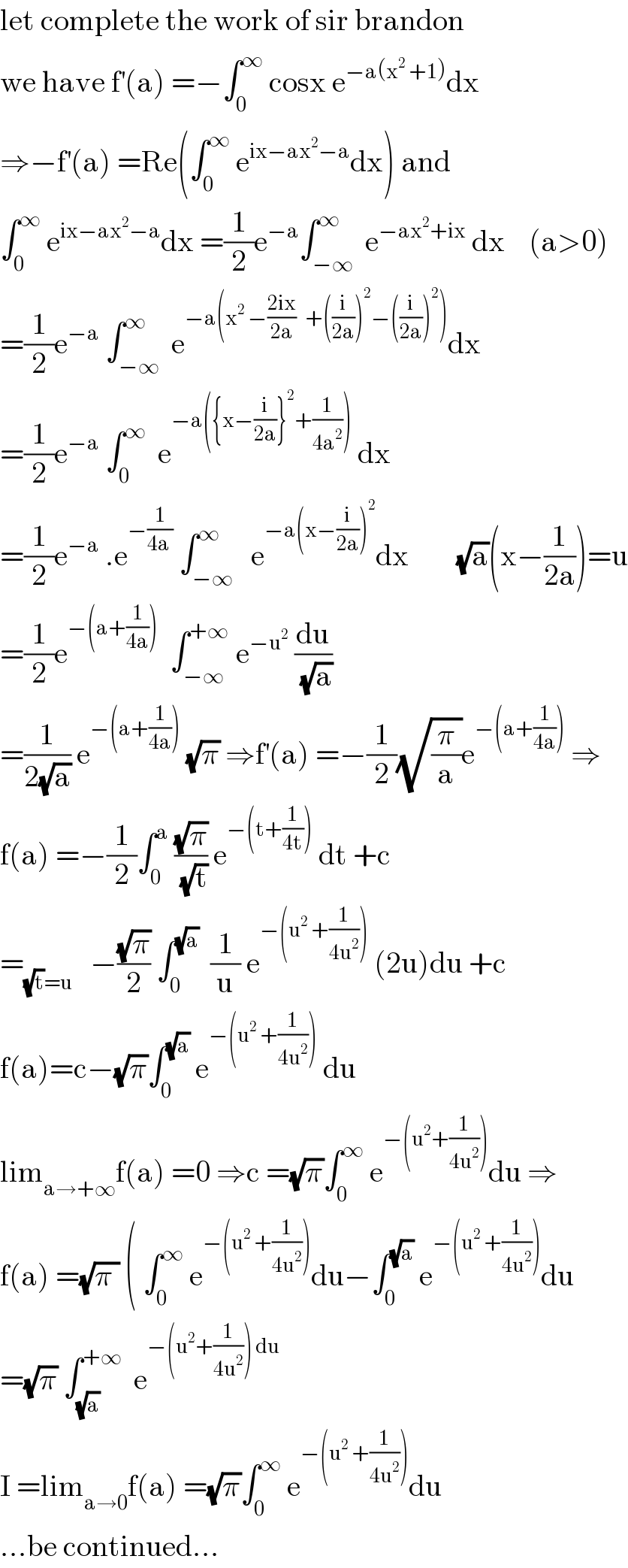
let complete the work of sir brandon we have f^′ (a) =−∫_0 ^∞ cosx e^(−a(x^2 +1)) dx ⇒−f^′ (a) =Re(∫_0 ^∞ e^(ix−ax^2 −a) dx) and ∫_0 ^∞ e^(ix−ax^2 −a) dx =(1/2)e^(−a) ∫_(−∞) ^∞ e^(−ax^2 +ix) dx (a>0) =(1/2)e^(−a) ∫_(−∞) ^∞ e^(−a(x^2 −((2ix)/(2a)) +((i/(2a)))^2 −((i/(2a)))^2 )) dx =(1/2)e^(−a) ∫_0 ^∞ e^(−a({x−(i/(2a))}^2 +(1/(4a^2 )))) dx =(1/2)e^(−a) .e^(−(1/(4a ))) ∫_(−∞) ^∞ e^(−a(x−(i/(2a)))^2 ) dx (√a)(x−(1/(2a)))=u =(1/2)e^(−(a+(1/(4a)))) ∫_(−∞) ^(+∞) e^(−u^2 ) (du/( (√a))) =(1/(2(√a))) e^(−(a+(1/(4a)))) (√π) ⇒f^′ (a) =−(1/2)(√(π/a))e^(−(a+(1/(4a)))) ⇒ f(a) =−(1/2)∫_0 ^a ((√π)/( (√t))) e^(−(t+(1/(4t)))) dt +c =_((√t)=u) −((√π)/2) ∫_0 ^(√a) (1/u) e^(−(u^2 +(1/(4u^2 )))) (2u)du +c f(a)=c−(√π)∫_0 ^(√a) e^(−(u^2 +(1/(4u^2 )))) du lim_(a→+∞) f(a) =0 ⇒c =(√π)∫_0 ^∞ e^(−(u^2 +(1/(4u^2 )))) du ⇒ f(a) =(√(π )) ( ∫_0 ^∞ e^(−(u^2 +(1/(4u^2 )))) du−∫_0 ^(√a) e^(−(u^2 +(1/(4u^2 )))) du =(√π) ∫_(√a) ^(+∞) e^(−(u^2 +(1/(4u^2 ))) du) I =lim_(a→0) f(a) =(√π)∫_0 ^∞ e^(−(u^2 +(1/(4u^2 )))) du ...be continued...
$$\mathrm{let}\:\mathrm{complete}\:\mathrm{the}\:\mathrm{work}\:\mathrm{of}\:\mathrm{sir}\:\mathrm{brandon} \\ $$$$\mathrm{we}\:\mathrm{have}\:\mathrm{f}^{'} \left(\mathrm{a}\right)\:=−\int_{\mathrm{0}} ^{\infty} \:\mathrm{cosx}\:\mathrm{e}^{−\mathrm{a}\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}\right)} \mathrm{dx} \\ $$$$\Rightarrow−\mathrm{f}^{'} \left(\mathrm{a}\right)\:=\mathrm{Re}\left(\int_{\mathrm{0}} ^{\infty} \:\mathrm{e}^{\mathrm{ix}−\mathrm{ax}^{\mathrm{2}} −\mathrm{a}} \mathrm{dx}\right)\:\mathrm{and} \\ $$$$\int_{\mathrm{0}} ^{\infty} \:\mathrm{e}^{\mathrm{ix}−\mathrm{ax}^{\mathrm{2}} −\mathrm{a}} \mathrm{dx}\:=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{e}^{−\mathrm{a}} \int_{−\infty} ^{\infty} \:\mathrm{e}^{−\mathrm{ax}^{\mathrm{2}} +\mathrm{ix}} \:\mathrm{dx}\:\:\:\:\left(\mathrm{a}>\mathrm{0}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{e}^{−\mathrm{a}} \:\int_{−\infty} ^{\infty} \:\mathrm{e}^{−\mathrm{a}\left(\mathrm{x}^{\mathrm{2}} \:−\frac{\mathrm{2ix}}{\mathrm{2a}}\:\:\:+\left(\frac{\mathrm{i}}{\mathrm{2a}}\right)^{\mathrm{2}} −\left(\frac{\mathrm{i}}{\mathrm{2a}}\right)^{\mathrm{2}} \right)} \mathrm{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{e}^{−\mathrm{a}} \:\int_{\mathrm{0}} ^{\infty} \:\:\mathrm{e}^{−\mathrm{a}\left(\left\{\mathrm{x}−\frac{\mathrm{i}}{\mathrm{2a}}\right\}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{4a}^{\mathrm{2}} }\right)} \:\mathrm{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{e}^{−\mathrm{a}} \:.\mathrm{e}^{−\frac{\mathrm{1}}{\mathrm{4a}\:}} \:\int_{−\infty} ^{\infty} \:\:\mathrm{e}^{−\mathrm{a}\left(\mathrm{x}−\frac{\mathrm{i}}{\mathrm{2a}}\right)^{\mathrm{2}} } \mathrm{dx}\:\:\:\:\:\:\:\:\sqrt{\mathrm{a}}\left(\mathrm{x}−\frac{\mathrm{1}}{\mathrm{2a}}\right)=\mathrm{u} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{e}^{−\left(\mathrm{a}+\frac{\mathrm{1}}{\mathrm{4a}}\right)} \:\:\int_{−\infty} ^{+\infty} \:\mathrm{e}^{−\mathrm{u}^{\mathrm{2}} } \:\frac{\mathrm{du}}{\:\sqrt{\mathrm{a}}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{a}}}\:\mathrm{e}^{−\left(\mathrm{a}+\frac{\mathrm{1}}{\mathrm{4a}}\right)} \:\sqrt{\pi}\:\Rightarrow\mathrm{f}^{'} \left(\mathrm{a}\right)\:=−\frac{\mathrm{1}}{\mathrm{2}}\sqrt{\frac{\pi}{\mathrm{a}}}\mathrm{e}^{−\left(\mathrm{a}+\frac{\mathrm{1}}{\mathrm{4a}}\right)} \:\Rightarrow \\ $$$$\mathrm{f}\left(\mathrm{a}\right)\:=−\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{a}} \:\frac{\sqrt{\pi}}{\:\sqrt{\mathrm{t}}}\:\mathrm{e}^{−\left(\mathrm{t}+\frac{\mathrm{1}}{\mathrm{4t}}\right)} \:\mathrm{dt}\:+\mathrm{c} \\ $$$$=_{\sqrt{\mathrm{t}}=\mathrm{u}} \:\:\:−\frac{\sqrt{\pi}}{\mathrm{2}}\:\int_{\mathrm{0}} ^{\sqrt{\mathrm{a}}} \:\:\frac{\mathrm{1}}{\mathrm{u}}\:\mathrm{e}^{−\left(\mathrm{u}^{\mathrm{2}} \:+\frac{\mathrm{1}}{\mathrm{4u}^{\mathrm{2}} }\right)} \:\left(\mathrm{2u}\right)\mathrm{du}\:+\mathrm{c} \\ $$$$\mathrm{f}\left(\mathrm{a}\right)=\mathrm{c}−\sqrt{\pi}\int_{\mathrm{0}} ^{\sqrt{\mathrm{a}}} \:\mathrm{e}^{−\left(\mathrm{u}^{\mathrm{2}} \:+\frac{\mathrm{1}}{\mathrm{4u}^{\mathrm{2}} }\right)} \:\mathrm{du} \\ $$$$\mathrm{lim}_{\mathrm{a}\rightarrow+\infty} \mathrm{f}\left(\mathrm{a}\right)\:=\mathrm{0}\:\Rightarrow\mathrm{c}\:=\sqrt{\pi}\int_{\mathrm{0}} ^{\infty} \:\mathrm{e}^{−\left(\mathrm{u}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{4u}^{\mathrm{2}} }\right)} \mathrm{du}\:\Rightarrow \\ $$$$\mathrm{f}\left(\mathrm{a}\right)\:=\sqrt{\pi\:}\:\left(\:\int_{\mathrm{0}} ^{\infty} \:\mathrm{e}^{−\left(\mathrm{u}^{\mathrm{2}} \:+\frac{\mathrm{1}}{\mathrm{4u}^{\mathrm{2}} }\right)} \mathrm{du}−\int_{\mathrm{0}} ^{\sqrt{\mathrm{a}}} \:\mathrm{e}^{−\left(\mathrm{u}^{\mathrm{2}} \:+\frac{\mathrm{1}}{\mathrm{4u}^{\mathrm{2}} }\right)} \mathrm{du}\right. \\ $$$$=\sqrt{\pi}\:\int_{\sqrt{\mathrm{a}}} ^{+\infty} \:\:\mathrm{e}^{−\left(\mathrm{u}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{4u}^{\mathrm{2}} }\right)\:\mathrm{du}} \\ $$$$\mathrm{I}\:=\mathrm{lim}_{\mathrm{a}\rightarrow\mathrm{0}} \mathrm{f}\left(\mathrm{a}\right)\:=\sqrt{\pi}\int_{\mathrm{0}} ^{\infty} \:\mathrm{e}^{−\left(\mathrm{u}^{\mathrm{2}} \:+\frac{\mathrm{1}}{\mathrm{4u}^{\mathrm{2}} }\right)} \mathrm{du} \\ $$$$…\mathrm{be}\:\mathrm{continued}… \\ $$
Answered by abdomathmax last updated on 16/Jul/20
this integral is solved at the platform? let A =∫_0 ^∞ ((cosx)/(x^2 +1))dx ⇒2A =∫_(−∞) ^(+∞) ((cosx)/(x^2 +1))dx =Re(∫_(−∞) ^(+∞) (e^(ix) /(x^2 +1))dx) let ϕ(z) =(e^(iz) /(z^2 +1)) we have lim_(z→+∞) ∣zϕ(z)∣ =0 and ϕ(z) =(e^(iz) /((z−i)(z+i))) residus tbeorem give ∫_(−∞) ^(+∞) ϕ(z)dz =2iπ Res(ϕ,i) =2iπ×(e^(−1) /(2i)) =(π/e) ⇒ 2A =(π/e) ⇒ A =(π/(2e))
$$\mathrm{this}\:\mathrm{integral}\:\mathrm{is}\:\mathrm{solved}\:\mathrm{at}\:\mathrm{the}\:\mathrm{platform}? \\ $$$$\mathrm{let}\:\mathrm{A}\:=\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{cosx}}{\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}}\mathrm{dx}\:\Rightarrow\mathrm{2A}\:=\int_{−\infty} ^{+\infty} \:\frac{\mathrm{cosx}}{\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}}\mathrm{dx} \\ $$$$=\mathrm{Re}\left(\int_{−\infty} ^{+\infty} \:\frac{\mathrm{e}^{\mathrm{ix}} }{\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}}\mathrm{dx}\right)\:\mathrm{let}\:\varphi\left(\mathrm{z}\right)\:=\frac{\mathrm{e}^{\mathrm{iz}} }{\mathrm{z}^{\mathrm{2}} +\mathrm{1}} \\ $$$$\mathrm{we}\:\mathrm{have}\:\mathrm{lim}_{\mathrm{z}\rightarrow+\infty} \mid\mathrm{z}\varphi\left(\mathrm{z}\right)\mid\:=\mathrm{0}\:\mathrm{and}\: \\ $$$$\varphi\left(\mathrm{z}\right)\:=\frac{\mathrm{e}^{\mathrm{iz}} }{\left(\mathrm{z}−\mathrm{i}\right)\left(\mathrm{z}+\mathrm{i}\right)}\:\mathrm{residus}\:\mathrm{tbeorem}\:\mathrm{give} \\ $$$$\int_{−\infty} ^{+\infty} \:\varphi\left(\mathrm{z}\right)\mathrm{dz}\:=\mathrm{2i}\pi\:\mathrm{Res}\left(\varphi,\mathrm{i}\right)\:=\mathrm{2i}\pi×\frac{\mathrm{e}^{−\mathrm{1}} }{\mathrm{2i}} \\ $$$$=\frac{\pi}{\mathrm{e}}\:\Rightarrow\:\mathrm{2A}\:=\frac{\pi}{\mathrm{e}}\:\Rightarrow\:\mathrm{A}\:=\frac{\pi}{\mathrm{2e}} \\ $$
Commented by Ar Brandon last updated on 17/Jul/20
Well-done Sir ����
Commented by Dwaipayan Shikari last updated on 17/Jul/20
Thanking all of you
$$\mathrm{Thanking}\:\mathrm{all}\:\mathrm{of}\:\mathrm{you} \\ $$
Commented by mathmax by abdo last updated on 17/Jul/20
you are welcome sir.
$$\mathrm{you}\:\mathrm{are}\:\mathrm{welcome}\:\mathrm{sir}. \\ $$
Commented by Dwaipayan Shikari last updated on 01/Aug/20
https://t.me/c/1457744274/126

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *