Question Number 42157 by Tawa1 last updated on 19/Aug/18
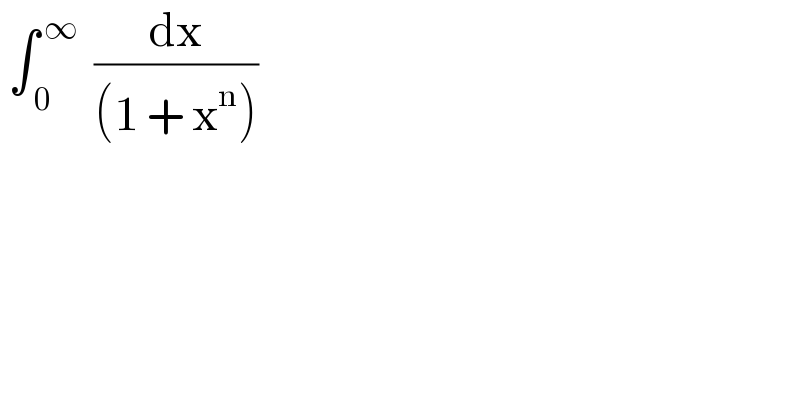
$$\:\int_{\:\mathrm{0}} ^{\:\infty} \:\:\frac{\mathrm{dx}}{\left(\mathrm{1}\:+\:\mathrm{x}^{\mathrm{n}} \right)} \\ $$
Commented by math khazana by abdo last updated on 19/Aug/18
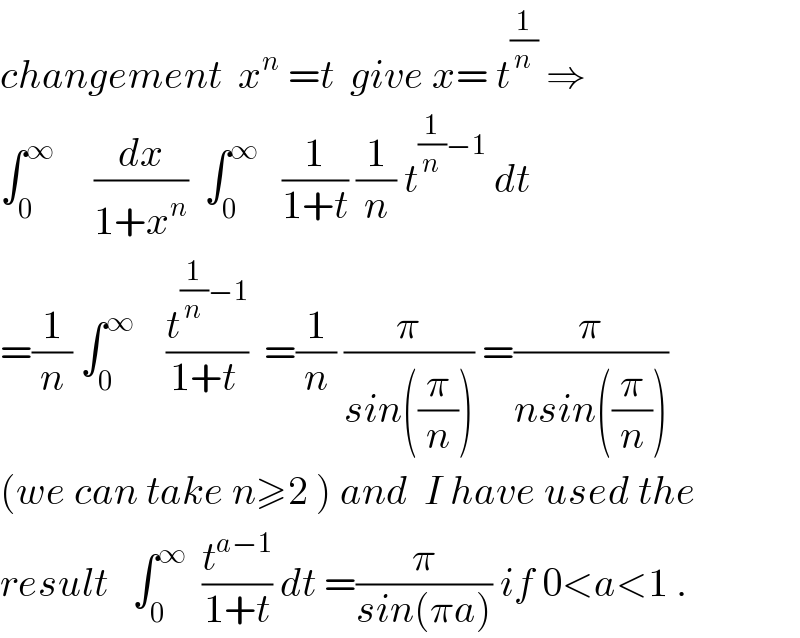
$${changement}\:\:{x}^{{n}} \:={t}\:\:{give}\:{x}=\:{t}^{\frac{\mathrm{1}}{{n}}} \:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\infty} \:\:\:\:\:\frac{{dx}}{\mathrm{1}+{x}^{{n}} }\:\:\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{\mathrm{1}}{\mathrm{1}+{t}}\:\frac{\mathrm{1}}{{n}}\:{t}^{\frac{\mathrm{1}}{{n}}−\mathrm{1}} \:{dt} \\ $$$$=\frac{\mathrm{1}}{{n}}\:\int_{\mathrm{0}} ^{\infty} \:\:\:\:\frac{{t}^{\frac{\mathrm{1}}{{n}}−\mathrm{1}} }{\mathrm{1}+{t}\:}\:\:=\frac{\mathrm{1}}{{n}}\:\frac{\pi}{{sin}\left(\frac{\pi}{{n}}\right)}\:=\frac{\pi}{{nsin}\left(\frac{\pi}{{n}}\right)} \\ $$$$\left({we}\:{can}\:{take}\:{n}\geqslant\mathrm{2}\:\right)\:{and}\:\:{I}\:{have}\:{used}\:{the} \\ $$$${result}\:\:\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{{t}^{{a}−\mathrm{1}} }{\mathrm{1}+{t}}\:{dt}\:=\frac{\pi}{{sin}\left(\pi{a}\right)}\:{if}\:\mathrm{0}<{a}<\mathrm{1}\:. \\ $$
Commented by Tawa1 last updated on 19/Aug/18

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
Commented by math khazana by abdo last updated on 20/Aug/18

$${thanks}\:{sir}. \\ $$
