Question Number 17034 by arnabpapu550@gmail.com last updated on 30/Jun/17
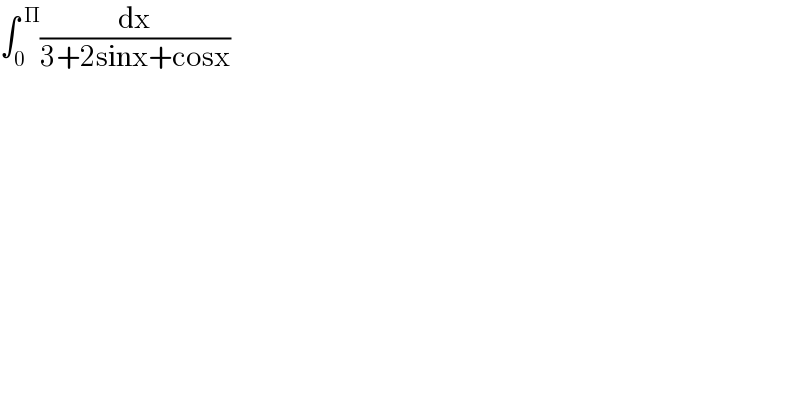
$$\int_{\mathrm{0}} ^{\:\Pi} \frac{\mathrm{dx}}{\mathrm{3}+\mathrm{2sinx}+\mathrm{cosx}} \\ $$
Answered by Arnab Maiti last updated on 03/Jul/17
![=∫_0 ^( Π) (dx/(3+2×((2tan(x/2))/(1+tan^2 (x/2)))+((1−tan^2 (x/2))/(1+tan^2 (x/2))))) =∫_0 ^( Π) ((sec^2 (x/2)dx)/(3(1+tan^2 (x/2))+4tan(x/2)+1−tan^2 (x/2))) put tan(x/2)=z⇒(1/2)sec^2 (x/2)dx=dz =∫_0 ^( ∞) ((2dz)/(2z^2 +4z+4)) =∫_0 ^∞ (dz/(z^2 +2z+2))=∫_0 ^∞ (dz/(z^2 +2×1×z+1^2 +1)) =∫_0 ^∞ (dz/((z+1)^2 +1)) =[tan^(−1) (z+1)]_0 ^∞ =[tan^(−1) (∞)−tan^(−1) (1)] =(Π/2)−(Π/4)=(Π/4)](https://www.tinkutara.com/question/Q17267.png)
$$=\int_{\mathrm{0}} ^{\:\Pi} \frac{\mathrm{dx}}{\mathrm{3}+\mathrm{2}×\frac{\mathrm{2tan}\frac{\mathrm{x}}{\mathrm{2}}}{\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \frac{\mathrm{x}}{\mathrm{2}}}+\frac{\mathrm{1}−\mathrm{tan}^{\mathrm{2}} \frac{\mathrm{x}}{\mathrm{2}}}{\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \frac{\mathrm{x}}{\mathrm{2}}}} \\ $$$$=\int_{\mathrm{0}} ^{\:\Pi} \frac{\mathrm{sec}^{\mathrm{2}} \frac{\mathrm{x}}{\mathrm{2}}\mathrm{dx}}{\mathrm{3}\left(\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \frac{\mathrm{x}}{\mathrm{2}}\right)+\mathrm{4tan}\frac{\mathrm{x}}{\mathrm{2}}+\mathrm{1}−\mathrm{tan}^{\mathrm{2}} \frac{\mathrm{x}}{\mathrm{2}}} \\ $$$$\:\mathrm{put}\:\mathrm{tan}\frac{\mathrm{x}}{\mathrm{2}}=\mathrm{z}\Rightarrow\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sec}^{\mathrm{2}} \frac{\mathrm{x}}{\mathrm{2}}\mathrm{dx}=\mathrm{dz} \\ $$$$=\int_{\mathrm{0}} ^{\:\infty} \frac{\mathrm{2dz}}{\mathrm{2z}^{\mathrm{2}} +\mathrm{4z}+\mathrm{4}} \\ $$$$=\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{dz}}{\mathrm{z}^{\mathrm{2}} +\mathrm{2z}+\mathrm{2}}=\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{dz}}{\mathrm{z}^{\mathrm{2}} +\mathrm{2}×\mathrm{1}×\mathrm{z}+\mathrm{1}^{\mathrm{2}} +\mathrm{1}} \\ $$$$=\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{dz}}{\left(\mathrm{z}+\mathrm{1}\right)^{\mathrm{2}} +\mathrm{1}} \\ $$$$=\left[\mathrm{tan}^{−\mathrm{1}} \left(\mathrm{z}+\mathrm{1}\right)\right]_{\mathrm{0}} ^{\infty} =\left[\mathrm{tan}^{−\mathrm{1}} \left(\infty\right)−\mathrm{tan}^{−\mathrm{1}} \left(\mathrm{1}\right)\right] \\ $$$$=\frac{\Pi}{\mathrm{2}}−\frac{\Pi}{\mathrm{4}}=\frac{\Pi}{\mathrm{4}} \\ $$
