0-dx-4-x-2-

Question Number 50659 by rahul 19 last updated on 18/Dec/18

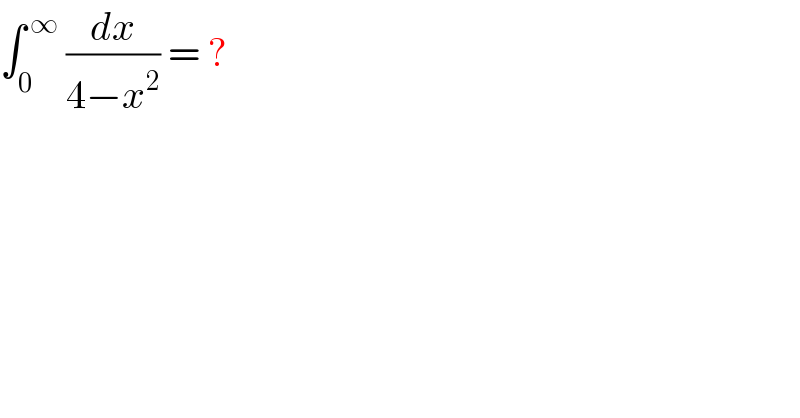
$$\int_{\mathrm{0}\:} ^{\:\infty} \:\frac{{dx}}{\mathrm{4}−{x}^{\mathrm{2}} }\:=\:? \\ $$

Commented by maxmathsup by imad last updated on 18/Dec/18

this integral diverges let prove this let A_n =∫_0 ^(2+(1/n)) (dx/(4−x^2 )) we have ∫_0 ^2 (dx/(4−x^2 )) =lim_(n→+∞) A_n but A_n = (1/4) ∫_0 ^(2+(1/n)) ( (1/(2−x)) +(1/(2+x)))dx =(1/4)[ln∣((2+x)/(2−x))∣]_0 ^(2+(1/n)) = (1/4){ln∣ ((4+(1/n))/(−(1/n)))∣} =(1/4)ln(4n+1) ⇒lim_(n→+∞) A_n =+∞

$${this}\:{integral}\:{diverges}\:{let}\:{prove}\:{this}\:\:{let}\:{A}_{{n}} =\int_{\mathrm{0}} ^{\mathrm{2}+\frac{\mathrm{1}}{{n}}} \:\:\:\frac{{dx}}{\mathrm{4}−{x}^{\mathrm{2}} } \\ $$$${we}\:{have}\:\int_{\mathrm{0}} ^{\mathrm{2}} \:\:\:\frac{{dx}}{\mathrm{4}−{x}^{\mathrm{2}} }\:={lim}_{{n}\rightarrow+\infty} \:{A}_{{n}} \:\:\:{but} \\ $$$${A}_{{n}} =\:\frac{\mathrm{1}}{\mathrm{4}}\:\int_{\mathrm{0}} ^{\mathrm{2}+\frac{\mathrm{1}}{{n}}} \:\:\left(\:\frac{\mathrm{1}}{\mathrm{2}−{x}}\:+\frac{\mathrm{1}}{\mathrm{2}+{x}}\right){dx}\:=\frac{\mathrm{1}}{\mathrm{4}}\left[{ln}\mid\frac{\mathrm{2}+{x}}{\mathrm{2}−{x}}\mid\right]_{\mathrm{0}} ^{\mathrm{2}+\frac{\mathrm{1}}{{n}}} \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{4}}\left\{{ln}\mid\:\frac{\mathrm{4}+\frac{\mathrm{1}}{{n}}}{−\frac{\mathrm{1}}{{n}}}\mid\right\}\:=\frac{\mathrm{1}}{\mathrm{4}}{ln}\left(\mathrm{4}{n}+\mathrm{1}\right)\:\Rightarrow{lim}_{{n}\rightarrow+\infty} \:\:\:{A}_{{n}} =+\infty \\ $$

Commented by mr W last updated on 18/Dec/18

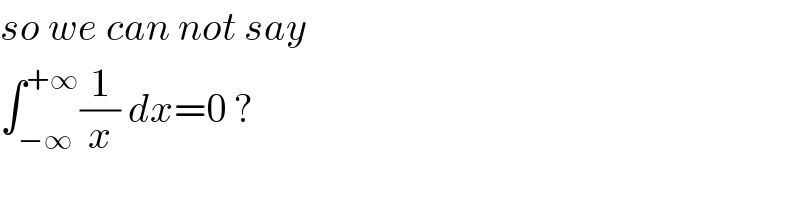
so we can not say ∫_(−∞) ^(+∞) (1/x) dx=0 ?

$${so}\:{we}\:{can}\:{not}\:{say} \\ $$$$\int_{−\infty} ^{+\infty} \frac{\mathrm{1}}{{x}}\:{dx}=\mathrm{0}\:? \\ $$

Commented by maxmathsup by imad last updated on 18/Dec/18

this integral is another type because x→(1/x) is odd.

$${this}\:{integral}\:{is}\:{another}\:{type}\:{because}\:{x}\rightarrow\frac{\mathrm{1}}{{x}}\:{is}\:{odd}. \\ $$

Commented by maxmathsup by imad last updated on 18/Dec/18

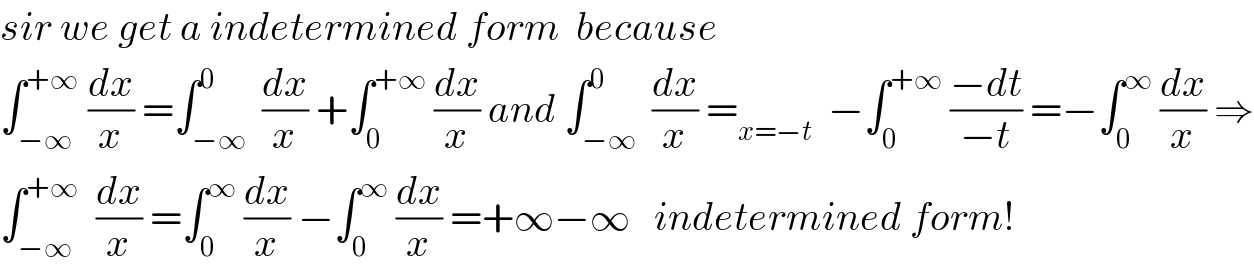
sir we get a indetermined form because ∫_(−∞) ^(+∞) (dx/x) =∫_(−∞) ^0 (dx/x) +∫_0 ^(+∞) (dx/x) and ∫_(−∞) ^0 (dx/x) =_(x=−t) −∫_0 ^(+∞) ((−dt)/(−t)) =−∫_0 ^∞ (dx/x) ⇒ ∫_(−∞) ^(+∞) (dx/x) =∫_0 ^∞ (dx/x) −∫_0 ^∞ (dx/x) =+∞−∞ indetermined form!

$${sir}\:{we}\:{get}\:{a}\:{indetermined}\:{form}\:\:{because} \\ $$$$\int_{−\infty} ^{+\infty} \:\frac{{dx}}{{x}}\:=\int_{−\infty} ^{\mathrm{0}} \:\frac{{dx}}{{x}}\:+\int_{\mathrm{0}} ^{+\infty} \:\frac{{dx}}{{x}}\:{and}\:\int_{−\infty} ^{\mathrm{0}} \:\frac{{dx}}{{x}}\:=_{{x}=−{t}} \:\:−\int_{\mathrm{0}} ^{+\infty} \:\frac{−{dt}}{−{t}}\:=−\int_{\mathrm{0}} ^{\infty} \:\frac{{dx}}{{x}}\:\Rightarrow \\ $$$$\int_{−\infty} ^{+\infty} \:\:\frac{{dx}}{{x}}\:=\int_{\mathrm{0}} ^{\infty} \:\frac{{dx}}{{x}}\:−\int_{\mathrm{0}} ^{\infty} \:\frac{{dx}}{{x}}\:=+\infty−\infty\:\:\:{indetermined}\:{form}! \\ $$

Answered by mr W last updated on 18/Dec/18

∫_(0 ) ^( ∞) (dx/(2^2 −x^2 )) =(1/4)[ln ∣((2+x)/(2−x))∣]_0 ^2 +(1/4)[ln ∣((2+x)/(2−x))∣]_2 ^∞ =(1/4)(A)+(1/4)(−A) =0

$$\int_{\mathrm{0}\:} ^{\:\infty} \:\frac{{dx}}{\mathrm{2}^{\mathrm{2}} −{x}^{\mathrm{2}} }\: \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\left[\mathrm{ln}\:\mid\frac{\mathrm{2}+{x}}{\mathrm{2}−{x}}\mid\right]_{\mathrm{0}} ^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{4}}\left[\mathrm{ln}\:\mid\frac{\mathrm{2}+{x}}{\mathrm{2}−{x}}\mid\right]_{\mathrm{2}} ^{\infty} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\left({A}\right)+\frac{\mathrm{1}}{\mathrm{4}}\left(−{A}\right) \\ $$$$=\mathrm{0} \\ $$

Commented by rahul 19 last updated on 18/Dec/18

thanks sir!

Commented by mr W last updated on 18/Dec/18

i am not sure if the answer is correct, since A→∞. we can not say ∞−∞=0.

$${i}\:{am}\:{not}\:{sure}\:{if}\:{the}\:{answer}\:{is}\:{correct}, \\ $$$${since}\:{A}\rightarrow\infty.\:{we}\:{can}\:{not}\:{say}\:\infty−\infty=\mathrm{0}. \\ $$

Commented by afachri last updated on 18/Dec/18

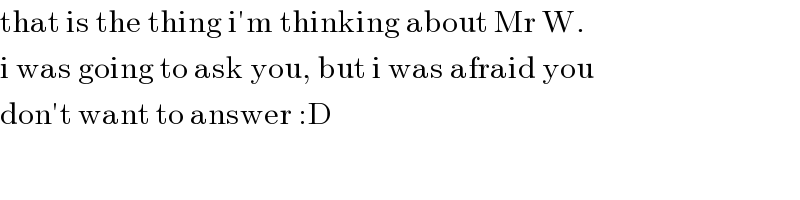
that is the thing i′m thinking about Mr W. i was going to ask you, but i was afraid you don′t want to answer :D

$$\mathrm{that}\:\mathrm{is}\:\mathrm{the}\:\mathrm{thing}\:\mathrm{i}'\mathrm{m}\:\mathrm{thinking}\:\mathrm{about}\:\mathrm{Mr}\:\mathrm{W}. \\ $$$$\mathrm{i}\:\mathrm{was}\:\mathrm{going}\:\mathrm{to}\:\mathrm{ask}\:\mathrm{you},\:\mathrm{but}\:\mathrm{i}\:\mathrm{was}\:\mathrm{afraid}\:\mathrm{you} \\ $$$$\mathrm{don}'\mathrm{t}\:\mathrm{want}\:\mathrm{to}\:\mathrm{answer}\::\mathrm{D} \\ $$

Answered by MJS last updated on 18/Dec/18

∫(dx/(4−x^2 ))=(1/4)(ln ∣x+2∣ −ln ∣x−2∣) +C this is not defined for x=±2 Cauchy Principal Value: ∫_0 ^∞ (dx/(4−x^2 ))=lim_(δ→0) (∫_0 ^(2−δ) (dx/(4−x^2 ))+∫_(2+δ) ^∞ (dx/(4−x^2 )))= =lim_(δ→0) ((1/4)((ln ∣4−δ∣ −ln ∣−δ∣)−(ln ∣2∣ −ln ∣−2∣)+ +(lim_(x→∞) (ln ∣x+2∣ −ln ∣x−2∣)−(ln ∣4+δ∣ −ln ∣δ∣)=0 (as one can easily see)

$$\int\frac{{dx}}{\mathrm{4}−{x}^{\mathrm{2}} }=\frac{\mathrm{1}}{\mathrm{4}}\left(\mathrm{ln}\:\mid{x}+\mathrm{2}\mid\:−\mathrm{ln}\:\mid{x}−\mathrm{2}\mid\right)\:+{C} \\ $$$$\mathrm{this}\:\mathrm{is}\:\mathrm{not}\:\mathrm{defined}\:\mathrm{for}\:{x}=\pm\mathrm{2} \\ $$$$\mathrm{Cauchy}\:\mathrm{Principal}\:\mathrm{Value}: \\ $$$$\underset{\mathrm{0}} {\overset{\infty} {\int}}\frac{{dx}}{\mathrm{4}−{x}^{\mathrm{2}} }=\underset{\delta\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\underset{\mathrm{0}} {\overset{\mathrm{2}−\delta} {\int}}\frac{{dx}}{\mathrm{4}−{x}^{\mathrm{2}} }+\underset{\mathrm{2}+\delta} {\overset{\infty} {\int}}\frac{{dx}}{\mathrm{4}−{x}^{\mathrm{2}} }\right)= \\ $$$$=\underset{\delta\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\frac{\mathrm{1}}{\mathrm{4}}\left(\left(\mathrm{ln}\:\mid\mathrm{4}−\delta\mid\:−\mathrm{ln}\:\mid−\delta\mid\right)−\left(\mathrm{ln}\:\mid\mathrm{2}\mid\:−\mathrm{ln}\:\mid−\mathrm{2}\mid\right)+\right.\right. \\ $$$$\:\:\:\:\:+\left(\underset{{x}\rightarrow\infty} {\mathrm{lim}}\left(\mathrm{ln}\:\mid{x}+\mathrm{2}\mid\:−\mathrm{ln}\:\mid{x}−\mathrm{2}\mid\right)−\left(\mathrm{ln}\:\mid\mathrm{4}+\delta\mid\:−\mathrm{ln}\:\mid\delta\mid\right)=\mathrm{0}\right. \\ $$$$\left(\mathrm{as}\:\mathrm{one}\:\mathrm{can}\:\mathrm{easily}\:\mathrm{see}\right) \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply