Question Number 85676 by john santu last updated on 24/Mar/20
![∫ _0 ^∞ (dx/((x+(√(1+x^2 )))^2 )) let x = tan t ⇒dx=sec^2 t dt ∫_0 ^(π/2) ((sec^2 t dt)/((tan t+sec t)^2 )) = ∫_0 ^(π/2) (dt/((sin t+1)^2 )) = ∫_0 ^(π/2) (dt/((cos (1/2)t+sin (1/2)t)^4 )) = ∫_0 ^(π/2) (dt/(4cos^4 ((1/2)t−(π/4)))) = (1/4)∫_0 ^(π/2) sec^4 ((1/2)t−(π/4)) dt [ let (1/2)t−(π/4)= u] = (1/4)∫_(−(π/4)) ^0 sec^4 u ×2du =(1/2)∫ _(−(π/4)) ^0 (tan^2 u+1) d(tan u) = (1/2) [(1/3)tan^3 u + tan u ]_(−(π/4)) ^0 = (1/2) [ 0−(−(1/3)−1)]= (2/3)](https://www.tinkutara.com/question/Q85676.png)
Commented by jagoll last updated on 24/Mar/20
![i try by Euler substitution let (√(1+x^2 )) = x+t 1+x^2 = x^2 +2xt+t^2 2xt+t^2 =1 ⇒ x = ((1−t^2 )/(2t)) dx = ((−t^2 −1)/(2t^2 )) dt ∫ (1/((((1−t^2 )/(2t))+((1+t^2 )/(2t)))^2 )) × (((−t^2 −1)/(2t^2 ))) dt ∫ (t^2 /(2t^2 )) ×(−t^2 −1) dt = −(1/2)∫ (t^2 +1)dt −(1/2) [(1/3)t^3 +t ] =−(1/6)t [t^2 +3 ] −(1/6) ((√(1+x^2 )) −x ) (2x^2 +4−2x(√(1+x^2 )) ) lim_(x→∞) −(1/6)((√(1+x^2 ))−x)(2x^2 +4−2x(√(1+x^2 ))) +(4/6) = (2/3)](https://www.tinkutara.com/question/Q85680.png)
Commented by john santu last updated on 24/Mar/20

Commented by sakeefhasan05@gmail.com last updated on 24/Mar/20
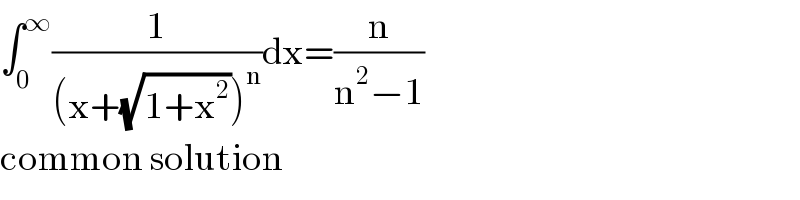
Commented by sakeefhasan05@gmail.com last updated on 24/Mar/20

Commented by john santu last updated on 24/Mar/20

Commented by sakeefhasan05@gmail.com last updated on 24/Mar/20
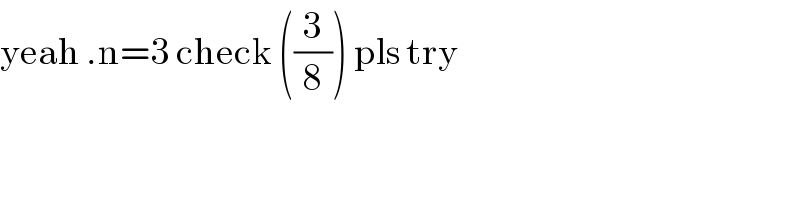
Commented by jagoll last updated on 24/Mar/20

Commented by sakeefhasan05@gmail.com last updated on 24/Mar/20
![sry (n/((n^2 −1))) ,[n^2 −1≠0] so (n≠1) & (n≠−1)](https://www.tinkutara.com/question/Q85726.png)
Commented by sakeefhasan05@gmail.com last updated on 24/Mar/20
Commented by mathmax by abdo last updated on 24/Mar/20
![let A_n =∫_0 ^∞ (dx/((x+(√(1+x^2 )))^n )) we do the changement x=sh(t) ⇒ A_n =∫_0 ^∞ ((ch(t))/((sh(t)+ch(t))^n ))dt =∫_0 ^∞ ((ch(t))/((((e^t −e^(−t) )/2)+((e^t +e^(−t) )/2))^n ))dt =∫_0 ^∞ e^(−nt) (((e^t +e^(−t) )/2))dt =(1/2) ∫_0 ^∞ ( e^((−n+1)t) +e^(−(n+1)t) )dt =(1/2)[(1/(1−n))e^((1−n)t) −(1/(n+1))e^(−(n+1)t) ]_0 ^(+∞) =(1/2){−(1/(1−n))+(1/(n+1))} =(1/2)((1/(n+1))+(1/(n−1))) =(1/2)(((2n)/(n^2 −1))) ⇒ A_n =(n/(n^2 −1)) (n>1) so ∫_0 ^∞ (dx/((x+(√(1+x^2 )))^2 )) =(2/(2^2 −1)) =(2/3)](https://www.tinkutara.com/question/Q85731.png)
Commented by john santu last updated on 24/Mar/20
Commented by john santu last updated on 24/Mar/20

Commented by mathmax by abdo last updated on 24/Mar/20
Commented by mathmax by abdo last updated on 24/Mar/20

Commented by john santu last updated on 25/Mar/20

