Menu Close

0-e-ix-2-dx-plz-

Tinku Tara 0 Comments
Pin




Question Number 45841 by Rauny last updated on 17/Oct/18
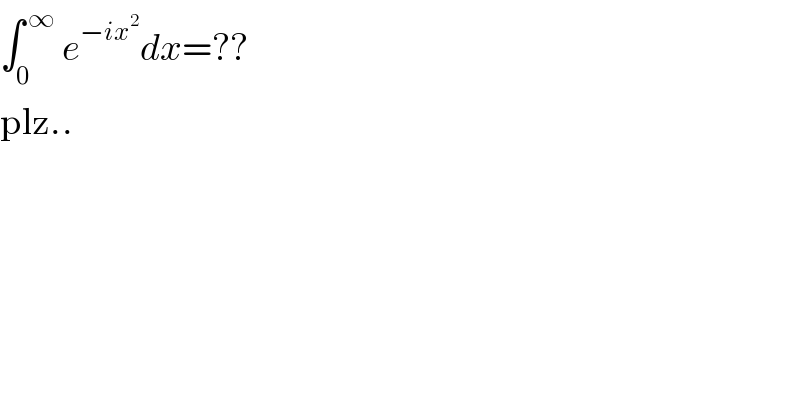
∫_0 ^( ∞) e^(−ix^2 ) dx=?? plz..
$$\int_{\mathrm{0}} ^{\:\infty} \:{e}^{−{ix}^{\mathrm{2}} } {dx}=?? \\ $$$$\mathrm{plz}.. \\ $$
Commented by MJS last updated on 17/Oct/18
((√((2π)))/4)−((√((2π)))/4)i
$$\frac{\sqrt{\left(\mathrm{2}\pi\right)}}{\mathrm{4}}−\frac{\sqrt{\left(\mathrm{2}\pi\right)}}{\mathrm{4}}\mathrm{i} \\ $$
Commented by maxmathsup by imad last updated on 17/Oct/18
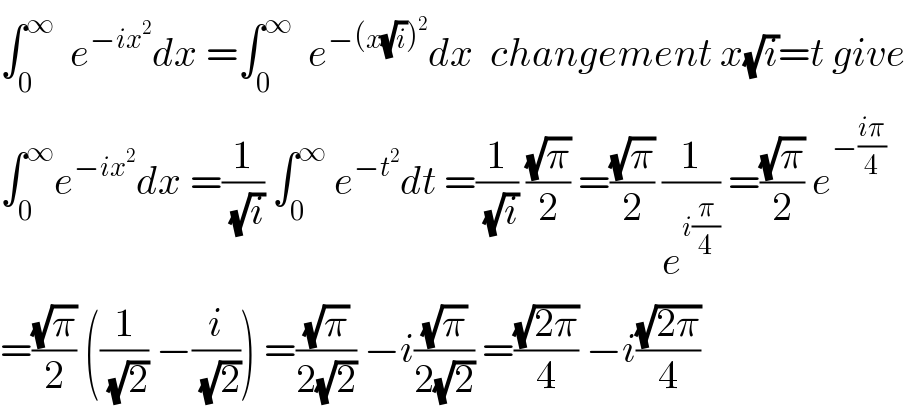
∫_0 ^∞ e^(−ix^2 ) dx =∫_0 ^∞ e^(−(x(√i))^2 ) dx changement x(√i)=t give ∫_0 ^∞ e^(−ix^2 ) dx =(1/( (√i))) ∫_0 ^∞ e^(−t^2 ) dt =(1/( (√i))) ((√π)/2) =((√π)/2) (1/e^(i(π/4)) ) =((√π)/2) e^(−((iπ)/4)) =((√π)/2) ((1/( (√2))) −(i/( (√2)))) =((√π)/(2(√2))) −i((√π)/(2(√2))) =((√(2π))/4) −i((√(2π))/4)
$$\int_{\mathrm{0}} ^{\infty} \:\:{e}^{−{ix}^{\mathrm{2}} } {dx}\:=\int_{\mathrm{0}} ^{\infty} \:\:{e}^{−\left({x}\sqrt{{i}}\right)^{\mathrm{2}} } {dx}\:\:{changement}\:{x}\sqrt{{i}}={t}\:{give} \\ $$$$\int_{\mathrm{0}} ^{\infty} {e}^{−{ix}^{\mathrm{2}} } {dx}\:=\frac{\mathrm{1}}{\:\sqrt{{i}}}\:\int_{\mathrm{0}} ^{\infty} \:{e}^{−{t}^{\mathrm{2}} } {dt}\:=\frac{\mathrm{1}}{\:\sqrt{{i}}}\:\frac{\sqrt{\pi}}{\mathrm{2}}\:=\frac{\sqrt{\pi}}{\mathrm{2}}\:\frac{\mathrm{1}}{{e}^{{i}\frac{\pi}{\mathrm{4}}} }\:=\frac{\sqrt{\pi}}{\mathrm{2}}\:{e}^{−\frac{{i}\pi}{\mathrm{4}}} \\ $$$$=\frac{\sqrt{\pi}}{\mathrm{2}}\:\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\:−\frac{{i}}{\:\sqrt{\mathrm{2}}}\right)\:=\frac{\sqrt{\pi}}{\mathrm{2}\sqrt{\mathrm{2}}}\:−{i}\frac{\sqrt{\pi}}{\mathrm{2}\sqrt{\mathrm{2}}}\:=\frac{\sqrt{\mathrm{2}\pi}}{\mathrm{4}}\:−{i}\frac{\sqrt{\mathrm{2}\pi}}{\mathrm{4}} \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 17/Oct/18
t=ix^2 dt=2ixdx dx=(dt/(2ix))=(dt/(2i×(√t)))×(√i) ∫_0 ^∞ e^(−t) ×t^(−(1/2)) ×(1/(2(√i))) (1/(2(√i)))∫_0 ^∞ e^(−t) ×t^((1/2)−1) dt ←gamma function (1/(2(√i)))×⌈((1/2)) (1/(2(√i)))×(√π) {since ⌈((1/2))=(√π) } =(1/2)×(((√i) )/i)×(√π) now calculation of (√i) =(1/( (√)2))×(√(1−1+2i)) =(1/( (√2)))×(√(1^2 +i^2 +2×i×1)) =(1/( (√2)))×(√((1+i)^2 )) =(1/( (√2)))×(1+i) so the ans is =(1/2)×(1/( (√2) ))×((1+i)/i)×(√π) =(1/(2(√2) ))×(1+(1/i))×(√π) =(1/(2(√2)))×(1−i)×(√π) {∫_0 ^∞ e^(−y) ×y^(n−1) dy=⌈(n)}
$${t}={ix}^{\mathrm{2}} \:{dt}=\mathrm{2}{ixdx} \\ $$$${dx}=\frac{{dt}}{\mathrm{2}{ix}}=\frac{{dt}}{\mathrm{2}{i}×\sqrt{{t}}}×\sqrt{{i}} \\ $$$$\int_{\mathrm{0}} ^{\infty} {e}^{−{t}} ×{t}^{−\frac{\mathrm{1}}{\mathrm{2}}} ×\frac{\mathrm{1}}{\mathrm{2}\sqrt{{i}}} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}\sqrt{{i}}}\int_{\mathrm{0}} ^{\infty} {e}^{−{t}} ×{t}^{\frac{\mathrm{1}}{\mathrm{2}}−\mathrm{1}} {dt}\:\:\leftarrow{gamma}\:{function} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}\sqrt{{i}}}×\lceil\left(\frac{\mathrm{1}}{\mathrm{2}}\right) \\ $$$$\frac{\mathrm{1}}{\mathrm{2}\sqrt{{i}}}×\sqrt{\pi}\:\:\:\:\:\:\:\:\left\{{since}\:\lceil\left(\frac{\mathrm{1}}{\mathrm{2}}\right)=\sqrt{\pi}\:\right\} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}×\frac{\sqrt{{i}}\:}{{i}}×\sqrt{\pi}\: \\ $$$${now}\:{calculation}\:{of}\:\sqrt{{i}}\: \\ $$$$=\frac{\mathrm{1}}{\:\sqrt{}\mathrm{2}}×\sqrt{\mathrm{1}−\mathrm{1}+\mathrm{2}{i}}\: \\ $$$$=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}×\sqrt{\mathrm{1}^{\mathrm{2}} +{i}^{\mathrm{2}} +\mathrm{2}×{i}×\mathrm{1}}\: \\ $$$$=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}×\sqrt{\left(\mathrm{1}+{i}\right)^{\mathrm{2}} }\: \\ $$$$=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}×\left(\mathrm{1}+{i}\right) \\ $$$${so}\:{the}\:{ans}\:{is} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}×\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}\:}×\frac{\mathrm{1}+{i}}{{i}}×\sqrt{\pi}\: \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}\:}×\left(\mathrm{1}+\frac{\mathrm{1}}{{i}}\right)×\sqrt{\pi}\: \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}×\left(\mathrm{1}−{i}\right)×\sqrt{\pi}\: \\ $$$$ \\ $$$$\left\{\int_{\mathrm{0}} ^{\infty} {e}^{−{y}} ×{y}^{{n}−\mathrm{1}} {dy}=\lceil\left({n}\right)\right\} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *