Question Number 128982 by bramlexs22 last updated on 11/Jan/21

$$\:\int_{\:\mathrm{0}} ^{\:\infty} \:\mathrm{e}^{−\mathrm{x}^{\mathrm{2}} } \:\mathrm{cos}\:\mathrm{x}\:\mathrm{dx} \\ $$
Answered by mathmax by abdo last updated on 12/Jan/21
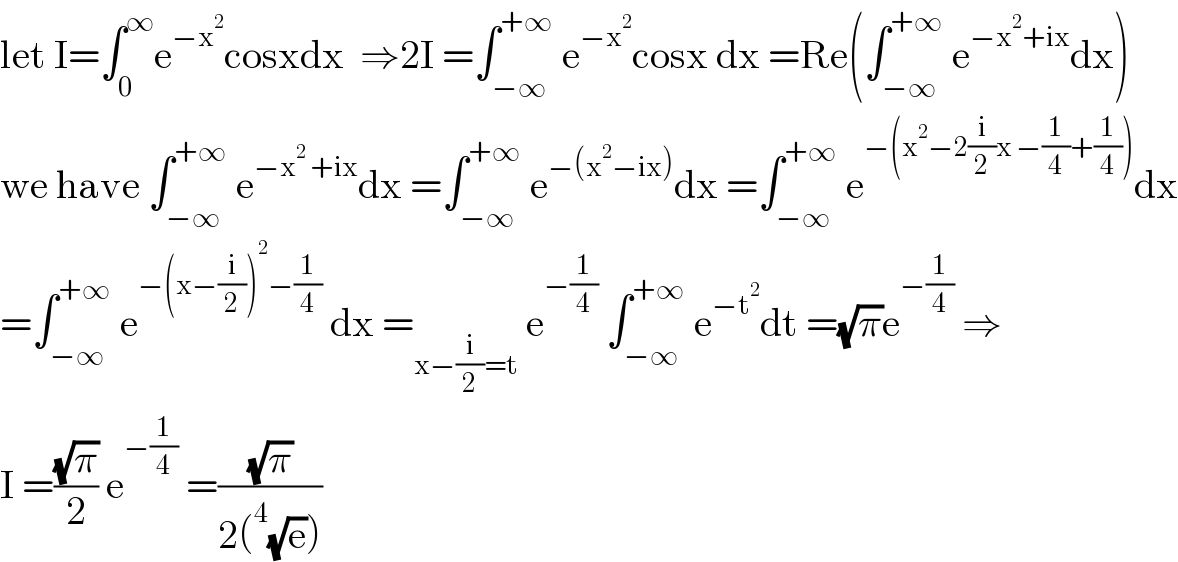
$$\mathrm{let}\:\mathrm{I}=\int_{\mathrm{0}} ^{\infty} \mathrm{e}^{−\mathrm{x}^{\mathrm{2}} } \mathrm{cosxdx}\:\:\Rightarrow\mathrm{2I}\:=\int_{−\infty} ^{+\infty} \:\mathrm{e}^{−\mathrm{x}^{\mathrm{2}} } \mathrm{cosx}\:\mathrm{dx}\:=\mathrm{Re}\left(\int_{−\infty} ^{+\infty} \:\mathrm{e}^{−\mathrm{x}^{\mathrm{2}} +\mathrm{ix}} \mathrm{dx}\right) \\ $$$$\mathrm{we}\:\mathrm{have}\:\int_{−\infty} ^{+\infty} \:\mathrm{e}^{−\mathrm{x}^{\mathrm{2}} \:+\mathrm{ix}} \mathrm{dx}\:=\int_{−\infty} ^{+\infty} \:\mathrm{e}^{−\left(\mathrm{x}^{\mathrm{2}} −\mathrm{ix}\right)} \mathrm{dx}\:=\int_{−\infty} ^{+\infty} \:\mathrm{e}^{−\left(\mathrm{x}^{\mathrm{2}} −\mathrm{2}\frac{\mathrm{i}}{\mathrm{2}}\mathrm{x}\:−\frac{\mathrm{1}}{\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{4}}\right)} \mathrm{dx} \\ $$$$=\int_{−\infty} ^{+\infty} \:\mathrm{e}^{−\left(\mathrm{x}−\frac{\mathrm{i}}{\mathrm{2}}\right)^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{4}}} \:\mathrm{dx}\:=_{\mathrm{x}−\frac{\mathrm{i}}{\mathrm{2}}=\mathrm{t}} \:\mathrm{e}^{−\frac{\mathrm{1}}{\mathrm{4}}} \:\int_{−\infty} ^{+\infty} \:\mathrm{e}^{−\mathrm{t}^{\mathrm{2}} } \mathrm{dt}\:=\sqrt{\pi}\mathrm{e}^{−\frac{\mathrm{1}}{\mathrm{4}}} \:\Rightarrow \\ $$$$\mathrm{I}\:=\frac{\sqrt{\pi}}{\mathrm{2}}\:\mathrm{e}^{−\frac{\mathrm{1}}{\mathrm{4}}} \:=\frac{\sqrt{\pi}}{\mathrm{2}\left(^{\mathrm{4}} \sqrt{\mathrm{e}}\right)} \\ $$
