Question Number 106285 by bemath last updated on 04/Aug/20

$$\underset{\mathrm{0}} {\overset{\infty} {\int}}\mathrm{e}^{−\mathrm{x}^{\mathrm{2}} } \:\mathrm{dx}\:? \\ $$
Answered by bobhans last updated on 04/Aug/20
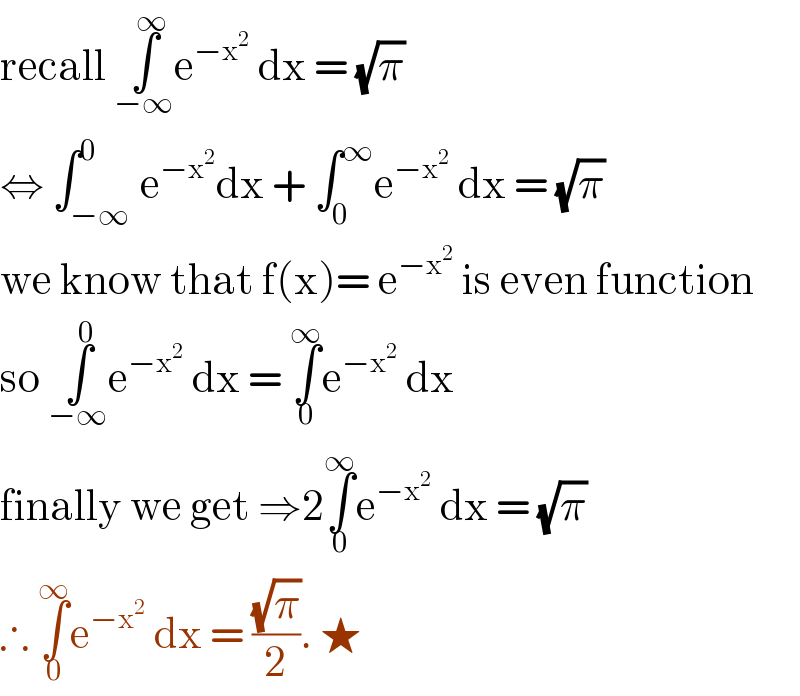
$$\mathrm{recall}\:\underset{−\infty} {\overset{\infty} {\int}}\mathrm{e}^{−\mathrm{x}^{\mathrm{2}} } \:\mathrm{dx}\:=\:\sqrt{\pi} \\ $$$$\Leftrightarrow\:\int_{−\infty} ^{\mathrm{0}} \mathrm{e}^{−\mathrm{x}^{\mathrm{2}} } \mathrm{dx}\:+\:\int_{\mathrm{0}} ^{\infty} \mathrm{e}^{−\mathrm{x}^{\mathrm{2}} } \:\mathrm{dx}\:=\:\sqrt{\pi}\: \\ $$$$\mathrm{we}\:\mathrm{know}\:\mathrm{that}\:\mathrm{f}\left(\mathrm{x}\right)=\:\mathrm{e}^{−\mathrm{x}^{\mathrm{2}} } \:\mathrm{is}\:\mathrm{even}\:\mathrm{function} \\ $$$$\mathrm{so}\:\underset{−\infty} {\overset{\mathrm{0}} {\int}}\mathrm{e}^{−\mathrm{x}^{\mathrm{2}} } \:\mathrm{dx}\:=\:\underset{\mathrm{0}} {\overset{\infty} {\int}}\mathrm{e}^{−\mathrm{x}^{\mathrm{2}} } \:\mathrm{dx} \\ $$$$\mathrm{finally}\:\mathrm{we}\:\mathrm{get}\:\Rightarrow\mathrm{2}\underset{\mathrm{0}} {\overset{\infty} {\int}}\mathrm{e}^{−\mathrm{x}^{\mathrm{2}} } \:\mathrm{dx}\:=\:\sqrt{\pi} \\ $$$$\therefore\:\underset{\mathrm{0}} {\overset{\infty} {\int}}\mathrm{e}^{−\mathrm{x}^{\mathrm{2}} } \:\mathrm{dx}\:=\:\frac{\sqrt{\pi}}{\mathrm{2}}.\:\bigstar\: \\ $$
Answered by MAB last updated on 04/Aug/20
![I=∫_0 ^∞ e^(−x^2 ) dx I^2 =(∫_0 ^∞ e^(−x^2 ) dx)(∫_0 ^∞ e^(−y^2 ) dy) I^2 =∫_0 ^∞ ∫_0 ^∞ e^(−(x^2 +y^2 )) dxdy let x=rcos(θ) and y=rsin(θ) where r≥0 and 0≤θ≤π/2 dxdy=rdrdθ I^2 =∫_0 ^(π/2) ∫_0 ^∞ re^(−r^2 ) drdθ I^2 =∫_0 ^(π/2) (1/2)[e^(−r^2 ) ]_0 ^∞ dθ I^2 =(π/4) hence I=((√π)/2)](https://www.tinkutara.com/question/Q106296.png)
$${I}=\underset{\mathrm{0}} {\overset{\infty} {\int}}\mathrm{e}^{−\mathrm{x}^{\mathrm{2}} } \:\mathrm{dx}\: \\ $$$${I}^{\mathrm{2}} =\left(\int_{\mathrm{0}} ^{\infty} {e}^{−{x}^{\mathrm{2}} } {dx}\right)\left(\int_{\mathrm{0}} ^{\infty} {e}^{−{y}^{\mathrm{2}} } {dy}\right) \\ $$$${I}^{\mathrm{2}} =\int_{\mathrm{0}} ^{\infty} \int_{\mathrm{0}} ^{\infty} {e}^{−\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} \right)} {dxdy} \\ $$$${let}\:{x}={rcos}\left(\theta\right)\:{and}\:{y}={rsin}\left(\theta\right) \\ $$$${where}\:{r}\geqslant\mathrm{0}\:{and}\:\mathrm{0}\leqslant\theta\leqslant\pi/\mathrm{2} \\ $$$${dxdy}={rdrd}\theta \\ $$$${I}^{\mathrm{2}} =\int_{\mathrm{0}} ^{\pi/\mathrm{2}} \int_{\mathrm{0}} ^{\infty} {re}^{−{r}^{\mathrm{2}} } {drd}\theta \\ $$$${I}^{\mathrm{2}} =\int_{\mathrm{0}} ^{\pi/\mathrm{2}} \frac{\mathrm{1}}{\mathrm{2}}\left[{e}^{−{r}^{\mathrm{2}} } \right]_{\mathrm{0}} ^{\infty} {d}\theta \\ $$$${I}^{\mathrm{2}} =\frac{\pi}{\mathrm{4}} \\ $$$${hence}\:{I}=\frac{\sqrt{\pi}}{\mathrm{2}} \\ $$
