Question Number 64804 by mmkkmm000m last updated on 21/Jul/19
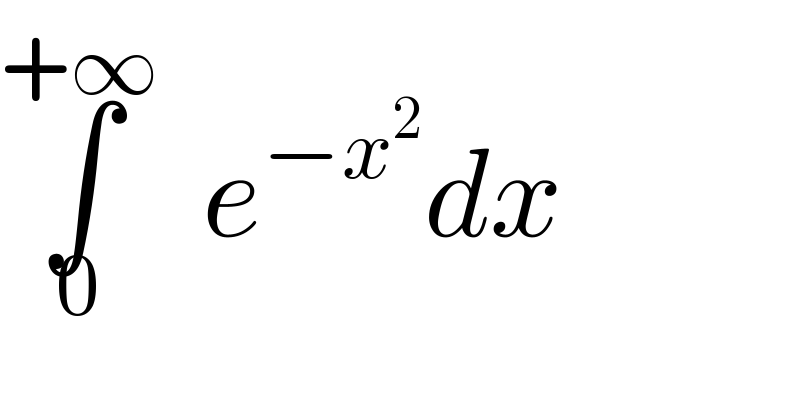
$$\overset{+\infty} {\int}_{\mathrm{0}} {e}^{−{x}^{\mathrm{2}} } {dx} \\ $$
Answered by Tanmay chaudhury last updated on 21/Jul/19
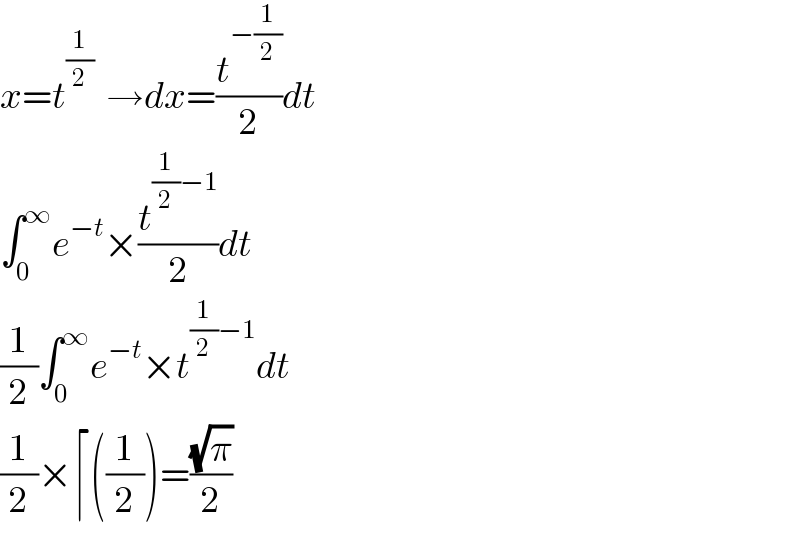
$${x}={t}^{\frac{\mathrm{1}}{\mathrm{2}}} \:\:\rightarrow{dx}=\frac{{t}^{−\frac{\mathrm{1}}{\mathrm{2}}} }{\mathrm{2}}{dt} \\ $$$$\int_{\mathrm{0}} ^{\infty} {e}^{−{t}} ×\frac{{t}^{\frac{\mathrm{1}}{\mathrm{2}}−\mathrm{1}} }{\mathrm{2}}{dt} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\infty} {e}^{−{t}} ×{t}^{\frac{\mathrm{1}}{\mathrm{2}}−\mathrm{1}} {dt} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}×\lceil\left(\frac{\mathrm{1}}{\mathrm{2}}\right)=\frac{\sqrt{\pi}}{\mathrm{2}} \\ $$
