Menu Close

0-e-x-2-ln-x-x-dx-1-4-

Tinku Tara 0 Comments
Pin




Question Number 162924 by mnjuly1970 last updated on 02/Jan/22
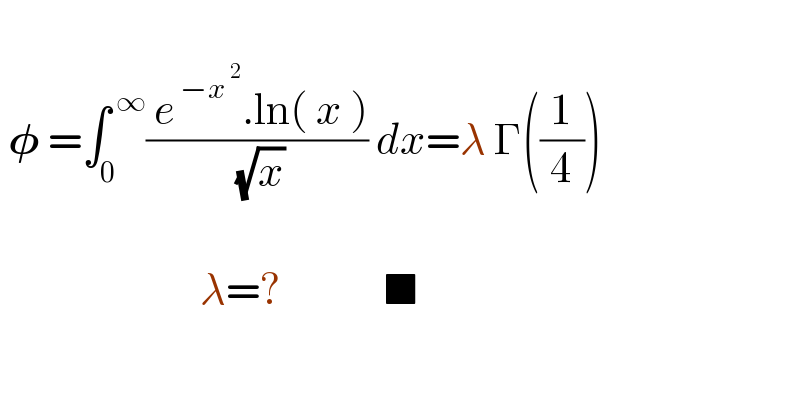
𝛗 =∫_0 ^( ∞) (( e^( −x^( 2) ) .ln( x ))/( (√x))) dx=λ Γ((1/4)) λ=? ■
$$\: \\ $$$$\:\boldsymbol{\phi}\:=\int_{\mathrm{0}} ^{\:\infty} \frac{\:{e}^{\:−{x}^{\:\mathrm{2}} } .\mathrm{ln}\left(\:{x}\:\right)}{\:\sqrt{{x}}}\:{dx}=\lambda\:\Gamma\left(\frac{\mathrm{1}}{\mathrm{4}}\right) \\ $$$$ \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\lambda=?\:\:\:\:\:\:\:\:\:\:\:\:\:\blacksquare \\ $$$$ \\ $$
Answered by Lordose last updated on 02/Jan/22
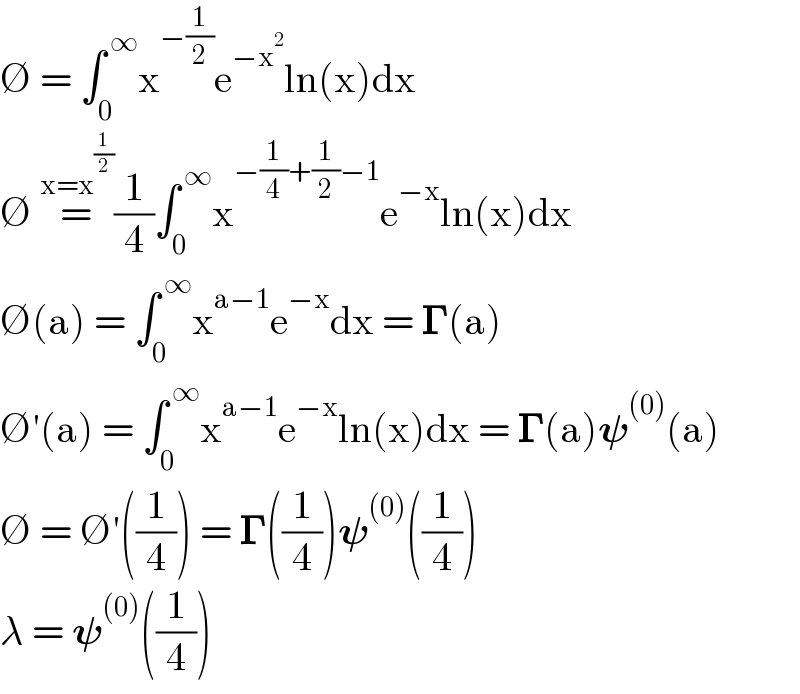
∅ = ∫_0 ^( ∞) x^(−(1/2)) e^(−x^2 ) ln(x)dx ∅ =^(x=x^(1/2) ) (1/4)∫_0 ^( ∞) x^(−(1/4)+(1/2)−1) e^(−x) ln(x)dx ∅(a) = ∫_0 ^( ∞) x^(a−1) e^(−x) dx = 𝚪(a) ∅′(a) = ∫_0 ^( ∞) x^(a−1) e^(−x) ln(x)dx = 𝚪(a)𝛙^((0)) (a) ∅ = ∅′((1/4)) = 𝚪((1/4))𝛙^((0)) ((1/4)) λ = 𝛙^((0)) ((1/4))
$$\varnothing\:=\:\int_{\mathrm{0}} ^{\:\infty} \mathrm{x}^{−\frac{\mathrm{1}}{\mathrm{2}}} \mathrm{e}^{−\mathrm{x}^{\mathrm{2}} } \mathrm{ln}\left(\mathrm{x}\right)\mathrm{dx} \\ $$$$\varnothing\:\overset{\mathrm{x}=\mathrm{x}^{\frac{\mathrm{1}}{\mathrm{2}}} } {=}\frac{\mathrm{1}}{\mathrm{4}}\int_{\mathrm{0}} ^{\:\infty} \mathrm{x}^{−\frac{\mathrm{1}}{\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{2}}−\mathrm{1}} \mathrm{e}^{−\mathrm{x}} \mathrm{ln}\left(\mathrm{x}\right)\mathrm{dx} \\ $$$$\varnothing\left(\mathrm{a}\right)\:=\:\int_{\mathrm{0}} ^{\:\infty} \mathrm{x}^{\mathrm{a}−\mathrm{1}} \mathrm{e}^{−\mathrm{x}} \mathrm{dx}\:=\:\boldsymbol{\Gamma}\left(\mathrm{a}\right) \\ $$$$\varnothing'\left(\mathrm{a}\right)\:=\:\int_{\mathrm{0}} ^{\:\infty} \mathrm{x}^{\mathrm{a}−\mathrm{1}} \mathrm{e}^{−\mathrm{x}} \mathrm{ln}\left(\mathrm{x}\right)\mathrm{dx}\:=\:\boldsymbol{\Gamma}\left(\mathrm{a}\right)\boldsymbol{\psi}^{\left(\mathrm{0}\right)} \left(\mathrm{a}\right) \\ $$$$\varnothing\:=\:\varnothing'\left(\frac{\mathrm{1}}{\mathrm{4}}\right)\:=\:\boldsymbol{\Gamma}\left(\frac{\mathrm{1}}{\mathrm{4}}\right)\boldsymbol{\psi}^{\left(\mathrm{0}\right)} \left(\frac{\mathrm{1}}{\mathrm{4}}\right) \\ $$$$\lambda\:=\:\boldsymbol{\psi}^{\left(\mathrm{0}\right)} \left(\frac{\mathrm{1}}{\mathrm{4}}\right) \\ $$
Commented by mnjuly1970 last updated on 02/Jan/22
thanks alot sir lordose
$${thanks}\:{alot}\:{sir}\:{lordose} \\ $$
Answered by mathmax by abdo last updated on 02/Jan/22
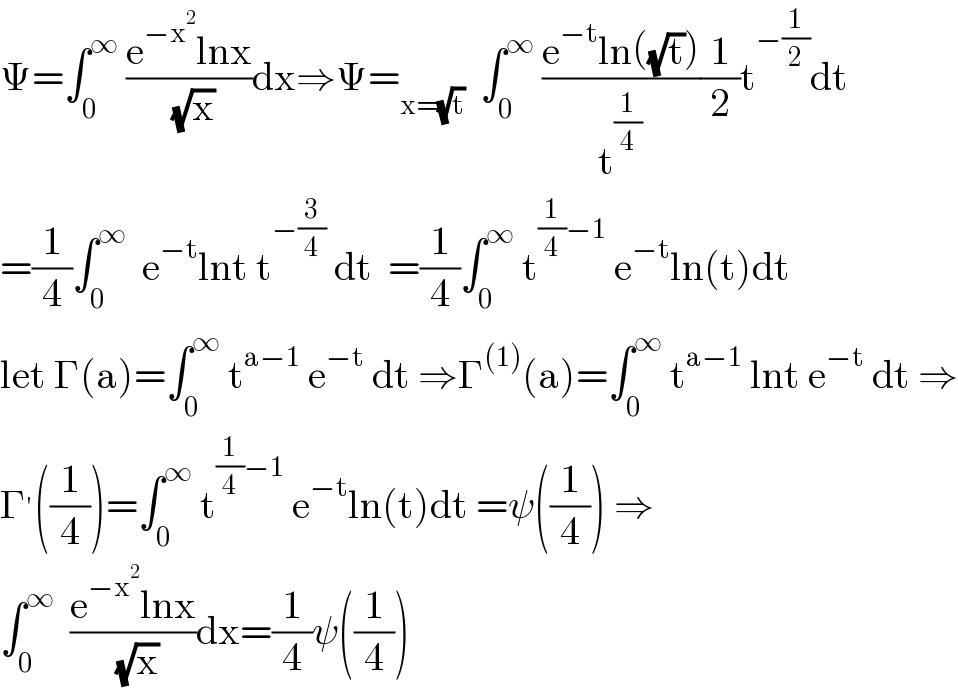
Ψ=∫_0 ^∞ ((e^(−x^2 ) lnx)/( (√x)))dx⇒Ψ=_(x=(√t)) ∫_0 ^∞ ((e^(−t) ln((√t)))/t^(1/4) )(1/2)t^(−(1/2)) dt =(1/4)∫_0 ^∞ e^(−t) lnt t^(−(3/4)) dt =(1/4)∫_0 ^∞ t^((1/4)−1) e^(−t) ln(t)dt let Γ(a)=∫_0 ^∞ t^(a−1) e^(−t) dt ⇒Γ^((1)) (a)=∫_0 ^∞ t^(a−1) lnt e^(−t) dt ⇒ Γ^′ ((1/4))=∫_0 ^∞ t^((1/4)−1) e^(−t) ln(t)dt =ψ((1/4)) ⇒ ∫_0 ^∞ ((e^(−x^2 ) lnx)/( (√x)))dx=(1/4)ψ((1/4))
$$\Psi=\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{e}^{−\mathrm{x}^{\mathrm{2}} } \mathrm{lnx}}{\:\sqrt{\mathrm{x}}}\mathrm{dx}\Rightarrow\Psi=_{\mathrm{x}=\sqrt{\mathrm{t}}} \:\:\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{e}^{−\mathrm{t}} \mathrm{ln}\left(\sqrt{\mathrm{t}}\right)}{\mathrm{t}^{\frac{\mathrm{1}}{\mathrm{4}}} }\frac{\mathrm{1}}{\mathrm{2}}\mathrm{t}^{−\frac{\mathrm{1}}{\mathrm{2}}} \mathrm{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\int_{\mathrm{0}} ^{\infty} \:\:\mathrm{e}^{−\mathrm{t}} \mathrm{lnt}\:\mathrm{t}^{−\frac{\mathrm{3}}{\mathrm{4}}} \:\mathrm{dt}\:\:=\frac{\mathrm{1}}{\mathrm{4}}\int_{\mathrm{0}} ^{\infty} \:\mathrm{t}^{\frac{\mathrm{1}}{\mathrm{4}}−\mathrm{1}} \:\mathrm{e}^{−\mathrm{t}} \mathrm{ln}\left(\mathrm{t}\right)\mathrm{dt} \\ $$$$\mathrm{let}\:\Gamma\left(\mathrm{a}\right)=\int_{\mathrm{0}} ^{\infty} \:\mathrm{t}^{\mathrm{a}−\mathrm{1}} \:\mathrm{e}^{−\mathrm{t}} \:\mathrm{dt}\:\Rightarrow\Gamma^{\left(\mathrm{1}\right)} \left(\mathrm{a}\right)=\int_{\mathrm{0}} ^{\infty} \:\mathrm{t}^{\mathrm{a}−\mathrm{1}} \:\mathrm{lnt}\:\mathrm{e}^{−\mathrm{t}} \:\mathrm{dt}\:\Rightarrow \\ $$$$\Gamma^{'} \left(\frac{\mathrm{1}}{\mathrm{4}}\right)=\int_{\mathrm{0}} ^{\infty} \:\mathrm{t}^{\frac{\mathrm{1}}{\mathrm{4}}−\mathrm{1}} \:\mathrm{e}^{−\mathrm{t}} \mathrm{ln}\left(\mathrm{t}\right)\mathrm{dt}\:=\psi\left(\frac{\mathrm{1}}{\mathrm{4}}\right)\:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{e}^{−\mathrm{x}^{\mathrm{2}} } \mathrm{lnx}}{\:\sqrt{\mathrm{x}}}\mathrm{dx}=\frac{\mathrm{1}}{\mathrm{4}}\psi\left(\frac{\mathrm{1}}{\mathrm{4}}\right) \\ $$
Commented by mathmax by abdo last updated on 03/Jan/22
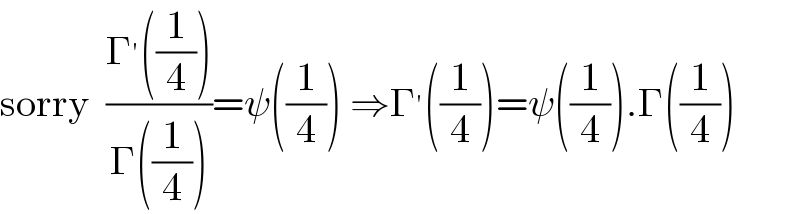
sorry ((Γ^′ ((1/4)))/(Γ((1/4))))=ψ((1/4)) ⇒Γ^′ ((1/4))=ψ((1/4)).Γ((1/4))
$$\mathrm{sorry}\:\:\frac{\Gamma^{'} \left(\frac{\mathrm{1}}{\mathrm{4}}\right)}{\Gamma\left(\frac{\mathrm{1}}{\mathrm{4}}\right)}=\psi\left(\frac{\mathrm{1}}{\mathrm{4}}\right)\:\Rightarrow\Gamma^{'} \left(\frac{\mathrm{1}}{\mathrm{4}}\right)=\psi\left(\frac{\mathrm{1}}{\mathrm{4}}\right).\Gamma\left(\frac{\mathrm{1}}{\mathrm{4}}\right) \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *