Menu Close

0-e-x-2-x-2-1-dx-

Tinku Tara 0 Comments
Pin




Question Number 33531 by Yozzzzy last updated on 18/Apr/18
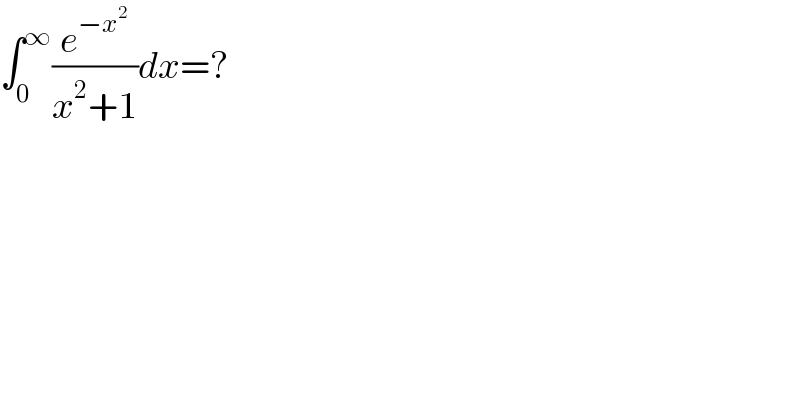
∫_0 ^∞ (e^(−x^2 ) /(x^2 +1))dx=?
$$\int_{\mathrm{0}} ^{\infty} \frac{{e}^{−{x}^{\mathrm{2}} } }{{x}^{\mathrm{2}} +\mathrm{1}}{dx}=? \\ $$
Commented by Rasheed.Sindhi last updated on 18/Apr/18
Ve....ry happy to see you back again, if you are old Yozzi!
$$\mathrm{Ve}….\mathrm{ry}\:\mathrm{happy}\:\mathrm{to}\:\mathrm{see}\:\mathrm{you}\:\mathrm{back}\:\mathrm{again},\: \\ $$$$\mathrm{if}\:\mathrm{you}\:\mathrm{are}\:\:\mathrm{old}\:\mathrm{Yozzi}! \\ $$
Commented by NECx last updated on 18/Apr/18
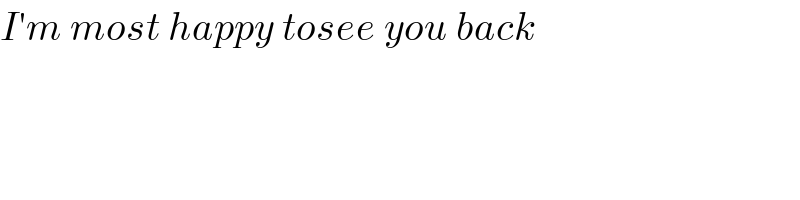
I′m most happy tosee you back
$${I}'{m}\:{most}\:{happy}\:{tosee}\:{you}\:{back} \\ $$
Commented by math khazana by abdo last updated on 18/Apr/18
let put I = ∫_0 ^∞ (e^(−x^2 ) /(x^2 +1)) dx we have 2I = ∫_(−∞) ^(+∞) (e^(−x^2 ) /(x^2 +1))dx .let consider the complex function ϕ(z) = (e^(−z^2 ) /(1+z^2 )) .the poles of ϕ are i and −i (simples) Residus theorem give ∫_(−∞) ^(+∞) ϕ(z)dz =2i π Res(ϕ,i) Res(ϕ,i) =lim_(z→i) (z−i)ϕ(z)=lim_(z→i) (z−i) (e^(−z^2 ) /((z−i)(z+i))) = (e^(−i^2 ) /(2i)) = (e/(2i)) ⇒ 2I = 2iπ.(e/(2i)) = πe ⇒ ★ I = ((π e)/2) ★
$${let}\:{put}\:{I}\:\:=\:\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{{e}^{−{x}^{\mathrm{2}} } }{{x}^{\mathrm{2}} \:+\mathrm{1}}\:{dx}\:\:{we}\:{have}\: \\ $$$$\mathrm{2}{I}\:\:=\:\int_{−\infty} ^{+\infty} \:\:\:\frac{{e}^{−{x}^{\mathrm{2}} } }{{x}^{\mathrm{2}} \:+\mathrm{1}}{dx}\:.{let}\:{consider}\:{the}\:{complex}\:{function} \\ $$$$\varphi\left({z}\right)\:=\:\frac{{e}^{−{z}^{\mathrm{2}} } }{\mathrm{1}+{z}^{\mathrm{2}} }\:\:.{the}\:{poles}\:{of}\:\varphi\:{are}\:{i}\:{and}\:−{i}\:\left({simples}\right) \\ $$$${Residus}\:{theorem}\:{give}\: \\ $$$$\int_{−\infty} ^{+\infty} \:\varphi\left({z}\right){dz}\:=\mathrm{2}{i}\:\pi\:{Res}\left(\varphi,{i}\right)\: \\ $$$${Res}\left(\varphi,{i}\right)\:={lim}_{{z}\rightarrow{i}} \:\left({z}−{i}\right)\varphi\left({z}\right)={lim}_{{z}\rightarrow{i}} \left({z}−{i}\right)\:\frac{{e}^{−{z}^{\mathrm{2}} } }{\left({z}−{i}\right)\left({z}+{i}\right)} \\ $$$$=\:\frac{{e}^{−{i}^{\mathrm{2}} } }{\mathrm{2}{i}}\:\:=\:\frac{{e}}{\mathrm{2}{i}}\:\Rightarrow\:\mathrm{2}{I}\:\:=\:\mathrm{2}{i}\pi.\frac{{e}}{\mathrm{2}{i}}\:=\:\pi{e}\:\Rightarrow \\ $$$$\bigstar\:\:{I}\:=\:\frac{\pi\:{e}}{\mathrm{2}}\:\bigstar \\ $$
Commented by MJS last updated on 18/Apr/18
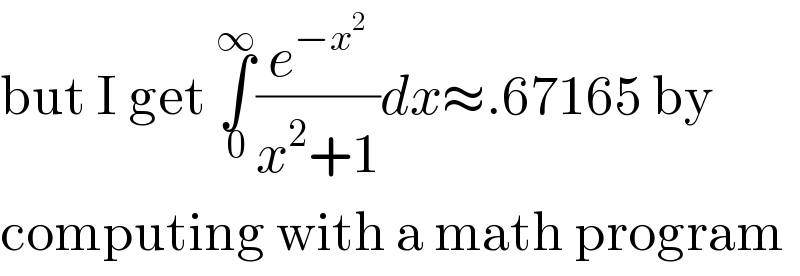
but I get ∫_0 ^∞ (e^(−x^2 ) /(x^2 +1))dx≈.67165 by computing with a math program
$$\mathrm{but}\:\mathrm{I}\:\mathrm{get}\:\underset{\mathrm{0}} {\overset{\infty} {\int}}\frac{{e}^{−{x}^{\mathrm{2}} } }{{x}^{\mathrm{2}} +\mathrm{1}}{dx}\approx.\mathrm{67165}\:\mathrm{by} \\ $$$$\mathrm{computing}\:\mathrm{with}\:\mathrm{a}\:\mathrm{math}\:\mathrm{program} \\ $$
Commented by math khazana by abdo last updated on 19/Apr/18
your math programe is not correct sir the residus theorem have fixed the result ...
$${your}\:{math}\:{programe}\:{is}\:{not}\:{correct}\:{sir}\:\:{the}\:{residus} \\ $$$${theorem}\:{have}\:{fixed}\:\:{the}\:{result}\:… \\ $$
Commented by MJS last updated on 19/Apr/18
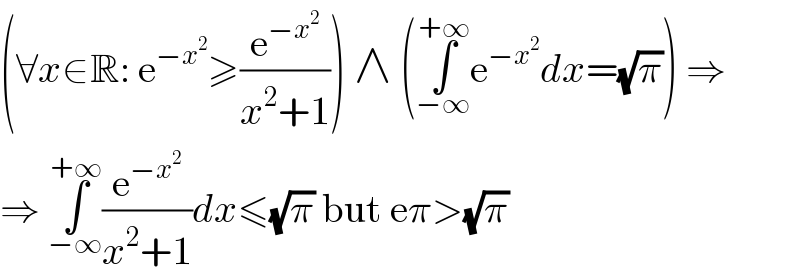
(∀x∈R: e^(−x^2 ) ≥(e^(−x^2 ) /(x^2 +1))) ∧ (∫_(−∞) ^(+∞) e^(−x^2 ) dx=(√π)) ⇒ ⇒ ∫_(−∞) ^(+∞) (e^(−x^2 ) /(x^2 +1))dx≤(√π) but eπ>(√π)
$$\left(\forall{x}\in\mathbb{R}:\:\mathrm{e}^{−{x}^{\mathrm{2}} } \geqslant\frac{\mathrm{e}^{−{x}^{\mathrm{2}} } }{{x}^{\mathrm{2}} +\mathrm{1}}\right)\:\wedge\:\left(\underset{−\infty} {\overset{+\infty} {\int}}\mathrm{e}^{−{x}^{\mathrm{2}} } {dx}=\sqrt{\pi}\right)\:\Rightarrow \\ $$$$\Rightarrow\:\underset{−\infty} {\overset{+\infty} {\int}}\frac{\mathrm{e}^{−{x}^{\mathrm{2}} } }{{x}^{\mathrm{2}} +\mathrm{1}}{dx}\leqslant\sqrt{\pi}\:\mathrm{but}\:\mathrm{e}\pi>\sqrt{\pi} \\ $$
Commented by math khazana by abdo last updated on 19/Apr/18
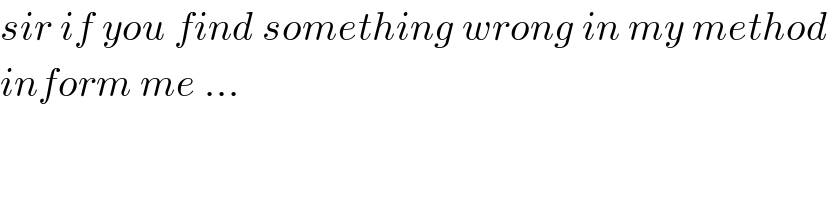
sir if you find something wrong in my method inform me ...
$${sir}\:{if}\:{you}\:{find}\:{something}\:{wrong}\:{in}\:{my}\:{method} \\ $$$${inform}\:{me}\:… \\ $$
Commented by MJS last updated on 19/Apr/18
the method seems ok, I′m not sure what′s going on here... I will keep on studying this problem and post the answer if I can find it
$$\mathrm{the}\:\mathrm{method}\:\mathrm{seems}\:\mathrm{ok},\:\mathrm{I}'\mathrm{m}\:\mathrm{not}\:\mathrm{sure}\:\mathrm{what}'\mathrm{s} \\ $$$$\mathrm{going}\:\mathrm{on}\:\mathrm{here}…\:\mathrm{I}\:\mathrm{will}\:\mathrm{keep}\:\mathrm{on}\:\mathrm{studying}\:\mathrm{this} \\ $$$$\mathrm{problem}\:\mathrm{and}\:\mathrm{post}\:\mathrm{the}\:\mathrm{answer}\:\mathrm{if}\:\mathrm{I}\:\mathrm{can}\:\mathrm{find}\:\mathrm{it} \\ $$
Commented by math khazana by abdo last updated on 19/Apr/18
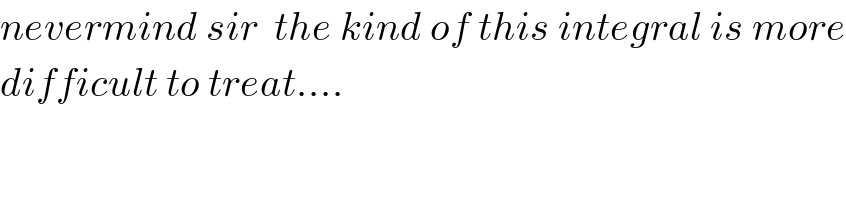
nevermind sir the kind of this integral is more difficult to treat....
$${nevermind}\:{sir}\:\:{the}\:{kind}\:{of}\:{this}\:{integral}\:{is}\:{more} \\ $$$${difficult}\:{to}\:{treat}…. \\ $$
Commented by MJS last updated on 20/Apr/18
I found this on the internet: ∫_0 ^∞ (e^(−x^2 ) /(x^2 +1))dx=((eπ)/2)×erfc(1)=((eπ)/2)×(2/( (√π)))∫_1 ^∞ e^(−t^2 ) dt= =e(√π)×0.139402792...=0.671646710... erfc(x)=(2/( (√π)))∫_x ^∞ e^(−t^2 ) dt so we would need to find r=∫_1 ^∞ e^(−t^2 ) dt=∫_0 ^∞ e^(−(t+1)^2 ) dt but there′s no exact solution for r
$$\mathrm{I}\:\mathrm{found}\:\mathrm{this}\:\mathrm{on}\:\mathrm{the}\:\mathrm{internet}: \\ $$$$\underset{\mathrm{0}} {\overset{\infty} {\int}}\frac{\mathrm{e}^{−{x}^{\mathrm{2}} } }{{x}^{\mathrm{2}} +\mathrm{1}}{dx}=\frac{\mathrm{e}\pi}{\mathrm{2}}×{erfc}\left(\mathrm{1}\right)=\frac{\mathrm{e}\pi}{\mathrm{2}}×\frac{\mathrm{2}}{\:\sqrt{\pi}}\underset{\mathrm{1}} {\overset{\infty} {\int}}\mathrm{e}^{−{t}^{\mathrm{2}} } {dt}= \\ $$$$=\mathrm{e}\sqrt{\pi}×\mathrm{0}.\mathrm{139402792}…=\mathrm{0}.\mathrm{671646710}… \\ $$$${erfc}\left({x}\right)=\frac{\mathrm{2}}{\:\sqrt{\pi}}\underset{{x}} {\overset{\infty} {\int}}\mathrm{e}^{−{t}^{\mathrm{2}} } {dt} \\ $$$$\mathrm{so}\:\mathrm{we}\:\mathrm{would}\:\mathrm{need}\:\mathrm{to}\:\mathrm{find} \\ $$$${r}=\underset{\mathrm{1}} {\overset{\infty} {\int}}\mathrm{e}^{−{t}^{\mathrm{2}} } {dt}=\underset{\mathrm{0}} {\overset{\infty} {\int}}\mathrm{e}^{−\left({t}+\mathrm{1}\right)^{\mathrm{2}} } {dt} \\ $$$$\mathrm{but}\:\mathrm{there}'\mathrm{s}\:\mathrm{no}\:\mathrm{exact}\:\mathrm{solution}\:\mathrm{for}\:{r} \\ $$
Commented by abdo imad last updated on 20/Apr/18
thank you sir for this clarification for ∫_1 ^(+∞) e^(−t^2 ) dx we can give a approximat value...
$${thank}\:{you}\:{sir}\:{for}\:{this}\:{clarification}\:{for}\:\int_{\mathrm{1}} ^{+\infty} \:{e}^{−{t}^{\mathrm{2}} } {dx}\:{we}\:{can} \\ $$$${give}\:{a}\:{approximat}\:{value}… \\ $$
Commented by abdo imad last updated on 20/Apr/18
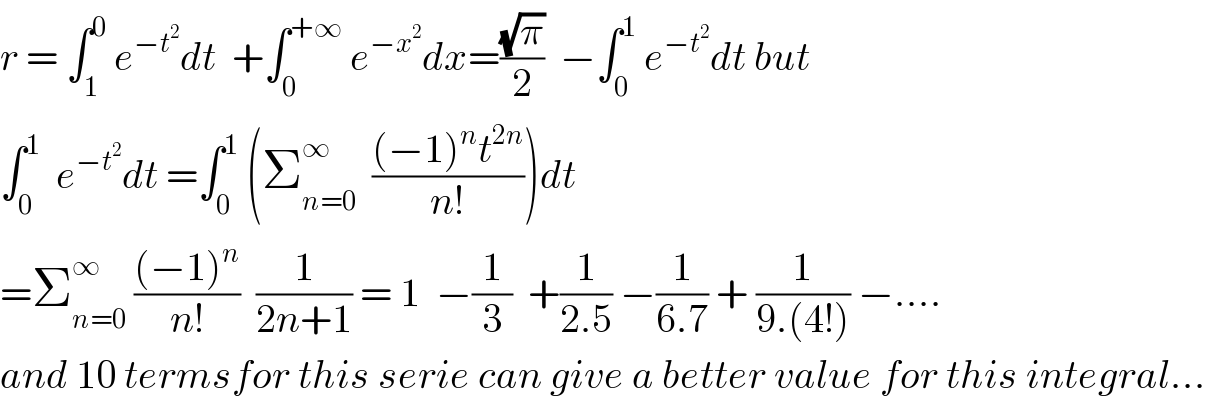
r = ∫_1 ^0 e^(−t^2 ) dt +∫_0 ^(+∞) e^(−x^2 ) dx=((√π)/2) −∫_0 ^1 e^(−t^2 ) dt but ∫_0 ^1 e^(−t^2 ) dt =∫_0 ^1 (Σ_(n=0) ^∞ (((−1)^n t^(2n) )/(n!)))dt =Σ_(n=0) ^∞ (((−1)^n )/(n!)) (1/(2n+1)) = 1 −(1/3) +(1/(2.5)) −(1/(6.7)) + (1/(9.(4!))) −.... and 10 termsfor this serie can give a better value for this integral...
$${r}\:=\:\int_{\mathrm{1}} ^{\mathrm{0}} \:{e}^{−{t}^{\mathrm{2}} } {dt}\:\:+\int_{\mathrm{0}} ^{+\infty} \:{e}^{−{x}^{\mathrm{2}} } {dx}=\frac{\sqrt{\pi}}{\mathrm{2}}\:\:−\int_{\mathrm{0}} ^{\mathrm{1}} \:{e}^{−{t}^{\mathrm{2}} } {dt}\:{but} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \:\:{e}^{−{t}^{\mathrm{2}} } {dt}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\left(\sum_{{n}=\mathrm{0}} ^{\infty} \:\:\frac{\left(−\mathrm{1}\right)^{{n}} {t}^{\mathrm{2}{n}} }{{n}!}\right){dt} \\ $$$$=\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}} }{{n}!}\:\:\frac{\mathrm{1}}{\mathrm{2}{n}+\mathrm{1}}\:=\:\mathrm{1}\:\:−\frac{\mathrm{1}}{\mathrm{3}}\:\:+\frac{\mathrm{1}}{\mathrm{2}.\mathrm{5}}\:−\frac{\mathrm{1}}{\mathrm{6}.\mathrm{7}}\:+\:\frac{\mathrm{1}}{\mathrm{9}.\left(\mathrm{4}!\right)}\:−…. \\ $$$${and}\:\mathrm{10}\:{termsfor}\:{this}\:{serie}\:{can}\:{give}\:{a}\:{better}\:{value}\:{for}\:{this}\:{integral}… \\ $$
Commented by MJS last updated on 20/Apr/18
thank you
$$\mathrm{thank}\:\mathrm{you} \\ $$
Commented by Yozzzzy last updated on 21/Apr/18
Yes it′s me. I′ve just been so busy with university that I have little time during the academic year to contribute to this forum. I′m glad it has stayed active since I started uni. I′ve got an answer for the integral which involves integrating under the integral sign. One may consider the integral ∫_(−∞) ^∞ (e^(−b(x^2 +1)) /(x^2 +1))dx where b≥0 and create differential equation with b as the indepedent variable. Initially I tried using complex analysis but found much difficulty in obtaining a suitable contour. Nonetheless, I was able to get something out of the attempts, these integrals: 1)∫_0 ^∞ ((cos(x^2 )−sin(x^2 ))/(1+x^4 ))dx=(π/4)e^(−1) (√2) 2)∫_0 ^∞ ((x^2 (cos(x^2 )+sin(x^2 )))/(1+x^4 ))dx=(π/4)e^(−1) (√2) Hence ∫_0 ^∞ (((x^2 +1)sin(x^2 )+(x^2 −1)cos(x^2 ))/(1+x^4 ))dx=0.
$${Yes}\:{it}'{s}\:{me}.\:{I}'{ve}\:{just}\:{been}\:{so}\:{busy}\:{with}\: \\ $$$${university}\:{that}\:{I}\:{have}\:{little}\:{time}\:{during}\: \\ $$$${the}\:{academic}\:{year}\:{to}\:{contribute}\:{to}\:{this}\: \\ $$$${forum}.\:{I}'{m}\:{glad}\:{it}\:{has}\:{stayed}\:{active}\:{since} \\ $$$${I}\:{started}\:{uni}.\:{I}'{ve}\:{got}\:{an}\:{answer}\:{for}\:{the}\: \\ $$$${integral}\:{which}\:{involves}\:{integrating}\:{under} \\ $$$${the}\:{integral}\:{sign}.\:{One}\:{may}\:{consider}\:{the}\: \\ $$$${integral}\:\int_{−\infty} ^{\infty} \frac{{e}^{−{b}\left({x}^{\mathrm{2}} +\mathrm{1}\right)} }{{x}^{\mathrm{2}} +\mathrm{1}}{dx}\:{where}\:{b}\geqslant\mathrm{0} \\ $$$${and}\:{create}\:{differential}\:{equation}\:{with}\:{b}\:{as} \\ $$$${the}\:{indepedent}\:{variable}. \\ $$$${Initially}\:{I}\:{tried}\:{using}\:{complex}\:{analysis} \\ $$$${but}\:{found}\:{much}\:{difficulty}\:{in}\:{obtaining}\:{a}\: \\ $$$${suitable}\:{contour}.\:{Nonetheless},\:{I}\:{was}\:{able}\:{to}\: \\ $$$${get}\:{something}\:{out}\:{of}\:{the}\:{attempts},\:{these}\:{integrals}: \\ $$$$\left.\mathrm{1}\right)\int_{\mathrm{0}} ^{\infty} \frac{{cos}\left({x}^{\mathrm{2}} \right)−{sin}\left({x}^{\mathrm{2}} \right)}{\mathrm{1}+{x}^{\mathrm{4}} }{dx}=\frac{\pi}{\mathrm{4}}{e}^{−\mathrm{1}} \sqrt{\mathrm{2}} \\ $$$$\left.\mathrm{2}\right)\int_{\mathrm{0}} ^{\infty} \frac{{x}^{\mathrm{2}} \left({cos}\left({x}^{\mathrm{2}} \right)+{sin}\left({x}^{\mathrm{2}} \right)\right)}{\mathrm{1}+{x}^{\mathrm{4}} }{dx}=\frac{\pi}{\mathrm{4}}{e}^{−\mathrm{1}} \sqrt{\mathrm{2}} \\ $$$${Hence}\:\int_{\mathrm{0}} ^{\infty} \frac{\left({x}^{\mathrm{2}} +\mathrm{1}\right){sin}\left({x}^{\mathrm{2}} \right)+\left({x}^{\mathrm{2}} −\mathrm{1}\right){cos}\left({x}^{\mathrm{2}} \right)}{\mathrm{1}+{x}^{\mathrm{4}} }{dx}=\mathrm{0}. \\ $$$$ \\ $$
Commented by Rasheed.Sindhi last updated on 23/Apr/18
Did you complete your graduation?
$$\mathrm{Did}\:\mathrm{you}\:\mathrm{complete}\:\mathrm{your}\:\mathrm{graduation}? \\ $$
Commented by Yozzzzy last updated on 24/Apr/18
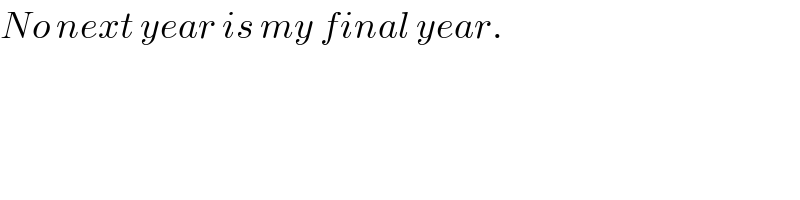
No next year is my final year.
$${No}\:{next}\:{year}\:{is}\:{my}\:{final}\:{year}.\: \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *