0-e-x-2-x-2-a-2-2-dx-

Question Number 174727 by princeDera last updated on 09/Aug/22

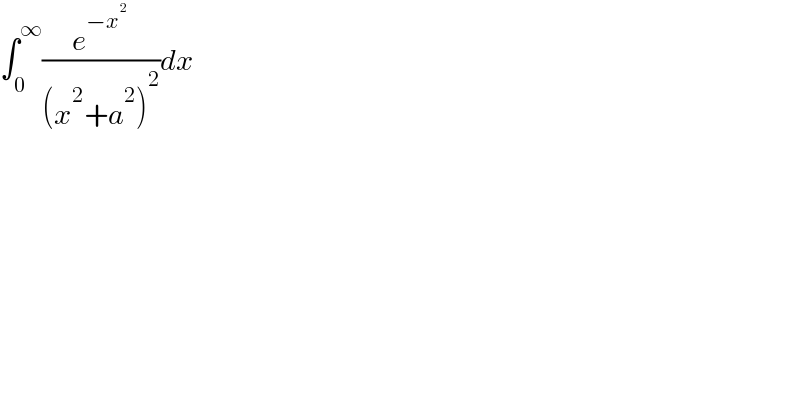
$$\int_{\mathrm{0}} ^{\infty} \frac{{e}^{−{x}^{\mathrm{2}} } }{\left({x}^{\mathrm{2}} +{a}^{\mathrm{2}} \right)^{\mathrm{2}} }{dx} \\ $$

Answered by aleks041103 last updated on 10/Aug/22

∫_0 ^∞ (1/(x^2 +a^2 )) (e^(−x^2 ) /(x^2 +a^2 ))dx= =(1/a^2 )∫(((x^2 +a^2 −x^2 ))/(x^2 +a^2 )) (e^(−x^2 ) /(x^2 +a^2 ))dx= =(1/a^2 )∫_0 ^∞ (e^(−x^2 ) /(a^2 +x^2 ))dx+(1/a^2 )∫_0 ^∞ ((−x^2 e^(−x^2 ) )/((x^2 +a^2 )^2 ))dx ∫_0 ^∞ ((−x^2 e^(−x^2 ) )/((x^2 +a^2 )^2 ))dx=(1/2)∫_0 ^∞ xe^(−x^2 ) (−((2xdx)/((x^2 +a^2 )^2 )))= =(1/2)∫_0 ^∞ xe^(−x^2 ) d((1/(x^2 +a^2 )))= =[((xe^(−x^2 ) )/(2(x^2 +a^2 )))]_0 ^∞ −(1/2)∫_0 ^∞ (1/(x^2 +a^2 ))(e^(−x^2 ) −2x^2 e^(−x^2 ) )dx= =∫_0 ^∞ ((x^2 e^(−x^2 ) )/(x^2 +a^2 ))dx−(1/2)∫_0 ^∞ (e^(−x^2 ) /(x^2 +a^2 ))dx= =∫_0 ^∞ (1−(a^2 /(x^2 +a^2 )))e^(−x^2 ) dx−(1/2)∫_0 ^∞ (e^(−x^2 ) /(x^2 +a^2 ))dx= =∫_0 ^∞ e^(−x^2 ) dx−((1/2)+a^2 )∫_0 ^∞ ((e^(−x^2 ) dx)/(x^2 +a^2 ))= =((√π)/2)−((1/2)+a^2 )∫_0 ^∞ ((e^(−x^2 ) dx)/(x^2 +a^2 )) ⇒∫_0 ^∞ (e^(−x^2 ) /((x^2 +a^2 )^2 ))dx=((√π)/(2a^2 ))+((1/(2a^2 ))−1)∫_0 ^∞ ((e^(−x^2 ) dx)/(x^2 +a^2 ))

$$\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{1}}{{x}^{\mathrm{2}} +{a}^{\mathrm{2}} }\:\frac{{e}^{−{x}^{\mathrm{2}} } }{{x}^{\mathrm{2}} +{a}^{\mathrm{2}} }{dx}= \\ $$$$=\frac{\mathrm{1}}{{a}^{\mathrm{2}} }\int\frac{\left({x}^{\mathrm{2}} +{a}^{\mathrm{2}} −{x}^{\mathrm{2}} \right)}{{x}^{\mathrm{2}} +{a}^{\mathrm{2}} }\:\frac{{e}^{−{x}^{\mathrm{2}} } }{{x}^{\mathrm{2}} +{a}^{\mathrm{2}} }{dx}= \\ $$$$=\frac{\mathrm{1}}{{a}^{\mathrm{2}} }\int_{\mathrm{0}} ^{\infty} \frac{{e}^{−{x}^{\mathrm{2}} } }{{a}^{\mathrm{2}} +{x}^{\mathrm{2}} }{dx}+\frac{\mathrm{1}}{{a}^{\mathrm{2}} }\int_{\mathrm{0}} ^{\infty} \frac{−{x}^{\mathrm{2}} {e}^{−{x}^{\mathrm{2}} } }{\left({x}^{\mathrm{2}} +{a}^{\mathrm{2}} \right)^{\mathrm{2}} }{dx} \\ $$$$\int_{\mathrm{0}} ^{\infty} \frac{−{x}^{\mathrm{2}} {e}^{−{x}^{\mathrm{2}} } }{\left({x}^{\mathrm{2}} +{a}^{\mathrm{2}} \right)^{\mathrm{2}} }{dx}=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\infty} {xe}^{−{x}^{\mathrm{2}} } \left(−\frac{\mathrm{2}{xdx}}{\left({x}^{\mathrm{2}} +{a}^{\mathrm{2}} \right)^{\mathrm{2}} }\right)= \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\infty} {xe}^{−{x}^{\mathrm{2}} } {d}\left(\frac{\mathrm{1}}{{x}^{\mathrm{2}} +{a}^{\mathrm{2}} }\right)= \\ $$$$=\left[\frac{{xe}^{−{x}^{\mathrm{2}} } }{\mathrm{2}\left({x}^{\mathrm{2}} +{a}^{\mathrm{2}} \right)}\right]_{\mathrm{0}} ^{\infty} −\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{1}}{{x}^{\mathrm{2}} +{a}^{\mathrm{2}} }\left({e}^{−{x}^{\mathrm{2}} } −\mathrm{2}{x}^{\mathrm{2}} {e}^{−{x}^{\mathrm{2}} } \right){dx}= \\ $$$$=\int_{\mathrm{0}} ^{\infty} \frac{{x}^{\mathrm{2}} {e}^{−{x}^{\mathrm{2}} } }{{x}^{\mathrm{2}} +{a}^{\mathrm{2}} }{dx}−\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\infty} \frac{{e}^{−{x}^{\mathrm{2}} } }{{x}^{\mathrm{2}} +{a}^{\mathrm{2}} }{dx}= \\ $$$$=\int_{\mathrm{0}} ^{\infty} \left(\mathrm{1}−\frac{{a}^{\mathrm{2}} }{{x}^{\mathrm{2}} +{a}^{\mathrm{2}} }\right){e}^{−{x}^{\mathrm{2}} } {dx}−\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\infty} \frac{{e}^{−{x}^{\mathrm{2}} } }{{x}^{\mathrm{2}} +{a}^{\mathrm{2}} }{dx}= \\ $$$$=\int_{\mathrm{0}} ^{\infty} {e}^{−{x}^{\mathrm{2}} } {dx}−\left(\frac{\mathrm{1}}{\mathrm{2}}+{a}^{\mathrm{2}} \right)\int_{\mathrm{0}} ^{\infty} \frac{{e}^{−{x}^{\mathrm{2}} } {dx}}{{x}^{\mathrm{2}} +{a}^{\mathrm{2}} }= \\ $$$$=\frac{\sqrt{\pi}}{\mathrm{2}}−\left(\frac{\mathrm{1}}{\mathrm{2}}+{a}^{\mathrm{2}} \right)\int_{\mathrm{0}} ^{\infty} \frac{{e}^{−{x}^{\mathrm{2}} } {dx}}{{x}^{\mathrm{2}} +{a}^{\mathrm{2}} } \\ $$$$\Rightarrow\int_{\mathrm{0}} ^{\infty} \:\frac{{e}^{−{x}^{\mathrm{2}} } }{\left({x}^{\mathrm{2}} +{a}^{\mathrm{2}} \right)^{\mathrm{2}} }{dx}=\frac{\sqrt{\pi}}{\mathrm{2}{a}^{\mathrm{2}} }+\left(\frac{\mathrm{1}}{\mathrm{2}{a}^{\mathrm{2}} }−\mathrm{1}\right)\int_{\mathrm{0}} ^{\infty} \frac{{e}^{−{x}^{\mathrm{2}} } {dx}}{{x}^{\mathrm{2}} +{a}^{\mathrm{2}} } \\ $$

Commented by aleks041103 last updated on 10/Aug/22

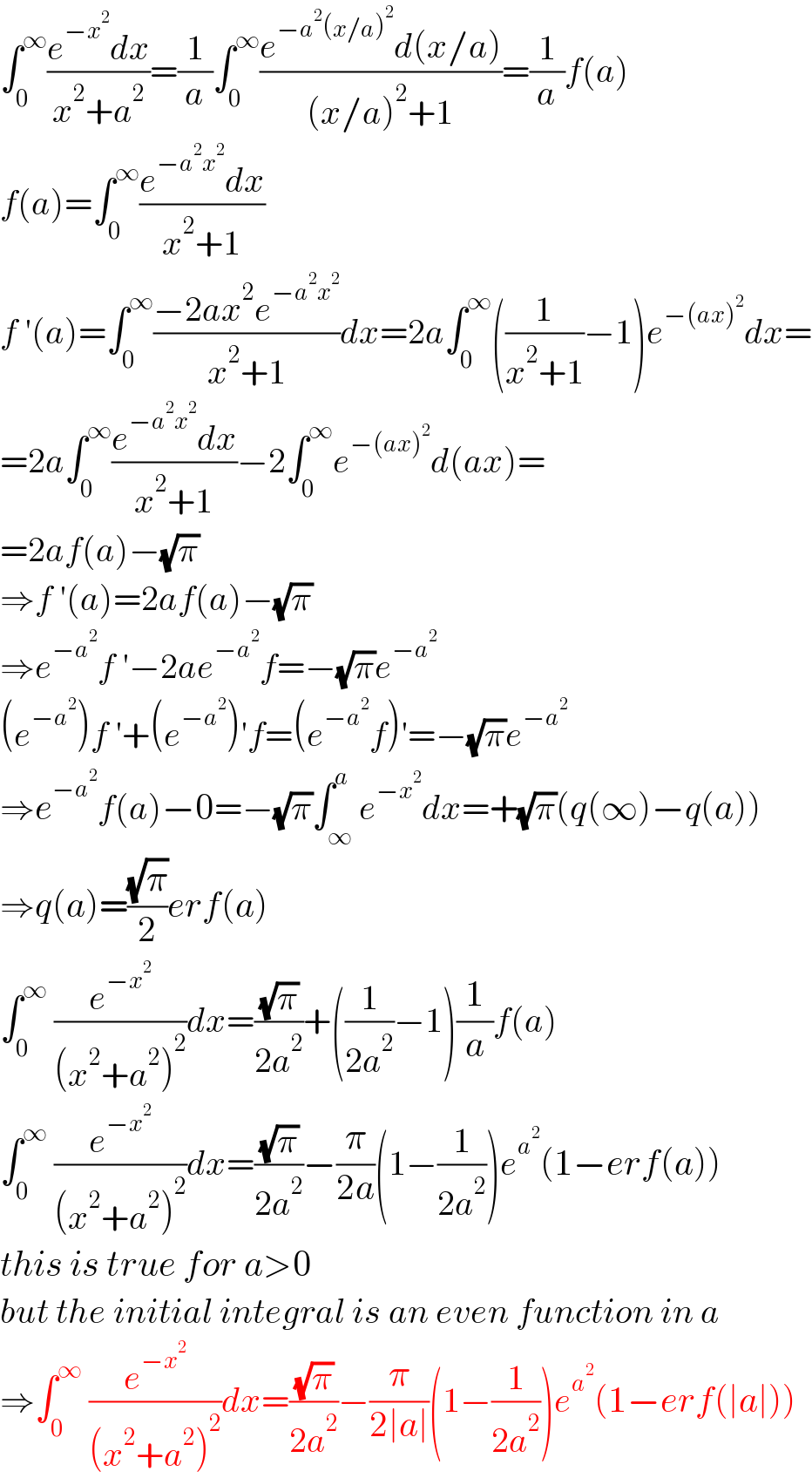
∫_0 ^∞ ((e^(−x^2 ) dx)/(x^2 +a^2 ))=(1/a)∫_0 ^∞ ((e^(−a^2 (x/a)^2 ) d(x/a))/((x/a)^2 +1))=(1/a)f(a) f(a)=∫_0 ^∞ ((e^(−a^2 x^2 ) dx)/(x^2 +1)) f ′(a)=∫_0 ^∞ ((−2ax^2 e^(−a^2 x^2 ) )/(x^2 +1))dx=2a∫_0 ^∞ ((1/(x^2 +1))−1)e^(−(ax)^2 ) dx= =2a∫_0 ^∞ ((e^(−a^2 x^2 ) dx)/(x^2 +1))−2∫_0 ^∞ e^(−(ax)^2 ) d(ax)= =2af(a)−(√π) ⇒f ′(a)=2af(a)−(√π) ⇒e^(−a^2 ) f ′−2ae^(−a^2 ) f=−(√π)e^(−a^2 ) (e^(−a^2 ) )f ′+(e^(−a^2 ) )′f=(e^(−a^2 ) f)′=−(√π)e^(−a^2 ) ⇒e^(−a^2 ) f(a)−0=−(√π)∫_∞ ^a e^(−x^2 ) dx=+(√π)(q(∞)−q(a)) ⇒q(a)=((√π)/2)erf(a) ∫_0 ^∞ (e^(−x^2 ) /((x^2 +a^2 )^2 ))dx=((√π)/(2a^2 ))+((1/(2a^2 ))−1)(1/a)f(a) ∫_0 ^∞ (e^(−x^2 ) /((x^2 +a^2 )^2 ))dx=((√π)/(2a^2 ))−(π/(2a))(1−(1/(2a^2 )))e^a^2 (1−erf(a)) this is true for a>0 but the initial integral is an even function in a ⇒∫_0 ^∞ (e^(−x^2 ) /((x^2 +a^2 )^2 ))dx=((√π)/(2a^2 ))−(π/(2∣a∣))(1−(1/(2a^2 )))e^a^2 (1−erf(∣a∣))

$$\int_{\mathrm{0}} ^{\infty} \frac{{e}^{−{x}^{\mathrm{2}} } {dx}}{{x}^{\mathrm{2}} +{a}^{\mathrm{2}} }=\frac{\mathrm{1}}{{a}}\int_{\mathrm{0}} ^{\infty} \frac{{e}^{−{a}^{\mathrm{2}} \left({x}/{a}\right)^{\mathrm{2}} } {d}\left({x}/{a}\right)}{\left({x}/{a}\right)^{\mathrm{2}} +\mathrm{1}}=\frac{\mathrm{1}}{{a}}{f}\left({a}\right) \\ $$$${f}\left({a}\right)=\int_{\mathrm{0}} ^{\infty} \frac{{e}^{−{a}^{\mathrm{2}} {x}^{\mathrm{2}} } {dx}}{{x}^{\mathrm{2}} +\mathrm{1}} \\ $$$${f}\:'\left({a}\right)=\int_{\mathrm{0}} ^{\infty} \frac{−\mathrm{2}{ax}^{\mathrm{2}} {e}^{−{a}^{\mathrm{2}} {x}^{\mathrm{2}} } }{{x}^{\mathrm{2}} +\mathrm{1}}{dx}=\mathrm{2}{a}\int_{\mathrm{0}} ^{\infty} \left(\frac{\mathrm{1}}{{x}^{\mathrm{2}} +\mathrm{1}}−\mathrm{1}\right){e}^{−\left({ax}\right)^{\mathrm{2}} } {dx}= \\ $$$$=\mathrm{2}{a}\int_{\mathrm{0}} ^{\infty} \frac{{e}^{−{a}^{\mathrm{2}} {x}^{\mathrm{2}} } {dx}}{{x}^{\mathrm{2}} +\mathrm{1}}−\mathrm{2}\int_{\mathrm{0}} ^{\infty} {e}^{−\left({ax}\right)^{\mathrm{2}} } {d}\left({ax}\right)= \\ $$$$=\mathrm{2}{af}\left({a}\right)−\sqrt{\pi} \\ $$$$\Rightarrow{f}\:'\left({a}\right)=\mathrm{2}{af}\left({a}\right)−\sqrt{\pi} \\ $$$$\Rightarrow{e}^{−{a}^{\mathrm{2}} } {f}\:'−\mathrm{2}{ae}^{−{a}^{\mathrm{2}} } {f}=−\sqrt{\pi}{e}^{−{a}^{\mathrm{2}} } \\ $$$$\left({e}^{−{a}^{\mathrm{2}} } \right){f}\:'+\left({e}^{−{a}^{\mathrm{2}} } \right)'{f}=\left({e}^{−{a}^{\mathrm{2}} } {f}\right)'=−\sqrt{\pi}{e}^{−{a}^{\mathrm{2}} } \\ $$$$\Rightarrow{e}^{−{a}^{\mathrm{2}} } {f}\left({a}\right)−\mathrm{0}=−\sqrt{\pi}\int_{\infty} ^{{a}} {e}^{−{x}^{\mathrm{2}} } {dx}=+\sqrt{\pi}\left({q}\left(\infty\right)−{q}\left({a}\right)\right) \\ $$$$\Rightarrow{q}\left({a}\right)=\frac{\sqrt{\pi}}{\mathrm{2}}{erf}\left({a}\right) \\ $$$$\int_{\mathrm{0}} ^{\infty} \:\frac{{e}^{−{x}^{\mathrm{2}} } }{\left({x}^{\mathrm{2}} +{a}^{\mathrm{2}} \right)^{\mathrm{2}} }{dx}=\frac{\sqrt{\pi}}{\mathrm{2}{a}^{\mathrm{2}} }+\left(\frac{\mathrm{1}}{\mathrm{2}{a}^{\mathrm{2}} }−\mathrm{1}\right)\frac{\mathrm{1}}{{a}}{f}\left({a}\right) \\ $$$$\int_{\mathrm{0}} ^{\infty} \:\frac{{e}^{−{x}^{\mathrm{2}} } }{\left({x}^{\mathrm{2}} +{a}^{\mathrm{2}} \right)^{\mathrm{2}} }{dx}=\frac{\sqrt{\pi}}{\mathrm{2}{a}^{\mathrm{2}} }−\frac{\pi}{\mathrm{2}{a}}\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}{a}^{\mathrm{2}} }\right){e}^{{a}^{\mathrm{2}} } \left(\mathrm{1}−{erf}\left({a}\right)\right) \\ $$$${this}\:{is}\:{true}\:{for}\:{a}>\mathrm{0} \\ $$$${but}\:{the}\:{initial}\:{integral}\:{is}\:{an}\:{even}\:{function}\:{in}\:{a} \\ $$$$\Rightarrow\int_{\mathrm{0}} ^{\infty} \:\frac{{e}^{−{x}^{\mathrm{2}} } }{\left({x}^{\mathrm{2}} +{a}^{\mathrm{2}} \right)^{\mathrm{2}} }{dx}=\frac{\sqrt{\pi}}{\mathrm{2}{a}^{\mathrm{2}} }−\frac{\pi}{\mathrm{2}\mid{a}\mid}\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}{a}^{\mathrm{2}} }\right){e}^{{a}^{\mathrm{2}} } \left(\mathrm{1}−{erf}\left(\mid{a}\mid\right)\right) \\ $$

Commented by princeDera last updated on 10/Aug/22