Question Number 152653 by mnjuly1970 last updated on 30/Aug/21
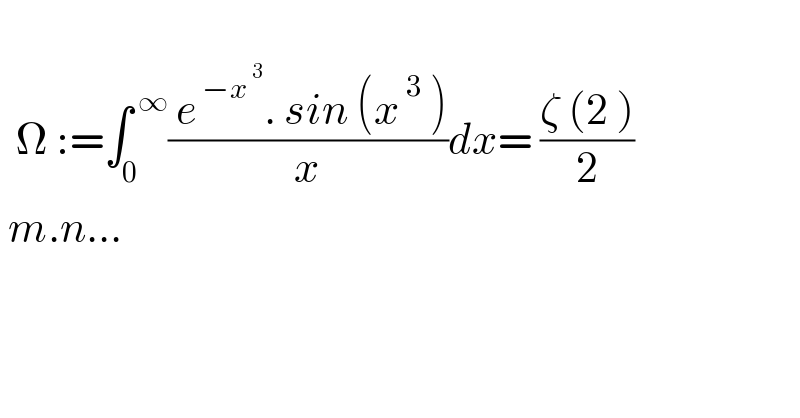
$$ \\ $$$$\:\:\Omega\::=\int_{\mathrm{0}} ^{\:\infty} \frac{\:{e}^{\:−{x}^{\:\mathrm{3}} } .\:{sin}\:\left({x}^{\:\mathrm{3}} \:\right)}{{x}}{dx}=\:\frac{\zeta\:\left(\mathrm{2}\:\right)}{\mathrm{2}} \\ $$$$\:{m}.{n}… \\ $$$$ \\ $$
Answered by qaz last updated on 30/Aug/21
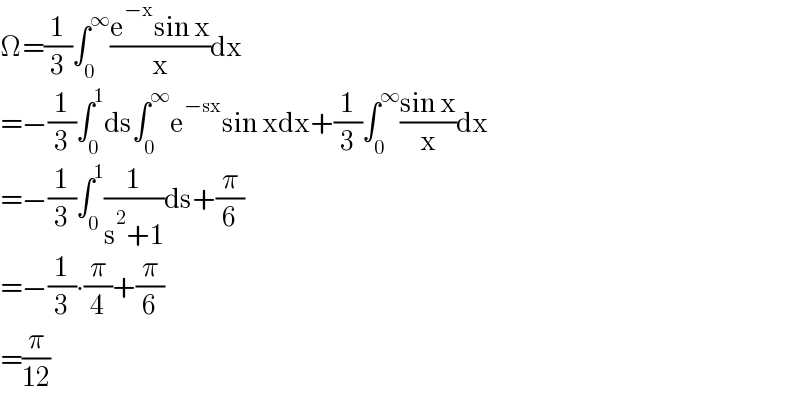
$$\Omega=\frac{\mathrm{1}}{\mathrm{3}}\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{e}^{−\mathrm{x}} \mathrm{sin}\:\mathrm{x}}{\mathrm{x}}\mathrm{dx} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{3}}\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{ds}\int_{\mathrm{0}} ^{\infty} \mathrm{e}^{−\mathrm{sx}} \mathrm{sin}\:\mathrm{xdx}+\frac{\mathrm{1}}{\mathrm{3}}\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{sin}\:\mathrm{x}}{\mathrm{x}}\mathrm{dx} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{3}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}}{\mathrm{s}^{\mathrm{2}} +\mathrm{1}}\mathrm{ds}+\frac{\pi}{\mathrm{6}} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{3}}\centerdot\frac{\pi}{\mathrm{4}}+\frac{\pi}{\mathrm{6}} \\ $$$$=\frac{\pi}{\mathrm{12}} \\ $$
