Menu Close

0-e-x-7-sin-x-7-dx-

Tinku Tara 0 Comments
Pin




Question Number 124461 by Dwaipayan Shikari last updated on 03/Dec/20
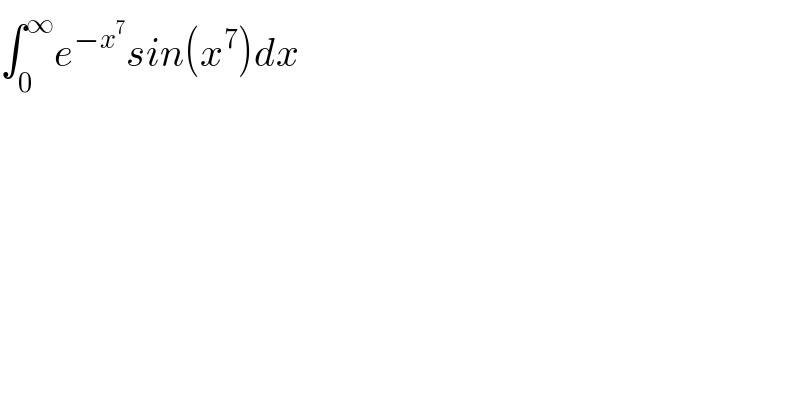
∫_0 ^∞ e^(−x^7 ) sin(x^7 )dx
$$\int_{\mathrm{0}} ^{\infty} {e}^{−{x}^{\mathrm{7}} } {sin}\left({x}^{\mathrm{7}} \right){dx} \\ $$
Commented by Dwaipayan Shikari last updated on 03/Dec/20
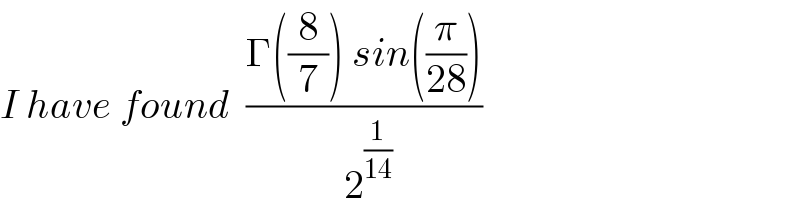
I have found ((Γ((8/7)) sin((π/(28))))/( 2^(1/(14)) ))
$${I}\:{have}\:{found}\:\:\frac{\Gamma\left(\frac{\mathrm{8}}{\mathrm{7}}\right)\:{sin}\left(\frac{\pi}{\mathrm{28}}\right)}{\:\mathrm{2}^{\frac{\mathrm{1}}{\mathrm{14}}} } \\ $$
Commented by Dwaipayan Shikari last updated on 03/Dec/20
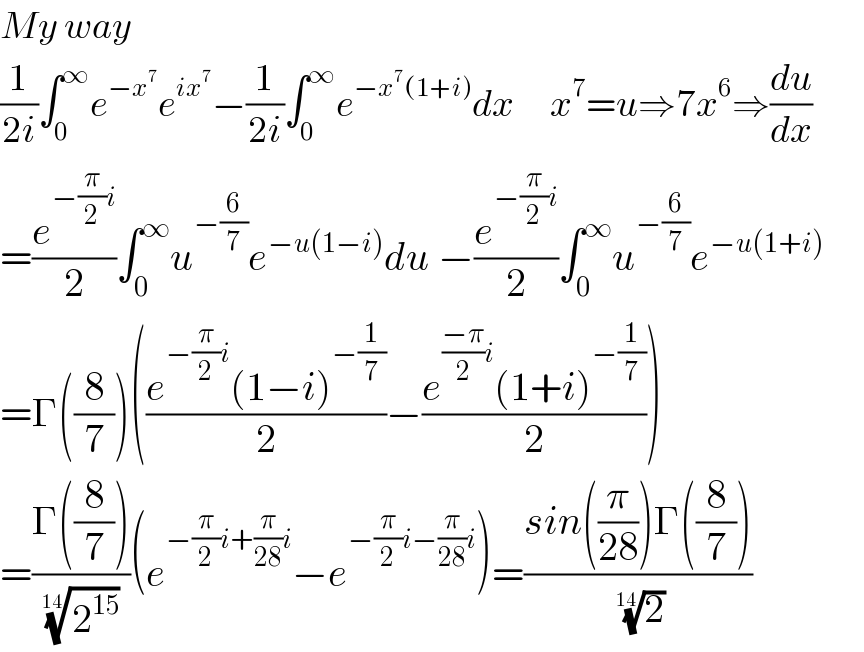
My way (1/(2i))∫_0 ^∞ e^(−x^7 ) e^(ix^7 ) −(1/(2i))∫_0 ^∞ e^(−x^7 (1+i)) dx x^7 =u⇒7x^6 ⇒(du/dx) =(e^(−(π/2)i) /2)∫_0 ^∞ u^(−(6/7)) e^(−u(1−i)) du −(e^(−(π/2)i) /2)∫_0 ^∞ u^(−(6/7)) e^(−u(1+i)) =Γ((8/7))(((e^(−(π/2)i) (1−i)^(−(1/7)) )/2)−((e^(((−π)/2)i) (1+i)^(−(1/7)) )/2)) =((Γ((8/7)))/( (2^(15) )^(1/(14)) ))(e^(−(π/2)i+(π/(28))i) −e^(−(π/2)i−(π/(28))i) )=((sin((π/(28)))Γ((8/7)))/( (2)^(1/(14)) ))
$${My}\:{way} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}{i}}\int_{\mathrm{0}} ^{\infty} {e}^{−{x}^{\mathrm{7}} } {e}^{{ix}^{\mathrm{7}} } −\frac{\mathrm{1}}{\mathrm{2}{i}}\int_{\mathrm{0}} ^{\infty} {e}^{−{x}^{\mathrm{7}} \left(\mathrm{1}+{i}\right)} {dx}\:\:\:\:\:\:{x}^{\mathrm{7}} ={u}\Rightarrow\mathrm{7}{x}^{\mathrm{6}} \Rightarrow\frac{{du}}{{dx}} \\ $$$$=\frac{{e}^{−\frac{\pi}{\mathrm{2}}{i}} }{\mathrm{2}}\int_{\mathrm{0}} ^{\infty} {u}^{−\frac{\mathrm{6}}{\mathrm{7}}} {e}^{−{u}\left(\mathrm{1}−{i}\right)} {du}\:−\frac{{e}^{−\frac{\pi}{\mathrm{2}}{i}} }{\mathrm{2}}\int_{\mathrm{0}} ^{\infty} {u}^{−\frac{\mathrm{6}}{\mathrm{7}}} {e}^{−{u}\left(\mathrm{1}+{i}\right)} \:\:\:\:\: \\ $$$$=\Gamma\left(\frac{\mathrm{8}}{\mathrm{7}}\right)\left(\frac{{e}^{−\frac{\pi}{\mathrm{2}}{i}} \left(\mathrm{1}−{i}\right)^{−\frac{\mathrm{1}}{\mathrm{7}}} }{\mathrm{2}}−\frac{{e}^{\frac{−\pi}{\mathrm{2}}{i}} \left(\mathrm{1}+{i}\right)^{−\frac{\mathrm{1}}{\mathrm{7}}} }{\mathrm{2}}\right) \\ $$$$=\frac{\Gamma\left(\frac{\mathrm{8}}{\mathrm{7}}\right)}{\:\sqrt[{\mathrm{14}}]{\mathrm{2}^{\mathrm{15}} }}\left({e}^{−\frac{\pi}{\mathrm{2}}{i}+\frac{\pi}{\mathrm{28}}{i}} −{e}^{−\frac{\pi}{\mathrm{2}}{i}−\frac{\pi}{\mathrm{28}}{i}} \right)=\frac{{sin}\left(\frac{\pi}{\mathrm{28}}\right)\Gamma\left(\frac{\mathrm{8}}{\mathrm{7}}\right)}{\:\sqrt[{\mathrm{14}}]{\mathrm{2}}} \\ $$
Answered by mnjuly1970 last updated on 03/Dec/20
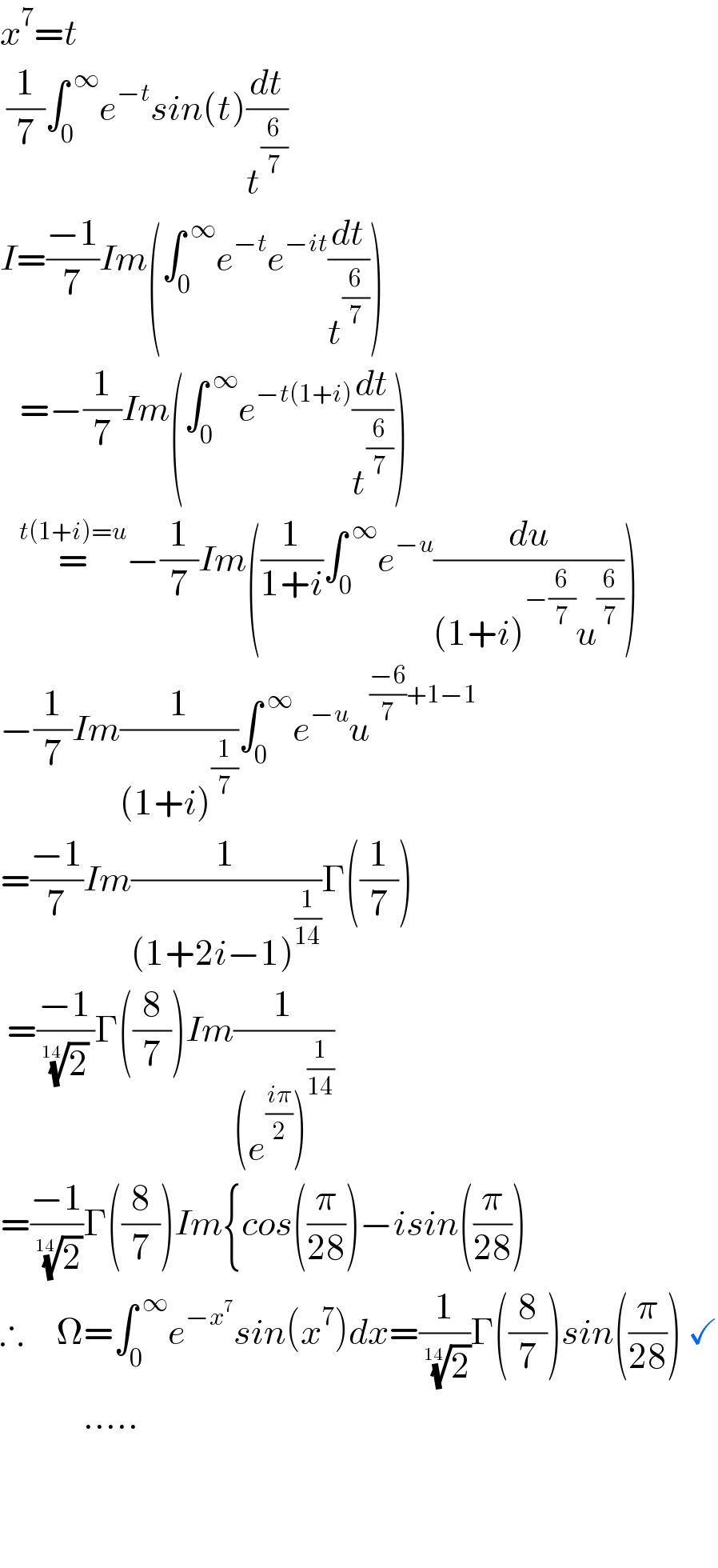
x^7 =t (1/7)∫_0 ^( ∞) e^(−t) sin(t)(dt/t^(6/7) ) I=((−1)/7)Im(∫_0 ^( ∞) e^(−t) e^(−it) (dt/t^(6/7) )) =−(1/7)Im(∫_(0 ) ^( ∞) e^(−t(1+i)) (dt/t^(6/7) )) =^(t(1+i)=u) −(1/7)Im((1/(1+i))∫_0 ^( ∞) e^(−u) (du/((1+i)^(−(6/7)) u^(6/7) ))) −(1/7)Im(1/((1+i)^(1/7) ))∫_0 ^( ∞) e^(−u) u^(((−6)/7)+1−1) =((−1)/7)Im(1/((1+2i−1)^(1/(14)) ))Γ((1/7)) =((−1)/( (2)^(1/(14)) ))Γ((8/7))Im(1/((e^((iπ)/2) )^(1/(14)) )) =((−1)/( (2)^(1/(14)) ))Γ((8/7))Im{cos((π/(28)))−isin((π/(28))) ∴ Ω=∫_0 ^( ∞) e^(−x^7 ) sin(x^7 )dx=(1/( (2)^(1/(14)) ))Γ((8/7))sin((π/(28))) ✓ .....
$${x}^{\mathrm{7}} ={t} \\ $$$$\:\frac{\mathrm{1}}{\mathrm{7}}\int_{\mathrm{0}} ^{\:\infty} {e}^{−{t}} {sin}\left({t}\right)\frac{{dt}}{{t}^{\frac{\mathrm{6}}{\mathrm{7}}} } \\ $$$${I}=\frac{−\mathrm{1}}{\mathrm{7}}{Im}\left(\int_{\mathrm{0}} ^{\:\infty} {e}^{−{t}} {e}^{−{it}} \frac{{dt}}{{t}^{\frac{\mathrm{6}}{\mathrm{7}}} }\right) \\ $$$$\:\:\:=−\frac{\mathrm{1}}{\mathrm{7}}{Im}\left(\int_{\mathrm{0}\:} ^{\:\infty} {e}^{−{t}\left(\mathrm{1}+{i}\right)} \frac{{dt}}{{t}^{\frac{\mathrm{6}}{\mathrm{7}}} }\right) \\ $$$$\:\:\:\overset{{t}\left(\mathrm{1}+{i}\right)={u}} {=}−\frac{\mathrm{1}}{\mathrm{7}}{Im}\left(\frac{\mathrm{1}}{\mathrm{1}+{i}}\int_{\mathrm{0}} ^{\:\infty} {e}^{−{u}} \frac{{du}}{\left(\mathrm{1}+{i}\right)^{−\frac{\mathrm{6}}{\mathrm{7}}} {u}^{\frac{\mathrm{6}}{\mathrm{7}}} }\right) \\ $$$$−\frac{\mathrm{1}}{\mathrm{7}}{Im}\frac{\mathrm{1}}{\left(\mathrm{1}+{i}\right)^{\frac{\mathrm{1}}{\mathrm{7}}} }\int_{\mathrm{0}} ^{\:\infty} {e}^{−{u}} {u}^{\frac{−\mathrm{6}}{\mathrm{7}}+\mathrm{1}−\mathrm{1}} \\ $$$$=\frac{−\mathrm{1}}{\mathrm{7}}{Im}\frac{\mathrm{1}}{\left(\mathrm{1}+\mathrm{2}{i}−\mathrm{1}\right)^{\frac{\mathrm{1}}{\mathrm{14}}} }\Gamma\left(\frac{\mathrm{1}}{\mathrm{7}}\right) \\ $$$$\:=\frac{−\mathrm{1}}{\:\sqrt[{\mathrm{14}}]{\mathrm{2}}\:}\Gamma\left(\frac{\mathrm{8}}{\mathrm{7}}\right){Im}\frac{\mathrm{1}}{\left({e}^{\frac{{i}\pi}{\mathrm{2}}} \right)^{\frac{\mathrm{1}}{\mathrm{14}}} } \\ $$$$=\frac{−\mathrm{1}}{\:\sqrt[{\mathrm{14}}]{\mathrm{2}}}\Gamma\left(\frac{\mathrm{8}}{\mathrm{7}}\right){Im}\left\{{cos}\left(\frac{\pi}{\mathrm{28}}\right)−{isin}\left(\frac{\pi}{\mathrm{28}}\right)\right. \\ $$$$\therefore\:\:\:\:\:\Omega=\int_{\mathrm{0}} ^{\:\infty} {e}^{−{x}^{\mathrm{7}} } {sin}\left({x}^{\mathrm{7}} \right){dx}=\frac{\mathrm{1}}{\:\sqrt[{\mathrm{14}}]{\mathrm{2}}}\Gamma\left(\frac{\mathrm{8}}{\mathrm{7}}\right){sin}\left(\frac{\pi}{\mathrm{28}}\right)\:\checkmark \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:…..\: \\ $$$$\:\: \\ $$$$ \\ $$
Commented by Dwaipayan Shikari last updated on 03/Dec/20
Thanking you
$${Thanking}\:{you} \\ $$
Commented by mnjuly1970 last updated on 03/Dec/20
grateful your questions are very stunning..
$${grateful} \\ $$$${your}\:{questions}\:{are}\:{very}\:{stunning}.. \\ $$
Answered by mathmax by abdo last updated on 03/Dec/20
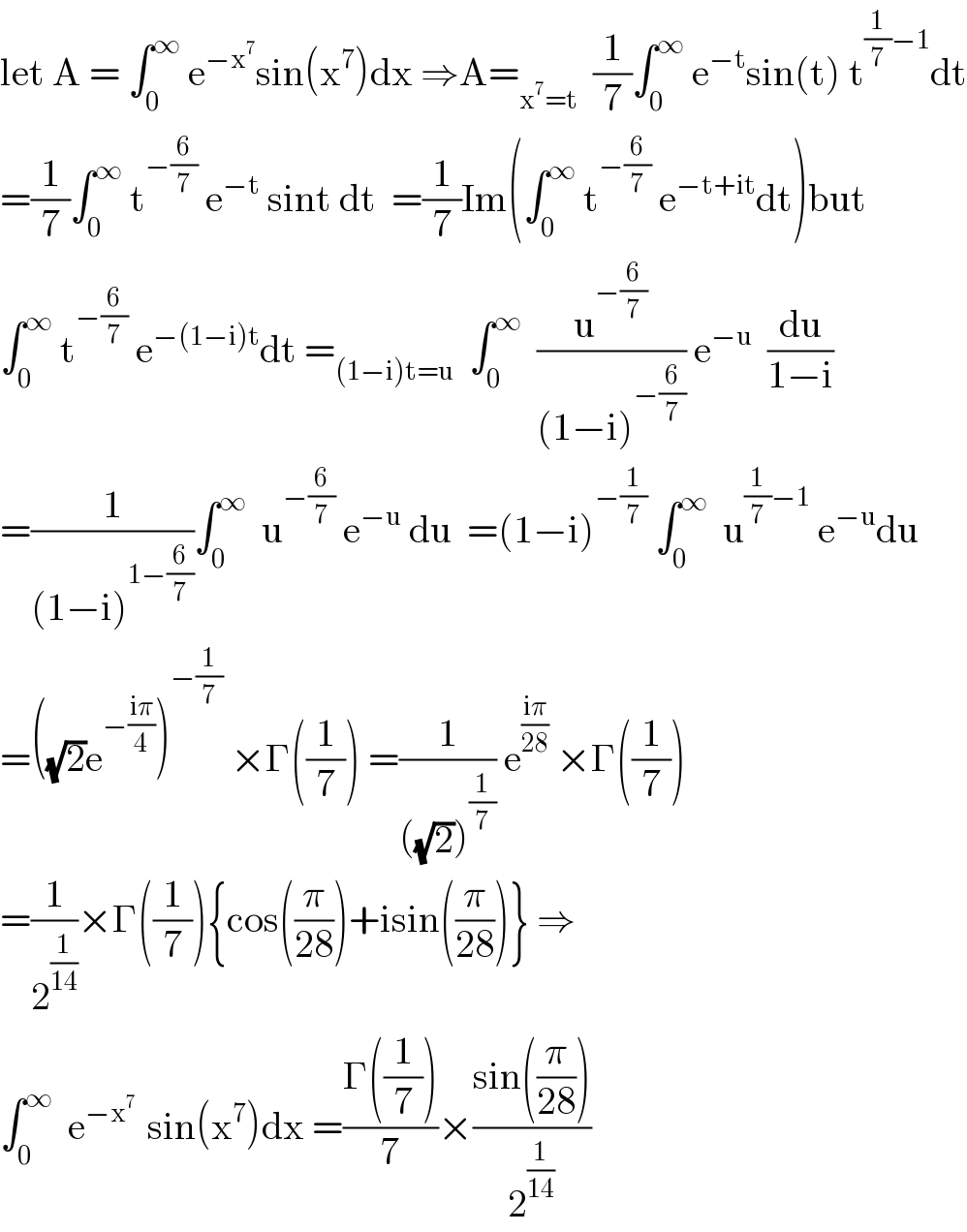
let A = ∫_0 ^∞ e^(−x^7 ) sin(x^7 )dx ⇒A=_(x^7 =t) (1/7)∫_0 ^∞ e^(−t) sin(t) t^((1/7)−1) dt =(1/7)∫_0 ^∞ t^(−(6/7)) e^(−t) sint dt =(1/7)Im(∫_0 ^∞ t^(−(6/7)) e^(−t+it) dt)but ∫_0 ^∞ t^(−(6/7)) e^(−(1−i)t) dt =_((1−i)t=u) ∫_0 ^∞ (u^(−(6/7)) /((1−i)^(−(6/7)) )) e^(−u) (du/(1−i)) =(1/((1−i)^(1−(6/7)) ))∫_0 ^∞ u^(−(6/7)) e^(−u) du =(1−i)^(−(1/7)) ∫_0 ^∞ u^((1/7)−1) e^(−u) du =((√2)e^(−((iπ)/4)) )^(−(1/7)) ×Γ((1/7)) =(1/(((√2))^(1/7) )) e^((iπ)/(28)) ×Γ((1/7)) =(1/2^(1/(14)) )×Γ((1/7)){cos((π/(28)))+isin((π/(28)))} ⇒ ∫_0 ^∞ e^(−x^7 ) sin(x^7 )dx =((Γ((1/7)))/7)×((sin((π/(28))))/2^(1/(14)) )
$$\mathrm{let}\:\mathrm{A}\:=\:\int_{\mathrm{0}} ^{\infty} \:\mathrm{e}^{−\mathrm{x}^{\mathrm{7}} } \mathrm{sin}\left(\mathrm{x}^{\mathrm{7}} \right)\mathrm{dx}\:\Rightarrow\mathrm{A}=_{\mathrm{x}^{\mathrm{7}} =\mathrm{t}} \:\:\frac{\mathrm{1}}{\mathrm{7}}\int_{\mathrm{0}} ^{\infty} \:\mathrm{e}^{−\mathrm{t}} \mathrm{sin}\left(\mathrm{t}\right)\:\mathrm{t}^{\frac{\mathrm{1}}{\mathrm{7}}−\mathrm{1}} \mathrm{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{7}}\int_{\mathrm{0}} ^{\infty} \:\mathrm{t}^{−\frac{\mathrm{6}}{\mathrm{7}}} \:\mathrm{e}^{−\mathrm{t}} \:\mathrm{sint}\:\mathrm{dt}\:\:=\frac{\mathrm{1}}{\mathrm{7}}\mathrm{Im}\left(\int_{\mathrm{0}} ^{\infty} \:\mathrm{t}^{−\frac{\mathrm{6}}{\mathrm{7}}} \:\mathrm{e}^{−\mathrm{t}+\mathrm{it}} \mathrm{dt}\right)\mathrm{but} \\ $$$$\int_{\mathrm{0}} ^{\infty} \:\mathrm{t}^{−\frac{\mathrm{6}}{\mathrm{7}}} \:\mathrm{e}^{−\left(\mathrm{1}−\mathrm{i}\right)\mathrm{t}} \mathrm{dt}\:=_{\left(\mathrm{1}−\mathrm{i}\right)\mathrm{t}=\mathrm{u}} \:\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{u}^{−\frac{\mathrm{6}}{\mathrm{7}}} }{\left(\mathrm{1}−\mathrm{i}\right)^{−\frac{\mathrm{6}}{\mathrm{7}}} }\:\mathrm{e}^{−\mathrm{u}} \:\:\frac{\mathrm{du}}{\mathrm{1}−\mathrm{i}} \\ $$$$=\frac{\mathrm{1}}{\left(\mathrm{1}−\mathrm{i}\right)^{\mathrm{1}−\frac{\mathrm{6}}{\mathrm{7}}} }\int_{\mathrm{0}} ^{\infty} \:\:\mathrm{u}^{−\frac{\mathrm{6}}{\mathrm{7}}} \:\mathrm{e}^{−\mathrm{u}} \:\mathrm{du}\:\:=\left(\mathrm{1}−\mathrm{i}\right)^{−\frac{\mathrm{1}}{\mathrm{7}}} \:\int_{\mathrm{0}} ^{\infty} \:\:\mathrm{u}^{\frac{\mathrm{1}}{\mathrm{7}}−\mathrm{1}} \:\mathrm{e}^{−\mathrm{u}} \mathrm{du} \\ $$$$=\left(\sqrt{\mathrm{2}}\mathrm{e}^{−\frac{\mathrm{i}\pi}{\mathrm{4}}} \right)^{−\frac{\mathrm{1}}{\mathrm{7}}} \:×\Gamma\left(\frac{\mathrm{1}}{\mathrm{7}}\right)\:=\frac{\mathrm{1}}{\left(\sqrt{\mathrm{2}}\right)^{\frac{\mathrm{1}}{\mathrm{7}}} }\:\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{28}}} \:×\Gamma\left(\frac{\mathrm{1}}{\mathrm{7}}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}^{\frac{\mathrm{1}}{\mathrm{14}}} }×\Gamma\left(\frac{\mathrm{1}}{\mathrm{7}}\right)\left\{\mathrm{cos}\left(\frac{\pi}{\mathrm{28}}\right)+\mathrm{isin}\left(\frac{\pi}{\mathrm{28}}\right)\right\}\:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\infty} \:\:\mathrm{e}^{−\mathrm{x}^{\mathrm{7}} \:} \:\mathrm{sin}\left(\mathrm{x}^{\mathrm{7}} \right)\mathrm{dx}\:=\frac{\Gamma\left(\frac{\mathrm{1}}{\mathrm{7}}\right)}{\mathrm{7}}×\frac{\mathrm{sin}\left(\frac{\pi}{\mathrm{28}}\right)}{\mathrm{2}^{\frac{\mathrm{1}}{\mathrm{14}}} } \\ $$
Commented by mathmax by abdo last updated on 03/Dec/20
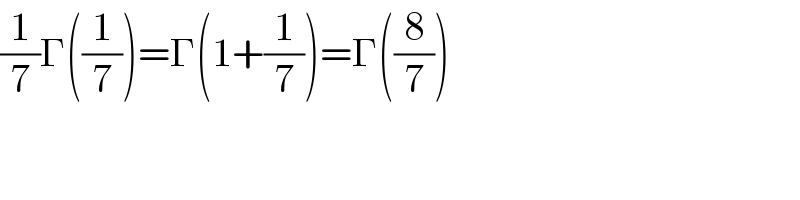
(1/7)Γ((1/7))=Γ(1+(1/7))=Γ((8/7))
$$\frac{\mathrm{1}}{\mathrm{7}}\Gamma\left(\frac{\mathrm{1}}{\mathrm{7}}\right)=\Gamma\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{7}}\right)=\Gamma\left(\frac{\mathrm{8}}{\mathrm{7}}\right) \\ $$
Commented by Dwaipayan Shikari last updated on 03/Dec/20
Thanking you
$${Thanking}\:{you} \\ $$
Commented by mathmax by abdo last updated on 03/Dec/20
you are welcome
$$\mathrm{you}\:\mathrm{are}\:\mathrm{welcome} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *